本文已参与[新人创作礼]活动,一起开启掘金创作之路

转载请注明出处.

图形学的数学基础（三十五）：法线变换

你可能会问为什么不简单地把法线看作向量。为什么要将他们区别对待呢?在前几章中，我们已经学习了使用矩阵乘法来变换点和向量。法线的问题是，当矩阵对法线进行均匀缩放时，这样做没问题。但是现在让我们考虑一下将非均匀缩放应用到一个物体上的情况。让我们(在2D中)画一条经过点a =(0,1,0)和点B=(1,0,0)的直线，然后从原点到坐标(1,1,0)再画一条直线，你会发现这条直线垂直于我们的平面。假设(1,1,0)是$AB$的法线.

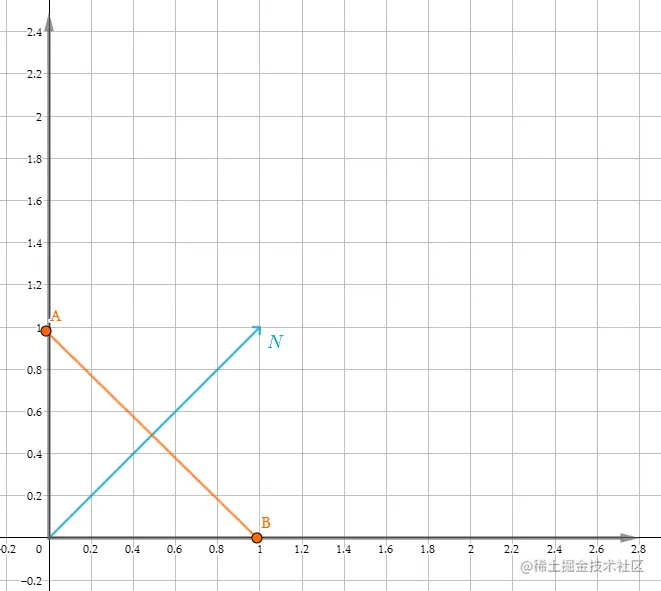
现在假设我们使用以下矩阵对平面应用非均匀缩放:

$\textbf{M} = \begin{bmatrix} 2&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix}$

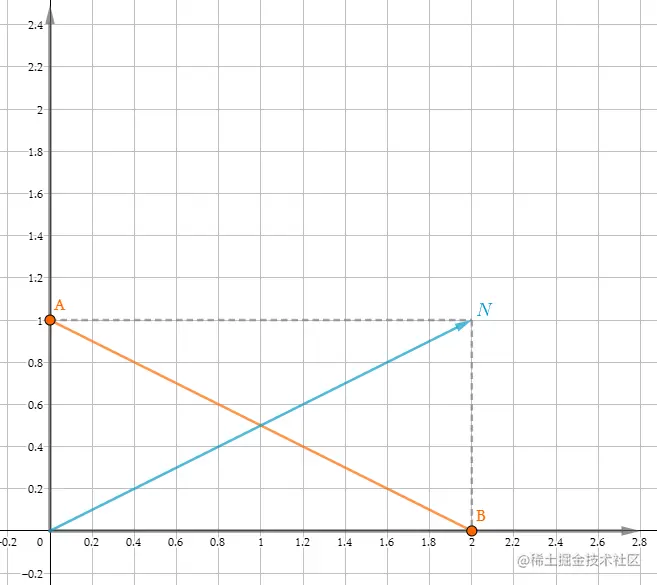
在对$AB$和$\vec{N}$应用同样的变换矩阵$M$后,我们发现之前垂直的两条线不再垂直了,这也从侧面说明,对法线直接应用Model矩阵结果是错误的。实际上变换法线不能直接应用和变换顶点相同的矩阵M，而需要应用其逆矩阵的转置。

$\vec{N^丶} = \textbf{M}^{-1T}\vec{N}$

在进行数学推导之前，先让我们从直觉上进行解释。首先法线代表方向，是一个矢量，因此平移矩阵不会对其产生影响，因为矢量的w分量为0，换句话说对于一个4x4的矩阵M，我们可以忽略第四行和第四列，只考虑左上角3x3的部分（缩放和旋转）。我们将3x3的矩阵分解为两部分看待，分别为旋转和缩放。我们都知道旋转矩阵是正交矩阵，而正交矩阵的逆等于其转置，因此对于旋转矩阵$R$来说：

$R^T =R^{-1}$

$R = R^{-1T}$

旋转矩阵逆矩阵的转置等于其自身。

对于缩放的部分，缩放矩阵的转置等于其自身，缩放矩阵的逆可以很容易的通过其缩放因子计算：

$M^{-1T} = \begin{bmatrix} 1/2&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix}$

对上图中的$\vec{N}$应用该矩阵：

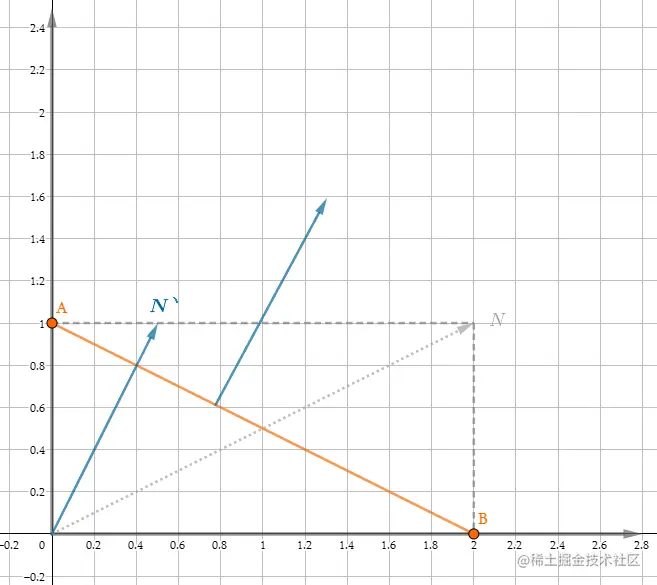
数学推导：

首先澄清几个概念:

• 两个正交向量的点积等于0
• 两个向量的点积可以写成1x3和3x1矩阵乘积的形式
• 如果两个向量点乘结果为0，则对应的矩阵乘积形式结果也为0

$\textbf{v}\cdot\textbf{n} = \begin{bmatrix} v_x&v_y&v_z \end{bmatrix}\begin{bmatrix} n_x\\ n_y\\ n_z\\ \end{bmatrix} = \textbf{v} * \textbf{n}^T = 0$

$\textbf{v}\cdot\textbf{n} = \textbf{v} * \textbf{n}^T = v_x*n_x + v_y*n_y + v_z*n_z$

$\textbf{v}*\textbf{n}^T = \textbf{v}* M * M^{-1} * \textbf{n}^T$

根据矩阵转置的性质：$(AB)^T = B^TA^T$可以推导出：

$\textbf{v}*\textbf{n}^T = (\textbf{v}* M)*(\textbf{n}*M^{-1T})^T$

注意观察以上表达式，我们注意到等号右侧第一个括号内的$\textbf{v}*M$,实际上是原始顶点$v$在经过矩阵M变换后得到的$v^丶$:

$\textbf{v}^丶 = \textbf{v}*M$

我们知道两个向量在经过变换后仍然得保持垂直，因此：

$\textbf{v}*\textbf{n}^T = \textbf{v}^丶*\textbf{n}^{丶T} = 0$

因此，等号右侧的第二部分$(\textbf{n}*M^{-1T})^T$可以重写为：

$\textbf{n}^{丶T} = (\textbf{n}*M^{-1T})^T$

$\textbf{n}^丶 = \textbf{n}*M^{-1T}$

也就是说$\textbf{n}$只有经过$M^{-1T}$变换后才能成为$\textbf{n}^丶$，才能做到变换后依然和$v^丶$垂直。

参考

用一篇文章理解法线变换、切线空间、法线贴图

切线空间（Tangent Space）完全解析

RealTime Rendering

learningOpenGL

GAMES101

scratchapixel