本文已参与「新人创作礼」活动，一起开启掘金创作之路。

1. 时间复杂度

1.1. 概念描述

为了解决时间分析的难题，有了渐进时间复杂度(asymptotic time complexity) 的概念，其官方定义如下：

算法中基本操作重复执行的次数是问题规模 $n$ 的某个函数，用 $T(n)$ 表示；若存在函数 $f(n)$，使得当 $n$ 趋近于无穷大时，$T(n)/f(n)$ 的极限值为不等于零的常数，则称 $f(n)$ 是 $T(n)$ 的同数量级函数。记作 $T(n)=O(f(n))$，称为 $O(f(n))$，$O$ 为算法的渐进时间复杂度，简称为时间复杂度。也被称为大 O 表示法。大 O 表示法可以告诉我们算法的快慢。

大 O 表示法就是将算法的所有步骤转换为代数项，然后排除不会对问题的整体复杂度产生较大影响的较低阶常数和系数。

大 O 表示法比较的是操作数，它指出了算法运行时间的增速。$O(n)$ 括号里的是操作数。

1.2. 示例说明

大 O 表示法指出了最糟情况下的运行时间。因此，大 O 表示法就是把程序的相对执行时间函数 $T(n)$ 简化为一个数量级，这个数量级可以是 $n$、$n^2$、$n^3$ 等，原则如下：

• 如果运行时间是常数量级，则用常数 1 表示。
• 只保留时间函数中的最高阶项。
• 如果最高阶项存在，则省去最高阶项前面的系数。

示例：

$T(n) = 3n$ 最高阶项为 $3n$，省去系数 $3$，则转化的时间复杂度为：$T(n)=O(n)$。

$T(n) = 5\log n$，最高阶项为 $5\log n$，省去系数 $5$，则转化的时间复杂度为：$T(n) =O(\log n)$。

$T(n) = 2$，只有常数量级，则转化的时间复杂度为：$T(n) =O(1)$。

$T(n) = 0.5n^2+ 0.5n$，最高阶项为 $0.5n^2$，省去系数 $0.5$，则转化的时间复杂度为：$T(n)=O(n^2)$。

这 4 种时间复杂度排序：

$O(1)<O(\log n)<O(n)<O(n^2)$

1.3. 常见复杂度

复杂度	量级	例子
$O(1)$	常量阶
$O(\log n)$	对数阶	二分查找
$O(n)$	线性阶	简单查找
$O(n\log n)$	线性对数阶	快速排序
$O(n^2)、O(n^3) ... O(n^k)$	平方阶、立方阶 ... K次方阶	选择排序、冒泡排序（平方阶）
$O(2^n)$	指数阶	汉诺塔问题
$O(n!)$	阶乘阶	旅行商问题

根据复杂度量级，可以分为两类：多项式量级和非多项式量级，非多项式量级的只有 $O(2^n)$ 和 $O(n!)$。当数据规模 $n$ 越来越大时候，非多项式量级算法的执行时间增长很快，所以效率比较低。

以下是几种常见的多项式量级的时间复杂度：

O(1)

只要代码的执行时间不随 $n$ 的增大而增长，这样代码的时间复杂度我们都记作 $O(1)$。或者说，一般情况下，只要算法中不存在循环语句、递归语句，即使有成千上万行的代码，其时间复杂度也是 $Ο(1)$。

O(log n)、O(nlog n)

不论是 2 为底还是以 3 为底，还是以 10 为底，我们都可以把所有对数阶的时间复杂度记为 $O(\log n)$，为什么呢？

因为对数之间是可以互相转换的，$\log_3 n$ 就等于 $\log_32 * \log_2n$，所以 $O(\log_3n) = O(C * \log_2n)$，其中 $C=\log_32$ 是一个常量。而采用大 O 表示法标记复杂度的时候，可以忽略系数，所以 在对数的时间复杂度表示方法里，可以忽略对数的底，统一表示为 $O(\log n)$。

将时间复杂度为 $O(\log n)$ 的代码循环 $n$ 遍的话，时间复杂度就是 $O(n\log n)$。

O(m+n)、O(m*n)

此时代码的复杂度由两个数据的规模决定，事先无法评估 $m$ 和 $n$ 谁的量级大，所以没办法省略哪一个。

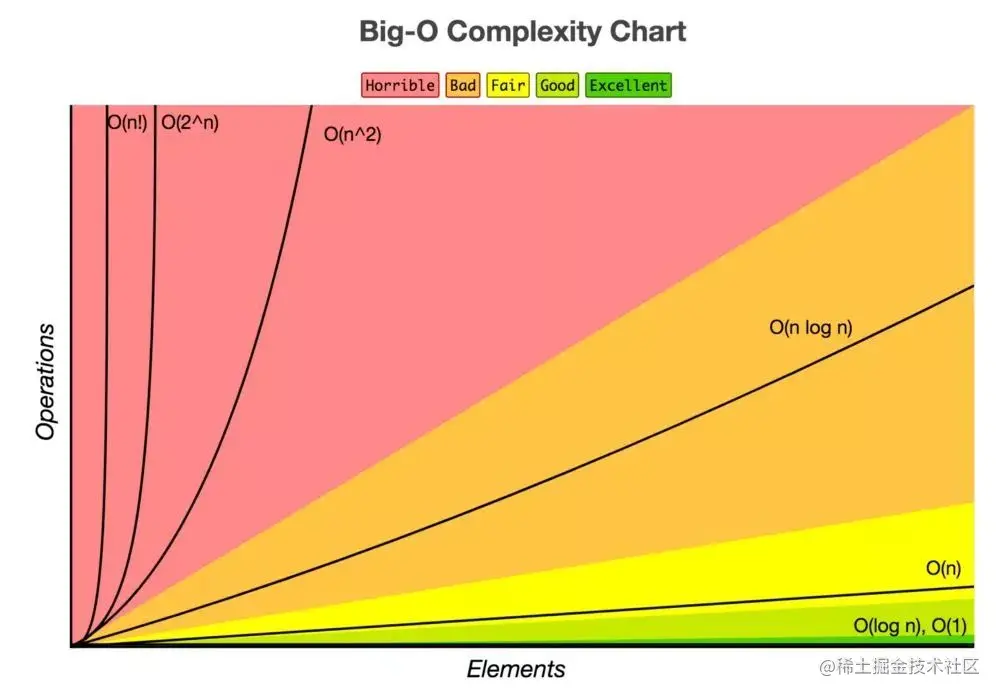
常见算法复杂度样例

2. 空间复杂度

空间复杂度(SpaceComplexity) 是对一个算法在运行过程中临时占用存储空间大小的一个度量，同样反映的是一个趋势，我们用 $S(n)$ 来定义，关心算法需要的额外空间。

在电子计算机时代的早期，时间和空间这两种资源都是极其昂贵的。但是经过几十年不懈的技术革新，计算机的速度和存储容量已经提高了好几个数量级。现在，一个算法所需要的额外空间，往往已经不是我们关注的重点问题了。因此现阶段算法重点关注的是时间复杂度。

空间复杂度比较常用的有：$O(1)$、$O(n)$。

如果算法执行所需要的临时空间不随着某个变量 $n$ 的大小而变化，即此算法空间复杂度为一个常量，可表示为 $S(n)=O(1)$。

如果算法执行所需要的临时空间随着某个变量 $n$ 的大小而线性变化，则此算法空间复杂度可表示为 $S(n)=O(n)$。

3. 常用数学公式

3.1. 指数

3.2. 对数

在计算机科学中，除非有特别的声明，否则所有的对数都是以 2 为底的。

定义：$X^A=B$ 当且仅当 $\log_XB=A$ 。由该定义可得到下面几个方便的等式：

$\log X \lt X$ 对所有的 $X \gt 0$ 成立。

$\log1=0, \quad \log2=1, \quad \log1024=10, \quad \log1048576=20$