基础知识

角度弧度换算

用弧度度量的角 = π/180 × 用度度量的角

用角度度量的角 = 180/π × 用弧度度量的角

sin cos tan csc sec cot

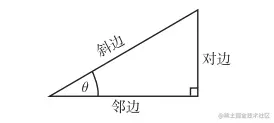
sin(θ) = 对边/斜边

cos(θ) = 临边/斜边

tan(θ) = 对边/临边 = sin(θ)/cos(θ)

csc(θ) = 1/sin(θ)

sec(θ) = 1/cos(θ)

cot(θ) = 1/tan(θ)

常用三角函数速记表

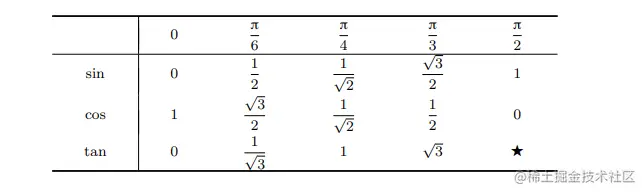
计算三角函数

参考角

θ 的参考角是在表示角 θ 的射线和 x 轴之间的最小的角, 它必定介于 0 到 π/2之间

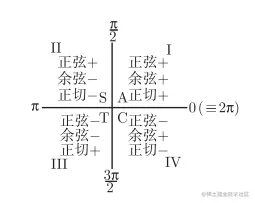
ASTC表示法

三角恒等式

$sin(θ)^2 + cos(θ)^2 = 1$

$1 + tan(θ)^2 = sec(θ)^2$

$cot(θ)^2 + 1 = csc(θ)^2$

$sin(A + B) = sinAcosB + cosAsinB$

$cos(A + B) = cosAcosB - sinAsinB$

$sin(A - B) = sinAcosB - cosAsinB$

$cos(A - B) = cosAcosB + sinAsinB$

$sin(2x) = 2sinxcosx$

$cos(2x) = 2(cosx)^2 - 1 = 1 - 2(sinx)^2$

正弦定理

在任意一个平面三角形中，各边和它所对角的正弦值的比相等且等于外接圆的直径

$a/sinA = b/sinB = c/sinC = 2R$

余弦定理

在任意一个平面三角形中，任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。

$a^2 = b^2 + c^2 -2bccosA$

$b^2 = a^2 + c^2 -2accosB$

$c^2 = a^2 + b^2 -2abcosC$

海伦公式

设三角形的三条边为abc.则面积s

$p = (a + b + c) / 2$

$s = \sqrt[2]{p(p-a)(p-b)(p-c)}$

三角函数的极限

小数的情况

${\lim_{x \to 0} \frac{sinx}{x}} = 1$

$\lim_{x \to 0} cosx = 1$

$\lim_{x \to 0} \frac{tanx}{x} = 1$

$\lim_{x \to 0} \frac{1-cosx}{x} = 0$

大数的情况

考虑极限 $\lim_{x \to \infty}$

对于任意的x $-1 <= sinx <=1$ $-1 <=cosx <= 1$

应用三明治定理 $\lim_{x \to \infty} \frac{sinx}{x} = 0$

其他情况

考虑极限 $\lim_{x \to \frac{\pi}{2}}\frac{cosx}{x-\frac{\pi}{2}}$ 这次的三角函数是余弦, 且要在 π/2 的附近求值. 这既不是小数的情况也不是大数的情况, 因此很明显, 之前的情况都不适用.面对 x → a 的极限, 而a != 0 时, 有一个很好的一般原则, 那就是用 t = x − a作替换, 将问题转化为 t→0

$\lim_{x \to \dfrac{\pi}{2}}\frac{cosx}{x-\frac{\pi}{2}}$

$\lim_{t \to 0}\frac{cos(t+\frac{\pi}{2})}{t}$

$cos(\frac{\pi}{2}+t) = sin(-t) = -sint$

$\lim_{t \to 0}\frac{-sint}{t} = -1$

三角函数的导数

$\frac{\mathrm{d}}{\mathrm{d}x}sinx = cosx$

$\frac{\mathrm{d}}{\mathrm{d}x}cosx = -sinx$

$\frac{\mathrm{d}}{\mathrm{d}x}tanx = (secx)^2$

$\frac{\mathrm{d}}{\mathrm{d}x}secx = secxtanx$

$\frac{\mathrm{d}}{\mathrm{d}x}cscx = -cscxcotx$

$\frac{\mathrm{d}}{\mathrm{d}x}cotx = -(cscx)^2$

参考

普林斯顿微积分读本