本文已参与「新人创作礼」活动，一起开启掘金创作之路。

图的应用——最小生成树（Prim算法和Kruskal）与最短路径（Dijkstra算法和Floyd算法）

1 最小生成树

构造连通网的最小代价生成树称为最小生成树（Mininum Cost Spanning Tree）。找连通网的最小生成树，经典的有两种算法，普里姆算法和克鲁斯卡尔算法。

1.1 普里姆(Prim)算法

我们先构造邻接矩阵，如图所示：

从 $v_0$ 开始， $v_0$ 旁有两条边, 10与11比, 10更小一些些。所以选 $v_0$ 至 $v_1$ 的边为最小生成树的第—条边，如左下图所示。然后我们看 $v_0$ 和 $v_1$ 两个顶点的其他边，有11、16、12、18，这里面最小的是11，所以 $v_0$ 到 $v_5$ 的边为最小生成树的第二条边，如中下图所示。然后我们看 $v_0$ 、 $v_1$ 和 $v_5$ 三个顶点的其他边，有18、12、16、17、26，这里面最小的是12，所以 $v_1$ 到 $v_8$ 的边为最小生成树的第三条边，如右下图所示。

类似的方法，我们可以得到下面的六张图：

Prim算法实现代码如下：

/* Prim算法生成最小生成树  */
void MiniSpanTree_Prim(MGraph G)
{
	int min, i, j, k;
	int adjvex[MAXVEX];		/* 保存相关顶点下标 */
	int lowcost[MAXVEX];	/* 保存相关顶点间边的权值 */
	lowcost[0] = 0;/* 初始化第一个权值为0，即v0加入生成树 */
			/* lowcost的值为0，在这里就是此下标的顶点已经加入生成树 */
	adjvex[0] = 0;			/* 初始化第一个顶点下标为0 */
	for(i = 1; i < G.numVertexes; i++)	/* 循环除下标为0外的全部顶点 */
	{
		lowcost[i] = G.arc[0][i];	/* 将v0顶点与之有边的权值存入数组 */
		adjvex[i] = 0;					/* 初始化都为v0的下标 */
	}
	for(i = 1; i < G.numVertexes; i++)
	{
		min = GRAPH_INFINITY;	/* 初始化最小权值为∞， */
						/* 通常设置为不可能的大数字如32767、65535等 */
		j = 1;k = 0;
		while(j < G.numVertexes)	/* 循环全部顶点 */
		{
			if(lowcost[j]!=0 && lowcost[j] < min)/* 如果权值不为0且权值小于min */
			{	
				min = lowcost[j];	/* 则让当前权值成为最小值 */
				k = j;			/* 将当前最小值的下标存入k */
			}
			j++;
		}
		printf("(%d, %d)\n", adjvex[k], k);/* 打印当前顶点边中权值最小的边 */
		lowcost[k] = 0;/* 将当前顶点的权值设置为0,表示此顶点已经完成任务 */
		for(j = 1; j < G.numVertexes; j++)	/* 循环所有顶点 */
		{
			if(lowcost[j]!=0 && G.arc[k][j] < lowcost[j]) 
			{/* 如果下标为k顶点各边权值小于此前这些顶点未被加入生成树权值 */
				lowcost[j] = G.arc[k][j];/* 将较小的权值存入lowcost相应位置 */
				adjvex[j] = k;				/* 将下标为k的顶点存入adjvex */
			}
		}
	}
}

1.2 克鲁斯卡尔(Kruskal)算法

普里姆算法是以某顶点为起点，逐步找各顶点上最小权值的边来构建最小生成树。同样的思路’我们也可以直接就以边为目标去构建，因为权值是在边上，直接去找最小权值的边来构建生成，只不过构建时要考虑是否会形成环路而已。

我们将同样的图的邻接矩阵通过程序转化为右下图的边集数组，并旦对它们按权值从小到大排序。

克鲁斯卡尔算法的思想就是站在了上帝视角，先把权值最短的边—个个挑出来。左图找到了权值最短边 $v_7$ 和 $v_4$ ，中下图找到了权值第二短边 $v_2$ 和 $v_8$ ，右下图找到了权值第三短边 $v_0$ 和 $v_1$ 。

我们找到了大量的权值短边后’发现了—个问题。比如当完成到左下图的情况时，我们接下来去找权值最小的边应该是 $v_6$ 和 $v_5$ ，这条边的权值是17，但是这会带来一个结果, $v_6$ 和 $v_5$ 已经通过中转的顶点 $v_0$ 和 $v_1$ 连通了，它们并不需要继续再关联否则就是重复。而 $v_6$ 和 $v_5$ 两个顶点更应该与顶点 $v_3$ 、 $v_7$ 和 $v_4$ 进行连接。检查了它们的权值，22、21、24、19、26，最终选择了19作为最小的权值边。如右下图，完成最小生成树的构建。

克鲁斯卡尔算法实现代码如下：

/* 查找连线顶点的尾部下标 */
int Find(int *parent, int f)
{
	while ( parent[f] > 0)
	{
		f = parent[f];
	}
	return f;
}

/* 生成最小生成树 */
void MiniSpanTree_Kruskal(MGraph G)
{
	int i, j, n, m;
	int k = 0;
	int parent[MAXVEX];/* 定义一数组用来判断边与边是否形成环路 */
	
	Edge edges[MAXEDGE];/* 定义边集数组,edge的结构为begin,end,weight,均为整型 */

	/* 用来构建边集数组并排序********************* */
	for ( i = 0; i < G.numVertexes-1; i++)
	{
		for (j = i + 1; j < G.numVertexes; j++)
		{
			if (G.arc[i][j]<GRAPH_INFINITY)
			{
				edges[k].begin = i;
				edges[k].end = j;
				edges[k].weight = G.arc[i][j];
				k++;
			}
		}
	}
	sort(edges, &G);
	/* ******************************************* */


	for (i = 0; i < G.numVertexes; i++)
		parent[i] = 0;	/* 初始化数组值为0 */

	printf("打印最小生成树：\n");
	for (i = 0; i < G.numEdges; i++)	/* 循环每一条边 */
	{
		n = Find(parent,edges[i].begin);
		m = Find(parent,edges[i].end);
		if (n != m) /* 假如n与m不等，说明此边没有与现有的生成树形成环路 */
		{
			parent[n] = m;	/* 将此边的结尾顶点放入下标为起点的parent中。 */
							/* 表示此顶点已经在生成树集合中 */
			printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight);
		}
	}
}

2 最短路径

2.1 迪杰斯特拉(Dijkstra)算法

迪杰斯特拉算法不是一下子求出 $v_0$ 到 $v_8$ 的最短路径，而是一步步求出它们之间顶点的最短路径，过程中都是基于已经求出的最短路径的基础上，求得更远顶点的最短路径。

迪杰斯特拉（Dijkstra）的数据结构：

#define MAXEDGE 20
#define MAXVEX 20
#define GRAPH_INFINITY 65535

typedef struct
{
	int vexs[MAXVEX];
	int arc[MAXVEX][MAXVEX];
	int numVertexes, numEdges;
}MGraph;

typedef int Patharc[MAXVEX];    /* 用于存储最短路径下标的数组 */
typedef int ShortPathTable[MAXVEX];/* 用于存储到各点最短路径的权值和 */

算法代码如下：

/*  Dijkstra算法，求有向网G的v0顶点到其余顶点v的最短路径P[v]及带权长度D[v] */    
/*  P[v]的值为前驱顶点下标,D[v]表示v0到v的最短路径长度和 */  
void ShortestPath_Dijkstra(MGraph G, int v0, Patharc *P, ShortPathTable *D)
{    
	int v,w,k,min;    
	int final[MAXVEX];/* final[w]=1表示求得顶点v0至vw的最短路径 */
	for(v=0; v<G.numVertexes; v++)    /* 初始化数据 */
	{        
		final[v] = 0;			/* 全部顶点初始化为未知最短路径状态 */
		(*D)[v] = G.arc[v0][v];/* 将与v0点有连线的顶点加上权值 */
		(*P)[v] = -1;				/* 初始化路径数组P为-1  */       
	}

	(*D)[v0] = 0;  /* v0至v0路径为0 */  
	final[v0] = 1;    /* v0至v0不需要求路径 */        
	/* 开始主循环，每次求得v0到某个v顶点的最短路径 */   
	for(v=1; v<G.numVertexes; v++)   
	{
		min=GRAPH_INFINITY;    /* 当前所知离v0顶点的最近距离 */        
		for(w=0; w<G.numVertexes; w++) /* 寻找离v0最近的顶点 */    
		{            
			if(!final[w] && (*D)[w]<min)             
			{                   
				k=w;                    
				min = (*D)[w];    /* w顶点离v0顶点更近 */            
			}        
		}        
		final[k] = 1;    /* 将目前找到的最近的顶点置为1 */
		for(w=0; w<G.numVertexes; w++) /* 修正当前最短路径及距离 */
		{
			/* 如果经过v顶点的路径比现在这条路径的长度短的话 */
			if(!final[w] && (min+G.arc[k][w]<(*D)[w]))   
			{ /*  说明找到了更短的路径，修改D[w]和P[w] */
				(*D)[w] = min + G.arc[k][w];  /* 修改当前路径长度 */               
				(*P)[w]=k;        
			}       
		}   
	}
}

在执行算法之前，先准备邻接矩阵 MGraph的G，如右下图所示，并且定义参数 $v_0$ 为0

算法执行流程：

第六行final数组是为了 $v_0$ 到某顶点是否已经求得最短路径的标记，如果 $v_0$ 到 $v_w$ 已经有结果，则final[w]=1。
第 $7-12$ 行，是在对数据进行初始化。此时final数组值均为0，表示所有的点都未求得最短路径。D数组为 $\{65535,1,65535,65535,65535,65535,65535,65535\}$ 。因为 $v_0$ 与 $v_1$ 和 $v_2$ 的边权值为1和5。P数组全为-1，表示目前没有路径。
第13行，表示 $v_0$ 到 $v_0$ 自身，权值和结果为0，D数组为 $\{0,1,5,65535,65535,65535,65535,65535\}$ 。第14行，表示 $v_0$ 点算是已经求得的最短路径，因此final[0]=1。此时final数组为{1,0,0,0,0,0,0,0}。此时初始化工作完成。
第16-37行，为主循环，每次循环求得 $v_0$ 与一个顶点的最短路径。因为 $v$ 从1而不是0开始。
第18-26行。先令min为65535的极大值，通过w循环，与D[w]比较找到最小值min=1，k=1。
第27行，由k=1，表示与 $v_0$ 最近的顶点是 $v_1$ ，并且由D[1]=1，知道此时 $v_0$ 到 $v_1$ 的最短距离是1。因此将 $v_1$ 对应的final[1]设置为1.此时final数组为{1,1,0,0,0,0,0,0}。
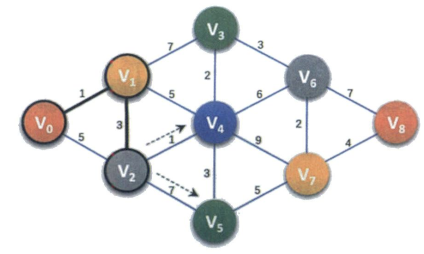
第28-36行是一循环，它的目的是在刚才已经找到 $v_0$ 与 $v_1$ 的最短路径的基础上，对 $v_1$ 与其他顶点的边进行计算，到 $v_0$ 与他们的当前最短距离，如图所示。因为min=1，所以本来D[2]=5，现在 $v_0\rarr v_1 \rarr v_2=D[2]=min+3=4$ ， $v_0 \rarr v_1 \rarr v_3=D[3]=min+7=8$ ， $v_0\rarr v_1 \rarr v_4=D[4]=min+5=6$ ，因此，D数组当前值为{0,1,4,8,6,65535,65535,65535,65535}。而p[2]=1,P[3]=1,P[4]=1，它表示的意思是 $v_0$ 到 $v_2$ 、 $v_3$ 、 $v_4$ 点的最短路径他们的前驱均是-1，此时P数组值为{-1，-1，1，1，1，-1，-1，-1，-1}。
重新开始循环,此时v＝2。第18-26行，对W循环，注意区为final[0]=1和final[1]＝1,由第21行的!final[w]可知， $v_0$ 与 $v_1$ 并不参与最小值的获取。通过循环比较，找到最小值min=4，k＝2。
第27行，由k＝2，表示已经求出 $v_0$ 到 $v_2$ 的最短路径，并且由D[2]=4，知道最短距离是4。因此将 $v_2$ 对应的final[2]设置为1，此时final数组为{1,1,1,0,0,0,0,0,0}。
第28-36行，在刚才已经找到 $v_0$ 与 $v_2$ 的最短路径的基础上，对 $v_2$ 与其他顶点的边进行计算，得到 $v_0$ 与它们的当前最短距离，如下图所示。区为min=4，所以本来D[4]＝6，现在 $v_0\rarr v_2 \rarr v_4=D[4]=min+1=5$ ， $v_0\rarr v_2 \rarr v_5=D[5]=min+7=11$ 。因此，D数组当前值为{0,1,4,8,5,11,65535,65535,65535}。而原本P[4]=1，此时P[4]=2， P[5]=2，它表示 $v_0$ 到 $v_4$ 、 $v_5$ 点的最短路径它们的前驱均是 $v_2$ 。此时P数组值为{-1，-1，1，1，2，2，-1，-1，-1}。

![image-20220911205138063.png](https://s2.loli.net/2022/09/11/2g973wSphd5jRMN.png)

重新开始循环，此时v=3。第17-25行，通过对w循环比较找到最小值min=5，k=4。
第27行，由k=4，表示已经 $v_0$ 到 $v_4$ 的最短路径，并且由D[4]=5，知道最短距离是5。因此将 $v_4$ 对应的final[4]设置为1。此时final数组为{1,1,1,0,1,0,0,0,0,0}。
第28-36行，对 $v_4$ 与其他顶点的边进行计算，得到 $v_0$ 与他们的当前最短距离，如下图所示。因为min=5，所以D[3]=8，现在 $v_0\rarr v_4 \rarr v_3=D[3]=min+2=7$ ，本来D[5]=11，现在 $v_0\rarr v_4 \rarr v_7=D[7]=min+9=14$ ，因此，D数组当前值为{0,1,4,7,5,8,11,14,65535}。而原本P[3]=1，此时P[3]=4，它表示 $v_0$ 到 $v_3$ 、 $v_5$ 、 $v_6$ 、 $v_7$ 点的最短路径它们的前驱是 $v_4$ ，此时P数组值为{-1，-1，1，4，2，4，4，-1}。
之后的循环就完全类似了。得到最终的结果，如下图所示。此时final数组为{1,1,1,1,1,1,1,1}，它表示所有的顶点均完成了最短路径的查找工作。此时D数组为｛0，1，4，7，5，8，10，12，16}，它表示到各个顶点的最短路径数，比如 $D[8]=1+3+1+2+3+2+4=16$ 。此时P数组值为{-1,-1,1,4,2,4,3,6,7}，这串数字可能略为难理解。比如P[8]=7，它的意思是 $v_0$ 到 $v_8$ 的最短路径，顶点 $v_0$ 的前驱顶点是 $v_7$ ，再由P[7]=6，表示 $v_7$ 的前驱是 $v_6$ ，P[6]=3，表示 $v_6$ 的前驱是 $v_3$ 。这样就可以得到， $v_0$ 到 $v_8$ 的最短路径为 $v_8\larr v_7 \larr v_6 \larr v_3 \larr v_4 \larr v_2 \larr v_1 \larr v_0$ ，即 $v_0\rarr v_1 \rarr v_2 \rarr v_4 \rarr v_3 \rarr v_6 \rarr v_7 \rarr v_8$ 。

2.2 弗洛伊德(Floyd)算法

弗洛伊德算法是基于动态规划算法实现的，接下来以在下图所示的有向加权图中查找各个顶点之间的最短路径为例。

弗洛伊德算法查找上图中各个顶点之间的最短路径，实现过程如下：

建立一张表格，记录每个顶点直达其它所有顶点的权值。

起始顶点指的是从哪个顶点出发，目标顶点指的是要达到的顶点，例如 2->1 路径的权值是 2，顶点 2 是起始顶点，顶点 1 是目标顶点。此外，∞ 表示无穷大的数，即顶点之间不存在直达的路径。
在表 1 的基础上，将顶点 1 作为 "中间顶点"，计算从各个顶点出发途径顶点 1 再到达其它顶点的权值，如果比表 1 中记录的权值更小，证明两个顶点之间存在更短的路径，对表 1 进行更新。

从各个顶点出发，途径顶点 1 再到达其它顶点的路径以及对应的权值分别是：
- 2-1-3：权值为 2 + ∞ = ∞，表 1 中记录的 2-3 的权值也是 ∞；
- 2-1-4：权值为 2 + 5 = 7，表 1 中记录的 2-4 的权值是 4；
- 3-1-2：权值为 ∞ + 3，表 1 中记录的 3-2 的权值是 1；
- 3-1-4：权值为 ∞ + 5，表 1 中记录的 3-4 的权值是 ∞；
- 4-1-2：权值为 ∞ + 3，表 1 中记录的 4-2 的权值是 ∞；
- 4-1-3：权值为 ∞ + ∞，表 1 中记录的 4-3 的权值是 2。
以上所有的路径中，没有比表 1 中记录的权值最小的路径，所以不需要对表 1 进行更新。
在表 1 的基础上，以顶点 2 作为 "中间顶点"，计算从各个顶点出发途径顶点 2 再到达其它顶点的权值：

1-2-3：权值为 3 + ∞，表 1 中记录的 1-3 的权值为 ∞；
1-2-4：权值为 3 + 4 = 7，表 1 中 1-4 的权值为 5；
3-2-1：权值为 1 + 2 = 3，表 1 中 3-1 的权值为 ∞，3 < ∞；
3-2-4：权值为 1 + 4 = 5，表 1 中 3-4 的权值为 ∞，5 < ∞；
4-2-1：权值为 ∞ + 2，表 1 中 4-1 的权值为 ∞；
4-2-3：权值为 ∞ + ∞，表 1 中 4-3 的权值为 2。

以顶点 2 作为 "中间顶点"，我们找到了比 3-1、3-4 更短的路径，对表 1 进行更新：

在表 2 的基础上，将顶点 3 作为 "中间顶点"，计算从各个顶点出发途径顶点 3 再到达其它顶点的权值：
- 1-3-2 权值为 ∞ + 1，表 2 中 1-2 的权值为 3；
- 1-3-4 权值为 ∞ + 5，表 2 中 1-4 的权值为 5；
- 2-3-1 权值为 ∞ + 3，表 2 中 2-1 的权值为 2；
- 2-3-4 权值为 ∞ + 5，表 2 中 2-4 的权值为 4；
- 4-3-1 权值为 2 + 3 = 5，表 2 中 4-1 的权值为 ∞，5 < ∞；
- 4-3-2 权值为 2 + 1 = 3，表 2 中 4-2 的权值为 ∞，3 < ∞；
以顶点 3 作为 "中间顶点"，我们找到了比 4-1、4-2 更短的路径，对表 2 进行更新：
在表 3 的基础上，将顶点 4 作为 "中间顶点"，计算从各个顶点出发途径顶点 4 再到达其它顶点的权值：
- 1-4-2 权值为 5 + 3 = 8，表 3 中 1-2 的权值为 3；
- 1-4-3 权值为 5 + 2 = 7，表 3 中 1-3 的权值为 ∞，7 < ∞；
- 2-4-1 权值为 4 + 5 = 9，表 3 中 2-1 的权值为 2；
- 2-4-3 权值为 4 + 2 = 6，表 3 中 2-3 的权值为 ∞，6 < ∞；
- 3-4-1 权值为 4 + 5 = 9，表 3 中 3-1 的权值为 3；
- 3-4-2 权值为 5 + 5 = 10 ，表 3 中 3-2 的权值为 1。
以顶点 4 作为 "中间顶点"，我们找到了比 1-3、2-3 更短的路径，对表 3 进行更新：

通过将所有的顶点分别作为“中间顶点”，最终得到的表 4 就记录了各个顶点之间的最短路径。例如，4-1 的最短路径为 4-3-2-1。

Floyd算法实现：

#define V 4    //设定图中的顶点数
#define INF 65535   // 设置一个最大值
int P[V][V] = { 0 }; //记录各个顶点之间的最短路径
void printMatrix(int matrix[][V]);  //输出各个顶点之间的最短路径
void printPath(int i, int j); // 递归输出各个顶点之间最短路径的具体线路
void floydWarshall(int graph[][V]); // 实现弗洛伊德算法
int main() {
    // 有向加权图中各个顶点之间的路径信息
    int graph[V][V] = { {0, 3, INF, 5},
                          {2, 0, INF, 4},
                          {INF, 1, 0, INF},
                          {INF, INF, 2, 0} };
    floydWarshall(graph);
}
// 中序递归输出各个顶点之间最短路径的具体线路
void printPath(int i, int j)
{
    int k = P[i][j];
    if (k == 0)
        return;
    printPath(i, k);
    printf("%d-", k + 1);
    printPath(k, j);
}
// 输出各个顶点之间的最短路径
void printMatrix(int graph[][V]) {
    int i, j;
    for (i = 0; i < V; i++) {
        for (j = 0; j < V; j++) {
            if (j == i) {
                continue;
            }
            printf("%d - %d: 最短路径为:", i + 1, j + 1);
            if (graph[i][j] == INF)
                printf("%s\n", "INF");
            else {
                printf("%d", graph[i][j]);
                printf("，依次经过：%d-", i + 1);
                //调用递归函数
                printPath(i, j);
                printf("%d\n", j + 1);
            }
        }
    }
}
// 实现弗洛伊德算法,graph[][V] 为有向加权图
void floydWarshall(int graph[][V]) {
    int  i, j, k;
    //遍历每个顶点，将其作为其它顶点之间的中间顶点，更新 graph 数组
    for (k = 0; k < V; k++) {
        for (i = 0; i < V; i++) {
            for (j = 0; j < V; j++) {
                //如果新的路径比之前记录的更短，则更新 graph 数组
                if (graph[i][k] + graph[k][j] < graph[i][j]) {
                    graph[i][j] = graph[i][k] + graph[k][j];
                    //记录此路径
                    P[i][j] = k;
                }
            }
        }
    }
    // 输出各个顶点之间的最短路径
    printMatrix(graph);
}