本文已参与[新人创作礼]活动,一起开启掘金创作之路
转载请注明出处.
图形学的数学基础(二十六):step和smoothStep
阶梯函数step
step函数接受两个参数,一个边界值edge,一个输入变量x,当x>=edge时,返回1, 否则返回0。

函数图像如下:
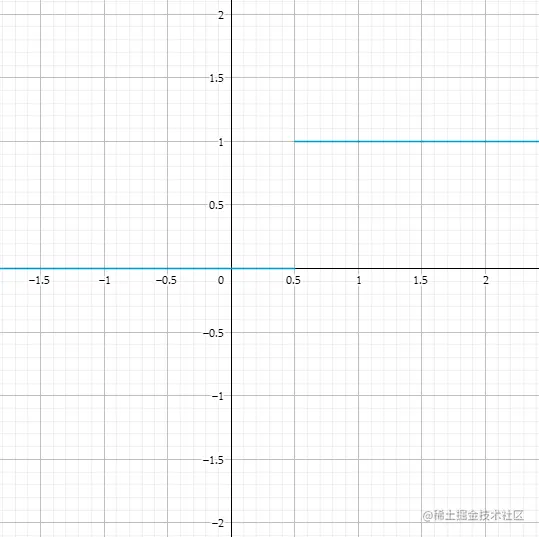
平滑阶梯函数(SmoothStep)
定义
smoothStep函数用来生成0到1的平滑过渡值.先看smoothStep函数实现:

数学推导
通过smoothStep函数定义,我们知道:
- res=3t2−2t3
- t=(b−a)(x−a)
接下来我们一步步通过函数图像来解释smoothStep背后的数学原理.
<1> 对于函数y=x这个函数,其实就是一条直线:
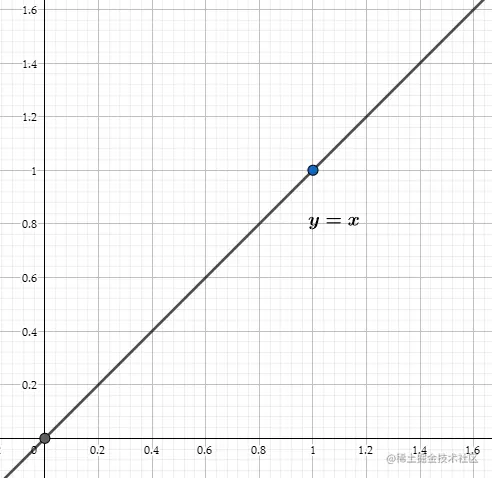
<2>对于函数y=x2,可以看到它比y=x有一个更平滑的过渡:
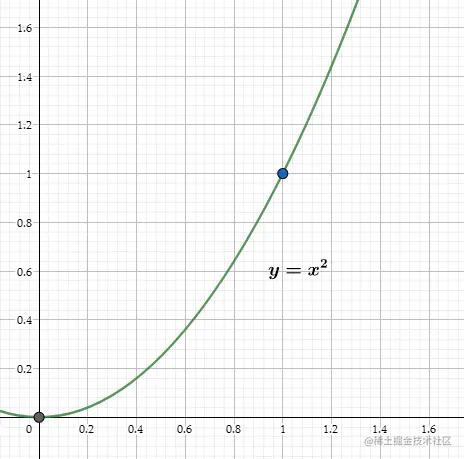
但是我们发现y=x2的函数图像仍然是不够“平滑的”,为什么呢?我们知道曲线的切线表示了这条曲线的变化率。通过观察我们明显发现,在0附近的变化率要低于1附近的变化率。
<3> y=1−(x−1)2我们在y=x2的基础上构造另外一条曲线.首先先将下2反转.得到:
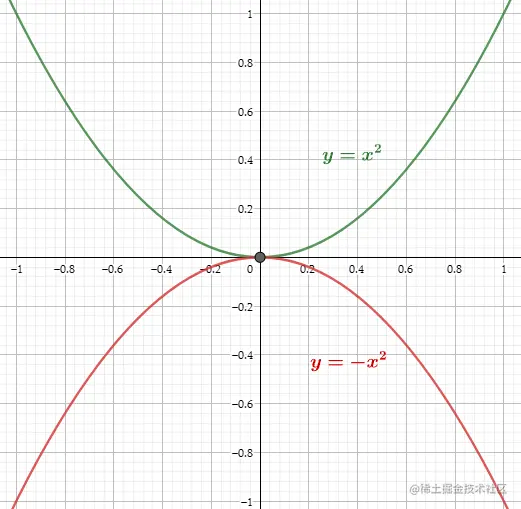
将y=−x2向右移动一个单位得到:
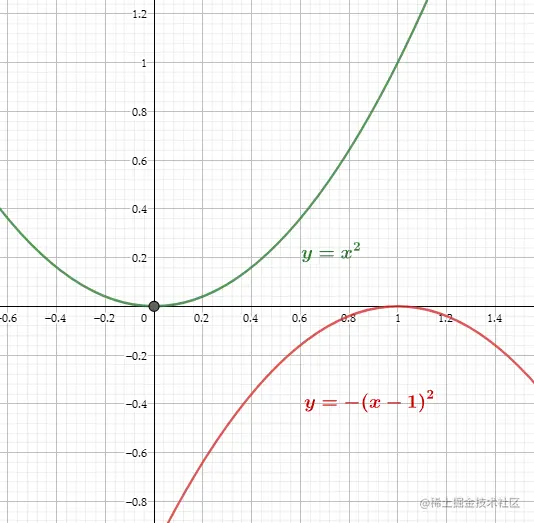
然后再向上移动一个单位得到以下函数图像:
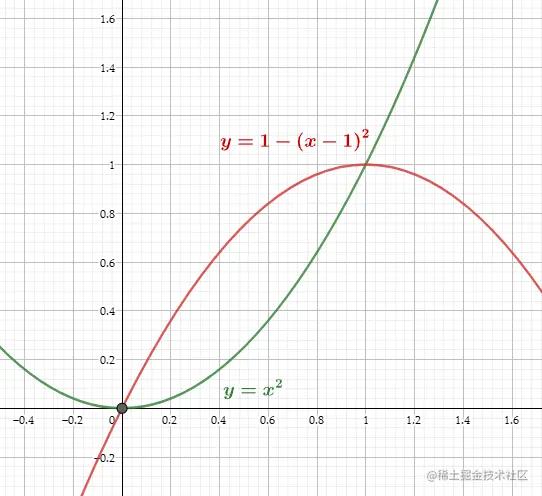
此时y=1−(x−1)2
可以看到我们构造的第二条曲线在接近1的部分开始变缓,和y=x2从0开始变缓一样.因此我们将这两条曲线混合到一起即可以得到理想情况下的“平滑过渡”:
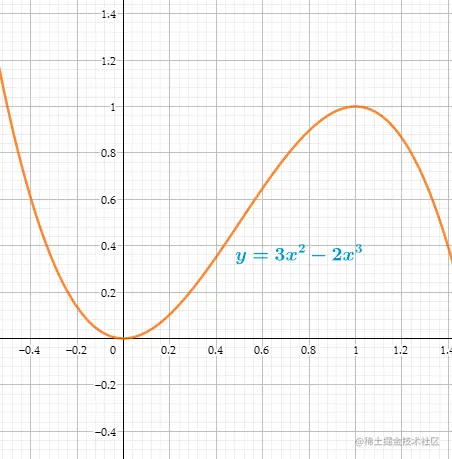
利用线性插值混合两条曲线:
y=xf(x)+(1−x)g(x)=x(1−(x−1)2)+(1−x)x2=3x2−2x3
参考
Scratchapixel
GAMES101 -现代计算机图形学入门-闫令琪
SmoothStep函数/节点到底做了什么?