图形学的数学基础（二十二）： $AABB$ 与光线求交

包围盒常用来做物体的碰撞监测，光线的相交测试等。尤其在光线追踪中，包围盒常用来做光线与物体相交测试。基本思想是这样的，我们将包围盒的长方体看做是三对互相平行的平面相交所形成的区域。尤其对于 $AABB$ ，每一对平行面都是与一个轴对齐的。根据这个特性，先以二维空间举例：

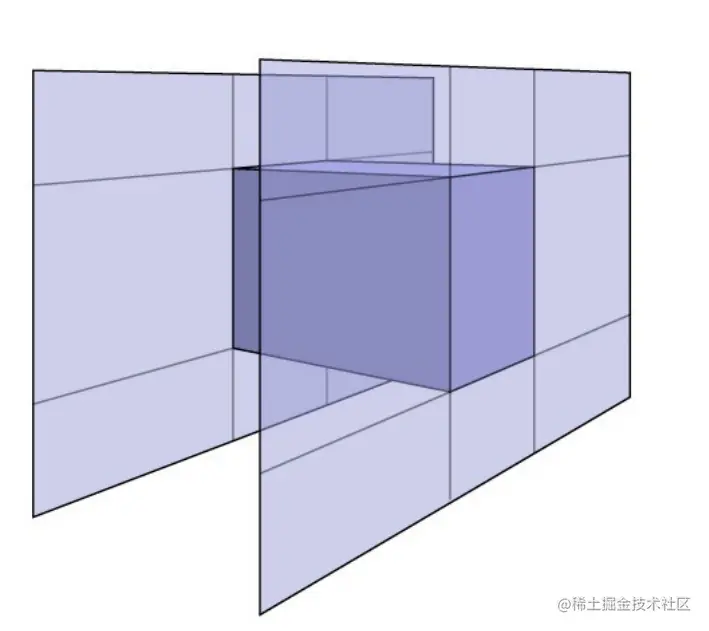
$AABB$ 由两对平面构成，分别是平行于 $x轴和y轴$ 。根据光线公式可知：

$Ray = \textbf{0} + \textbf{d}t$

其中o为光线起点，d为光线方向，Ray是光线经过t时间到达的位置。

如何判定光线是否与包围盒相交呢？我们可以通过分解，将问题简化，将光线分别穿过每对无线延申的平面，分别求出其 $T_{min}和T_{max}$ ：

与 $x$ 轴垂直的一对平面的交点：

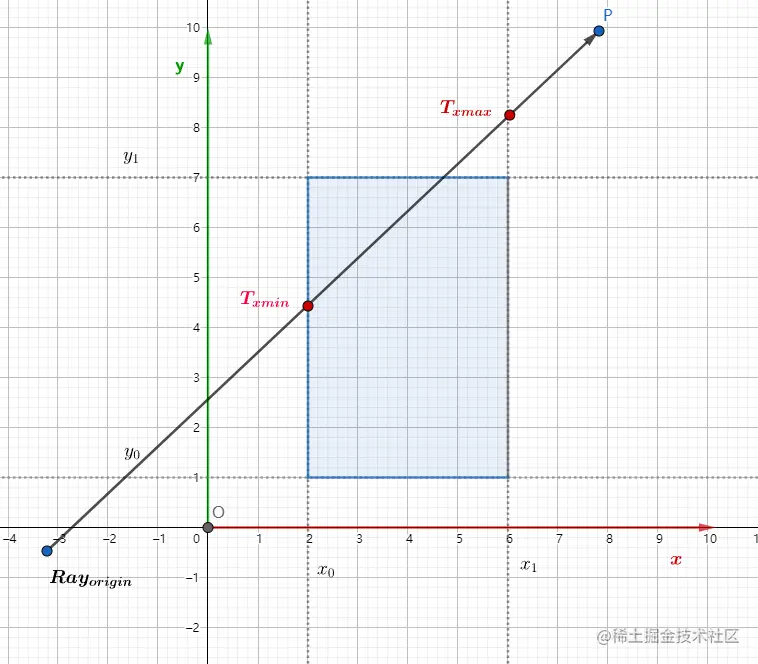
$T_{xmin}d_x + o_x = x_0$

$T_{xmin} = \dfrac{x_0 - o_x}{d_x}$

$T_{xmax}d_x + o_x = x_1$

$t_{xmax} = \dfrac{x_1 - o_x}{d_x}$

与 $y$ 轴垂直的一对平面的交点：

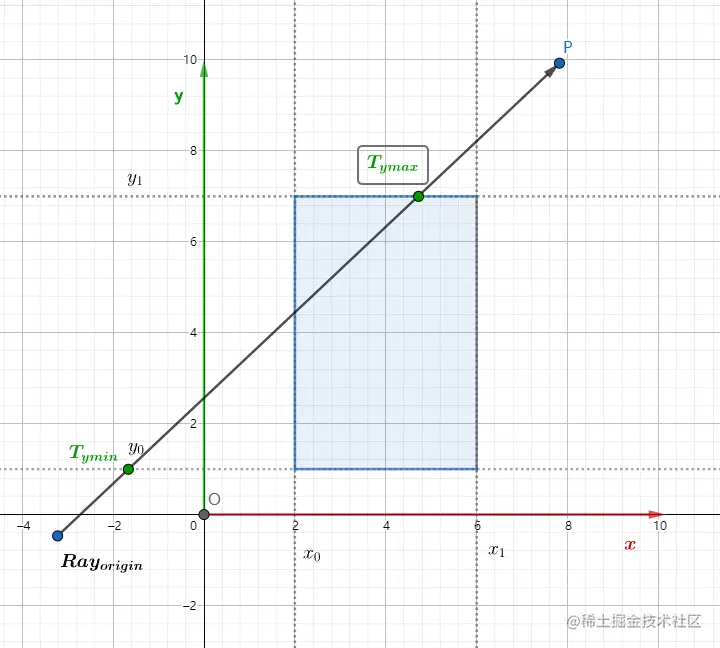
$T_{ymin}d_y + o_y = y_0$

$T_{ymin} = \dfrac{y_0 - o_y}{d_y}$

$T_{ymax}d_y + o_y = y_1$

$t_{ymax} = \dfrac{y_1 - o_y}{d_y}$

现在我们想象空间中的一条光线，只有当光线进入了所有的“平面对”，才算进入了盒子，光线只要离开了任何“平面对”，就算离开了盒子，因此光线进入盒子的时间实际上是进入所有“平面对”的最大值，即最小时间的最大值，而离开盒子的时间是光线离开“平面对”的最小值，即最大时间的最小值。（求交）

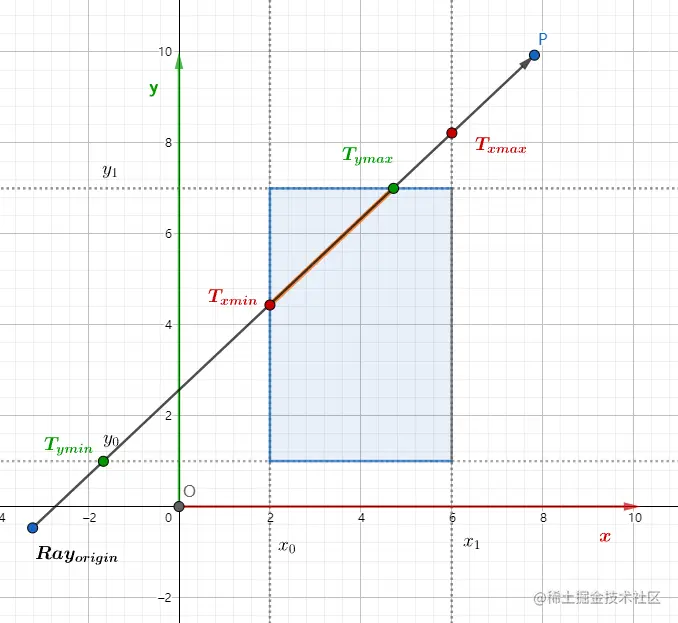
考虑三维情况下光线与 $AABB$ 求交。关键点：

对于三维空间，我们有三组“平面对”，分别计算 $t_{min}和t_{max}$ ，因此有：

$t_{enter} = max(t_{minx}, t_{miny}, t_{minz})$

$t_{exit} = min(t_{maxx}, t_{maxy}, t_{maxz})$

当且仅当 $t_{enter} < t_{exit}$ 时，我们认为“光线在盒子里停留了一段时间”，即光线与盒子相交。

但是以上推断没有考虑t为负值的情况，当 $t_{exit} < 0$ 时，盒子在光线背面，必然不会出现交点（光线是单向的），当 $t_{exit} >= 0 并且t_{enter} < 0时$ ，光线起点在盒子里边，那么光线必然与盒子相交。因此得出结论：

光线 $Ray$ 与 $AABB$ 相交，当且仅当：

$t_{enter} < t_{exit}$
$t_{exit} \;\;>= 0$

参考