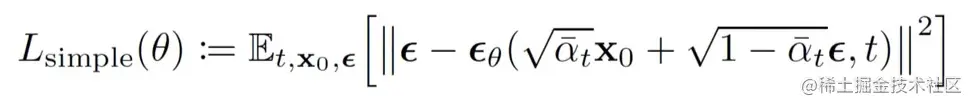diffusion Model原理之扩散过程与逆扩散过程

机器学习炼丹术
2,400 阅读2分钟

前面推导了一些铺垫知识，现在正式来看diffusion Model。

3 diffusion models

image.png

我们说的扩散过程，就是从x0x_0到xTx_T的过程，也就是墒增的过程，从有序到无序。反过来是叫做逆扩散过程。

所以可以看到，q模型是一个加噪音的模型，p模型是一个去噪音的过程。

3.1 扩散过程

  • 给定初始数据分布x0∼q(x)x_0 \sim q(x),可以不断向分布中添加高斯噪音，该噪音的标准差是以固定值βt\beta_t而确定的，而均值是以固定值βt\beta_t和当前t时刻的xtx_t决定的。这个过程是一个马尔可夫链过程。
  • 随着t不断增大，最终数据分布xTx_T变成了一个各向独立的高斯分布。

q(xt∣xt−1)=N(xt;1−βtxt−1,βtI)q(x_t|x_{t-1})=N(x_t;\sqrt{1-\beta_t}x_{t-1},\beta_tI)

q(x1:T∣x0)=∏t=1Tq(xt∣xt−1)q(x_{1:T}|x_0) = \prod_{t=1}^T q(x_t|x_{t-1})

  • 这里会用到参数重整化的技巧，我们知道xtx_t服从这个正态分布，所以我们从标准正态分布中采样出z，然后与1−βtxt−1\sqrt{1-\beta_t}x_{t-1}均值相加，与βt\beta_t标准差相乘。

这里βt>βt−1\beta_{t}>\beta_{t-1}

这里推导一下，我们的xtx_t可以表示为xt−1x_{t-1}的函数，也可以表示为x0x_0的函数。我们这里设定αt=1−βt\alpha_t=1-\beta_t

xt=αtxt−1+1−αt∗zx_t=\sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_t}*z

上面公式中z为正态高斯分布，且利用了参数重整化的技巧。（reparameterization trick）

xt=αt(αt−1xt−2+1−αt−1∗z)+1−αt∗zx_t=\sqrt{\alpha_t}(\sqrt{\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_{t-1}}*z)+\sqrt{1-\alpha_t}*z

=αtαt−1xt−2+αt(1−αt−1)z+1−αtz=\sqrt{\alpha_t\alpha_{t-1}}x_{t-2}+\sqrt{\alpha_t(1-\alpha_{t-1})}z+\sqrt{1-\alpha_t}z

两个高斯分布相加a+b，那么新分布的方差是a2+b2a^2+b^2.所以上面公式可以化简成：

=αtαt−1xt−2+1−αtαt−1z=\sqrt{\alpha_t\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_t\alpha_{t-1}}z

所以我们继续递归上面公式，可以得到： xt=∏i=1tαix0+1−∏i=1tαizx_t = \sqrt{\prod_{i=1}^t{\alpha_i}} x_0+ \sqrt{1-\prod_{i=1}^t{\alpha_i}}z

设置αtˉ=∏i=1tαi\bar{\alpha_t}=\prod_{i=1}^t{\alpha_i}

则q(xt∣x0)=N(xt;αtˉx0,(1−αtˉ)I)q(x_t|x_0)=N(x_t;\sqrt{\bar{\alpha_t}}x_0,(1-\bar{\alpha_t})I)

所以我们大概可以计算出来，当t需要多大的时候，αtˉ\bar{\alpha_t}是接近0的，就是独立同分布。

这里就可以看出来扩散模型和VAE的区别，从x到z的过程，vae是一个网络预测出来的z，而且并不能保证z和x是无关的；而扩散模型的扩散过程是一个无参的过程，并且z是一个各项同分布的一个分布，与x完全不相关。此外扩散模型的z和x是同尺寸的，而vae没有这个需求

当样本有着越来越多噪音的时候，可以采用更大的update step：

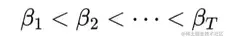
image.png

3.2 逆扩散过程

  • 逆过程是从高斯噪音中恢复原始数据。

pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))p_\theta(x_{t-1} | x_t)=N(x_{t-1};\mu_\theta(x_t,t),\Sigma_\theta(x_t,t))

现在我们需要推导一下后验扩散条件概率q(xt−1∣xt,x0)q(x_{t-1}|x_t,x_0)。

q(xt−1∣xt,x0)=q(xt−1,xt,x0)q(xt,x0)q(x_{t-1}|x_t,x_0)=\frac{q(x_{t-1},x_t,x_0)}{q(x_t,x_0)}

=q(xt∣xt−1,x0)q(xt−1∣x0)q(x0)q(xt∣x0)q(x0)=q(xt∣xt−1,x0)q(xt−1∣x0)q(xt∣x0)=\frac{q(x_t|x_{t-1},x_0)q(x_{t-1}|x_0)q(x_0)}{q(x_t|x_0)q(x_0)}=q(x_t|x_{t-1},x_0)\frac{q(x_{t-1}|x_0)}{q(x_t|x_0)}

因为这是马尔可夫过程，所以q(xt∣xt−1,x0)=q(xt∣xt−1)q(x_t|x_{t-1},x_0)=q(x_t|x_{t-1})

现在我们要重点考虑这个部分：

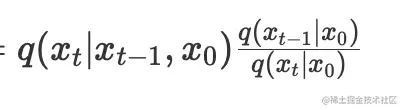
image.png

前者是：

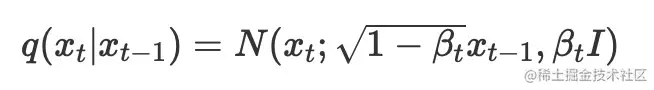
image.png

后者是：

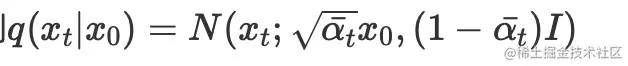
image.png

我们只考虑指数部分，因为系数部分一定是正数，所以成正比关系。

q(xt∣xt−1,x0)q(xt−1∣x0)q(xt∣x0)q(x_t|x_{t-1},x_0)\frac{q(x_{t-1}|x_0)}{q(x_t|x_0)}

∝exp(−12((xt−αtxt−1)2βt+(xt−1−αˉt−1x0)21−αˉt−1−(xt−αˉtx0)21−αˉt))\propto exp(-\frac{1}{2}( \frac{(x_t-\sqrt{\alpha_t}x_{t-1})^2}{\beta_t}+ \frac{(x_{t-1}-\sqrt{\bar{\alpha}_{t-1}}x_0)^2}{1-\bar{\alpha}_{t-1}}-\frac{(x_t-\sqrt{\bar{\alpha}_t}x_0)^2}{1-\bar{\alpha}_t} ))

我们要求解xt−1x_{t-1}，所以将上面公式整理一下形式：

exp(−12((αtβt+11−αˉt−1)xt−12+(−2αtxtβt+−2αˉt−1x01−αˉt−1)xt−1+C(xt,x0))exp(-\frac{1}{2}( (\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}})x_{t-1}^2 + (\frac{-2\sqrt{\alpha_t}x_t }{\beta_t}+\frac{-2\sqrt{\bar{\alpha}_{t-1}}x_0}{1-\bar{\alpha}_{t-1}})x_{t-1} + C(x_t,x_0))

后面顶不住了。。先歇着吧

image.png

avatar
文章
阅读
粉丝