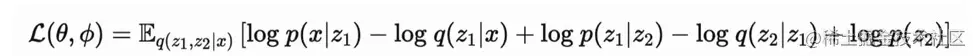另辟蹊径的生成算法！DDPM的铺垫知识

0 概述

我本来应该在学习Stable Diffusion的代码。但是因为其很大程度是依赖于DDPM的研究，所以现在沿着这棵树往上爬，必须要先干掉DDPM。

DDPM其中包含了很多的背景知识，比方说扩散模型和score matching。DDPM主要是提出了扩散模型通过一些参数化的手段，使其在形式上与score-based generative modeling的等效性。

这里基于一篇论文：

• 2015:Deep Unsupervised Learning using Nonequilibrium Thermodynamics

生成模型有5类：

• sequence2sequence
• GAN对抗生成
• flow-based generative model
• VAE生成模型
• Diffusion model

0 前置条件

0.1 条件概率公式

$P(A,B,C) = P(C|B,A)P(B,A)=P(C|B,A)P(B|A)P(A)$

$P(B,C|A) = P(C|A,B)P(B|A)$

那么如果满足马尔可夫假设的条件概率是什么样子的呢？ 马尔可夫假设：当前状态仅仅与上一时刻的状态有关，与更早的状态无关 如果满足马尔可夫链关系A->B->C,那么： $P(A,B,C)=P(C|B)P(B|A)P(A)$

同理

$P(B,C|A) = P(C|B)P(B|A)$

0.2 高斯分布和KL散度

单变量高斯分布的公式： $f(x)=\frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

KL散度公式： $KL[p||q]=E_{x\sim p}[log(\frac{p}{q})]$

所以两个单变量的高斯分布的KL散度可以写作：

$KL[p(x)||q(x)]=\int_x{\frac{1}{\sigma_1\sqrt{2\pi}}e^{\frac{-(x-\mu_1)^2}{2\sigma_1^2}}(log{\frac{\sigma_2}{\sigma_1}+\frac{(x-\mu_2)^2}{2\sigma_2^2}- \frac{(x-\mu_1)^2}{2\sigma_1^2} })}dx$

这个公式的第一个是常数项:

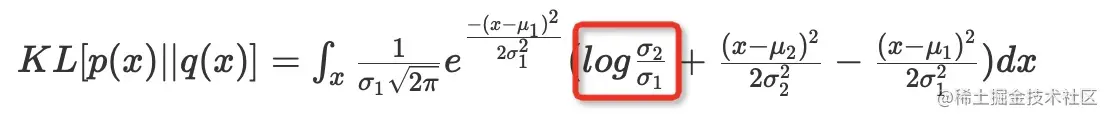
这个公式的第三项等于$\frac{1}{2}$（因为高斯分布的方差定义）。

第二项其中关键在于下面公式的推导：

$\int_x{\frac{1}{\sigma_1\sqrt{2\pi}}e^{-\frac{(x-\mu_1)^2}{2\sigma_1^2}}x^2dx}=\sigma_1^2+\mu_1^2$

诀窍在于$x^2=(x-\mu)^2+2\mu x-\mu^2$

总之，我们可以得到两个单变量高斯分布的KL散度为： $log \frac{\sigma_2}{\sigma_1}-\frac{1}{2}+\frac{\sigma_1^2+(\mu_1-\mu_2)^2}{2\sigma_2^2}$

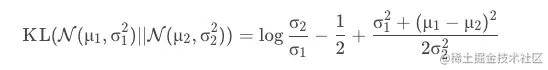
0.3 重参数技巧

VAE当中使用的，如果希望从高斯分布$N(\mu,\sigma)$中进行采样，会造成采样过程不可微分；这时候，我们可以从标准分布$N(0,1)$当中采样出来z，然后利用$\sigma*z+\mu$的方式。这样子可以让采样过程保持可导。

1. VAE

1.1 单层VAE

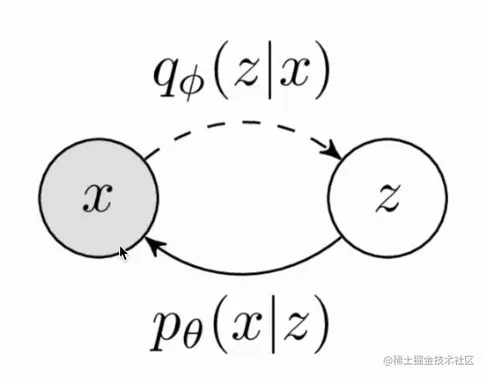
上图是VAE的逻辑，虚线是训练时候的网络模块。将x映射到隐含变量z上，然后再通过z还原x。推理的时候采样z，然后直接从z到x实现生成过程。

简单推导一下VAE的原理：

$p(x)=\int_z p_\theta(x|z)p(z)$

$p(x)=\int_z q_\phi(z|x)*\frac{p_\theta(x|z)p(z)}{q_\phi(z|x)}$ 我们可以写成期望的形式，并且在左边加上log变成对数似然

$logp(x)=logE_{z \sim q_\phi(z|x)}[{\frac{p_\theta(x|z)p(z)}{q_\phi(z|x)}]}$

根据jenson不等式定义，log为上凸函数，所以上公式可以写作：

$logE_{z \sim q_\phi(z|x)}[{\frac{p_\theta(x|z)p(z)}{q_\phi(z|x)}]} \ge E_{z \sim q_\phi(z|x)}log[{\frac{p_\theta(x|z)p(z)}{q_\phi(z|x)}]}$

我们生成图像的目的就是最大化似然，但是这是不可得的。但是我们可以最大化这个似然的下界，所以我们要最大化上面公式右边的东西。

右边的东西我们可以继续推导：

$E_{z \sim q_\phi(z|x)}log[{\frac{p_\theta(x|z)p(z)}{q_\phi(z|x)}]} = E_{z \sim q_\phi(z|x)}log{p_\theta(x|z)} - E_{z \sim q_\phi(z|x)}{\frac{q_\phi(z|x)}{p(z)}}$

后面是KL散度的定义，所以可以下界可以写成：

$E_{z \sim q_\phi(z|x)}log{p_\theta(x|z)} - KL(q_\phi(z|x) || p(z))$

第一项最大化的模型含义就是z生成的x足够真实，第二项需要最小化，物理含义就是要让$q_\phi(z|x)$的分布于$p(z)$相同，都是正态分布。（推导到这里实在是太美了，VAE不愧是GAN之下第一生成模型。）

1.2 多层VAE

经典VAE就是单层VAE，现在我们来看下多层的VAE模型。

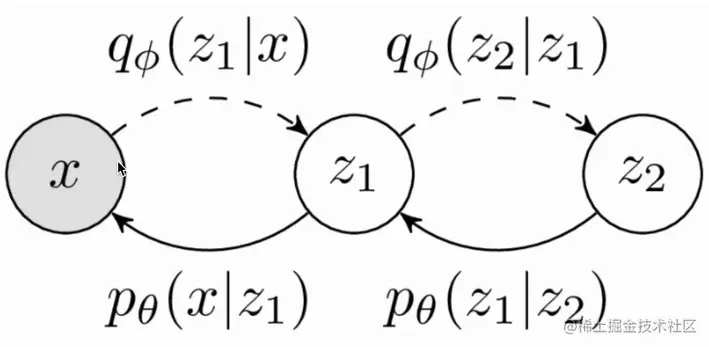
同上，我们来做一个类似的推导：

$p(x)=\int_{z_1}\int_{z_2} p_\theta(x,z_1,z_2)dz_1dz_2$

$p(x)=\int_{z_1}\int_{z_2} q_\phi(z_1,z_2|x) \frac{p_\theta(x,z_1,z_2)}{q_\phi(z_1,z_2|x)}$

$p(x)=E_{z_1,z_2\sim q_\phi(z_1,z_2|x)}{[\frac{p_\theta(x,z_1,z_2)}{q_\phi(z_1,z_2|x)}]}$

$logp(x)=log E_{z_1,z_2\sim q_\phi(z_1,z_2|x)}{[\frac{p_\theta(x,z_1,z_2)}{q_\theta(z_1,z_2|x)}]}\ge E_{z_1,z_2\sim q_\phi(z_1,z_2|x)} log[\frac{p_\theta(x,z_1,z_2)}{q_\phi(z_1,z_2|x)}]$

$p_\theta(x,z_1,z_2)=p_\theta(x|z_1,z_2)p_\theta(z_1|z_2)p(z_2)$

如果服从马尔可夫假设，则：

$p_\theta(x,z_1,z_2)=p_\theta(x|z_1)p_\theta(z_1|z_2)p(z_2)$

$q_\phi(z_1,z_2|x)=q_\phi(z_2|x,z_1)q_\phi(z_1|x)$

如果服从马尔可夫假设，则： $q_\phi(z_1,z_2|x)=q_\phi(z_2|z_1)q_\phi(z_1|x)$

所以最终下界可以表示为：