本文已参与[新人创作礼]活动,一起开启掘金创作之路
转载请注明出处.
图形学的数学基础(二十):几何图元-重心坐标
定义重心坐标(BarycentricCoordinates)
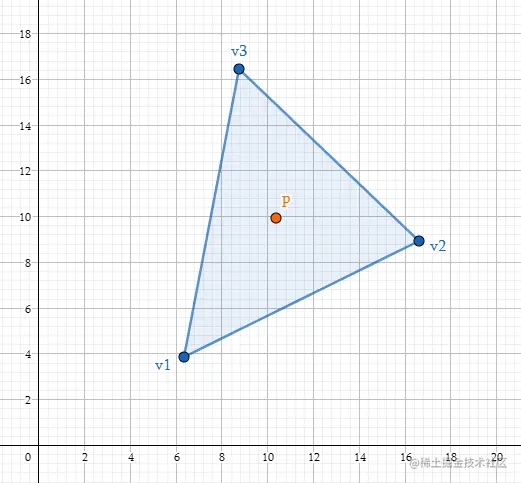
对于空间内的三角形△v1v2v3和任意一点p,必定唯一存在三个数b1,b2,b3,满足:
b1+b2+b3=1
p=b1v1+b2v2+b3v3
则b1,b2,b3就称为p点在此三角形△v1v2v3上的重心坐标.
重心坐标表示了三角形每个顶点对该点的权重(贡献),重心坐标可以用来三角形光栅化顶点的属性插值,比如说uv 颜色 法线的线性插值。
重心坐标也是一种坐标系统,类似于普通笛卡尔坐标系,但有一个区别就是,重心坐标的三个分量之和为1:
b1+b2+b3=1
这种归一化的约束消除了一个自由度,因此即使有三个坐标,它仍然是一个二维空间。
重心坐标不仅适用于三角形内的点,对于边上的点甚至三角形外的点都是适用的,三角形内的重心坐标都是被限制到[0,1]范围内,三角形外的任何点都至少有一个负坐标。
还有一种解释重心坐标的角度,丢弃b3,将(b1,b2)解释为常规的二维坐标,原点位于v3,x轴是v1−v3,y轴是v2−v3
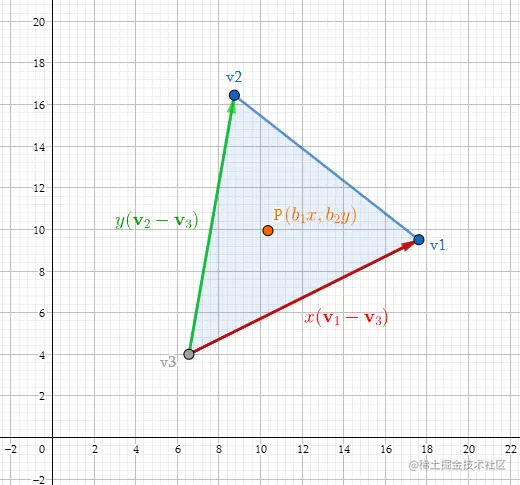
(b1,b2,b3)=>b1v1+b2v2+b3v3=>b1v1+b2v2+(1−b1−b2)v3=>b1v1+b2v2+v3−b1v3−b2v3=>v3+b1(v1−v3)+b2(v2−v3)
计算重心坐标
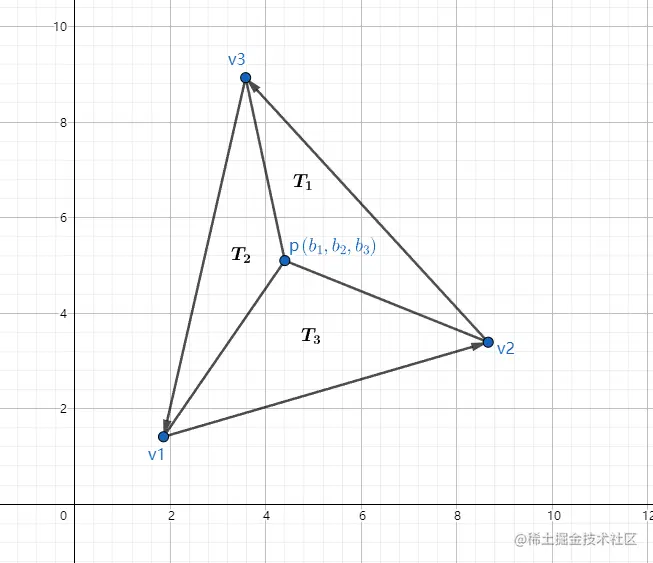
已知p的坐标和v1,v2,v3的顶点坐标,求p的重心坐标(b1,b2,b3),只需要求解线性方程组即可:
⎩⎨⎧b1x1+b2x2+b3x3=pxb1y1+b2y2+b3y3=pxb1+b2+b3=1
求解该方程组得到:
b1=(y1−y3)(x2−x3)+(y2−y3)(x3−x1)(py−y3)(x2−x3)+(y2−y3)(x3−px)
b1=(y1−y3)(x2−x3)+(y2−y3)(x3−x1)(py−y1)(x3−x1)+(y3−y1)(x1−px)
b1=(y1−y3)(x2−x3)+(y2−y3)(x3−x1)(py−y2)(x1−x2)+(y1−y2)(x2−px)
可以看到每个表达式中的分母是相同的,根据三角形的面积公式可得:A=2(y1−y3)(x2−x3)+(y2−y3)(x3−x1),它等于三角形面积的两倍,而且对于每个重心坐标bi来说,其分子等于“子三角形”Ti的面积的两倍:
b1=A(T)A(T1),b2=A(T)A(T2),b3=A(T)A(T3)
因此得出结论:重心坐标等于对面子三角形与大三角形的比例。
所以计算重心坐标可先叉乘计算面积,再求面积比。另外因为公底边三角形面积比等于高(有向高)的比,因此:
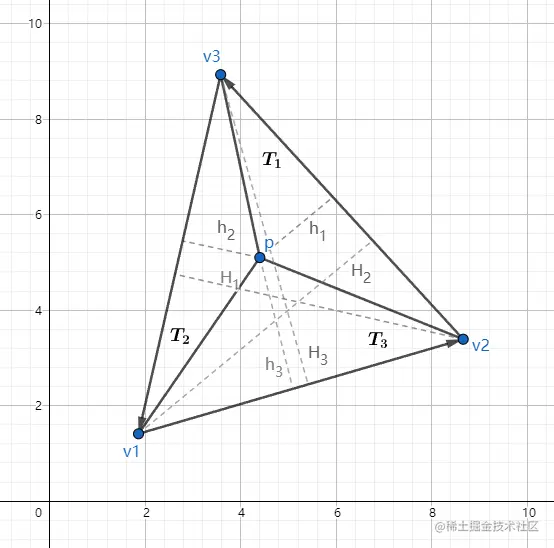
⎩⎨⎧b1=H1h1b2=H2h2b3=H3h3
重心 内心 外心
重心(CenterofGravity)
重心,也称为质心(Centroid),是三角形完美平衡的点。它是中线的交点(中线是从一个顶点到对边中点的直线)。如下图:
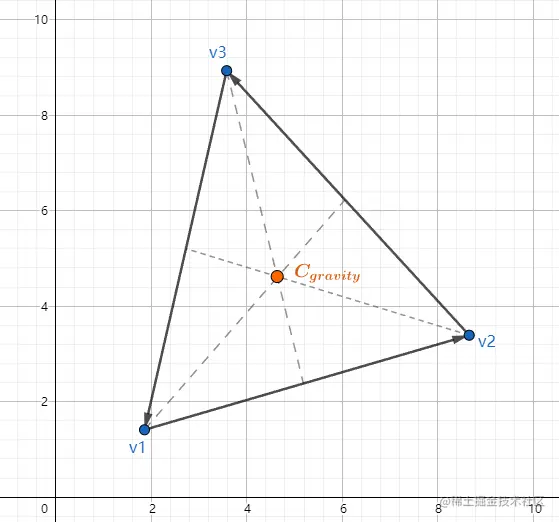
重心是三个顶点的几何平均值:
Cgravity=3v1+v2+v3
重心的重心坐标为:(31,31,31)
内心(Incenter)
内心是三角形三条角平分线的交点。它也是三角形内切圆的圆心。由此可知,内心与三角形各条边的距离是相等的:
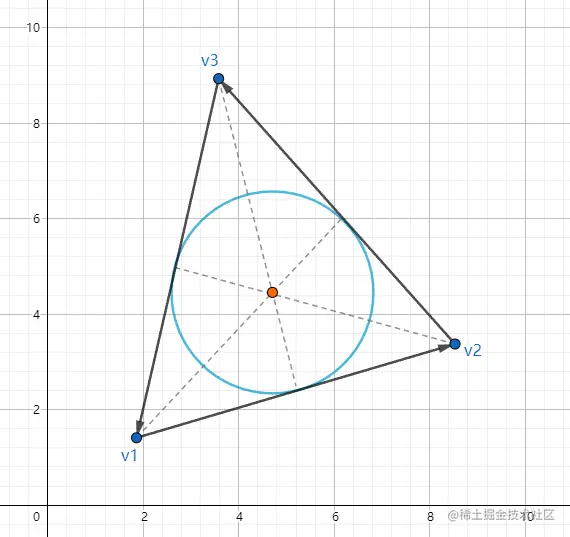
假设P=l1+l2+l3为三角形的周长,l1,l2,l3为每条边长,则内心的重心坐标可是表示为边长与周长比:
(pl1,pl2,pl3)
内心的坐标:
CIncenter=pl1v1+l2v2+l3v3
内切圆半径为三角形面积除以三角形周长:
rIncenter=pA
外心(Circumcenter)
外心是三角形中与顶点等距的点。它是围绕三角形的外接圆的圆心。外心构造为各条边的垂直平分线的交点。
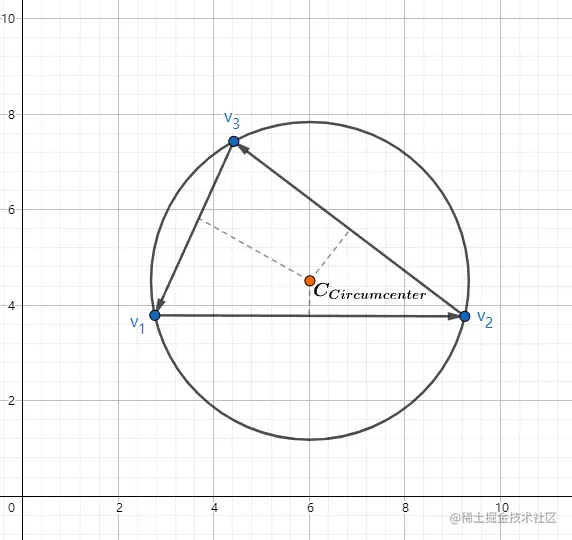
外心的计算
d1=−e2⋅e3
d2=−e3⋅e1
d3=−e1⋅e2
c1=d2d3
c2=d3d1
c3=d1d2
c=c1+c2+c3
外心重心坐标:(2cc2+c3,2cc3+c1,2cc1+c2)
外心坐标:CCircumcenter=2c(c2+c3)v1+(c3+c1)v2+(c1+c2)v3
外接圆半径:rCircumcenter=2(d1+d2)(d2+d3)(d3+d1)
参考
《3D数学基础》图形和游戏开发(第二版)