本文已参与[新人创作礼]活动,一起开启掘金创作之路

图形学的数学基础（十八）：几何图元-平面(下)

转载请注明出处

上章推导了平面方程的定义。这章介绍几种和平面有关的常见求交和计算点到平面距离的方法。

平面距原点的最短（垂直）距离

如果平面的法线是单位矢量,则平面方程的常数项$d$是原点到平面的有符号距离。

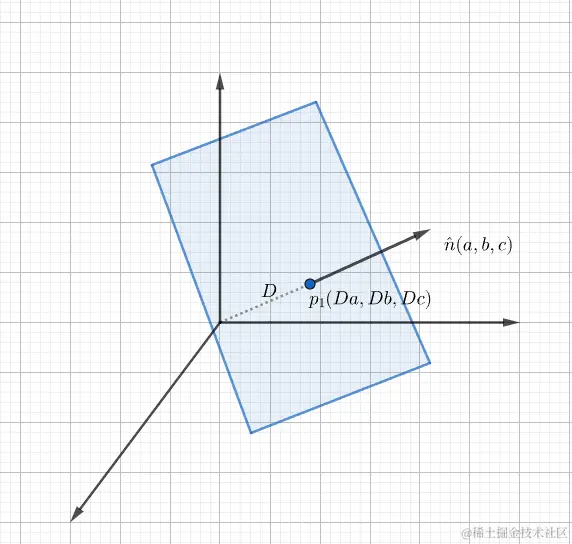
假设单位矢量$\hat{n}$ $\begin{bmatrix}a\\ b\\ c\\ \end{bmatrix}$,则平面上的一点$\textbf{P}_1$可以写成$\begin{bmatrix}Da\\ Db\\ Dc\end{bmatrix}$的形式，D是从原点到平面的垂直有符号距离。因此我们可以将平面方程重写如下：

$\begin{bmatrix}a\\ b\\ c\\\end{bmatrix}\cdot\begin{bmatrix}x-Da\\ y-Db\\ z-Dc\\\end{bmatrix} = 0$

$a(x-Da) + b(y-Db) + c(z-Dc) = 0$

$ax + by + cz -D(a^2 + b^2 + c^2) = 0$

$ax + by + cz -D||\vec{n}|| = 0$

因此原点到平面的垂直有符号距离 $D = \dfrac{d}{||\vec{n}||}$,其中$\textbf{d}$为平面方程的常数项。

任意点到平面的最短（垂直）距离

很多时候我们可能会有一个平面和一个不在平面内的点$\textbf{q}$，然后想要计算从该平面到$\textbf{q}$的距离。如果该距离为负数，则$\textbf{q}$在平面的背面，反之在正面。为此我们假设平面中的一个点$\textbf{p}$，它是该平面中与$\textbf{q}$最近的点，显然从$\textbf{p}到\textbf{q}$的矢量垂直于平面，因此它是$a\vec{n}$的另外一种形式。

对于平面$ax + by + cz+d = 0$，任意一点$\textbf{q}$到平面的最短距离推导如下：

$\textbf{p} + a\vec{n} = \textbf{q}$

$(\textbf{p} + a\vec{n})\cdot\vec{n} = \textbf{q}\cdot\vec{n}$

$\textbf{p}\cdot\vec{n} + a\vec{n}\cdot\vec{n} = \textbf{q}\cdot\vec{n}$

$d||\vec{n}|| + a||\vec{n}||^2 = \textbf{q}\cdot\vec{n}$

$d||\vec{n}|| + a||\vec{n}||^2 = \textbf{q}\cdot\hat{n}||\vec{n}||$

$d + a||\vec{n}|| = \textbf{q}\cdot\hat{n}$

$a = \dfrac{\textbf{q}\cdot\hat{n} - d}{||\vec{n}||}$

对于单位矢量则有：

$a = \textbf{q}\cdot\hat{n} - d$

求解三平面的交点

求解三平面相交交点，我们只需要解三个平面方程组成的线性方程组即可：

$\begin{cases} a_1x+b_1y+c_1z + d_1 = 0\\ a_2x+b_2y+c_2z + d_2 = 0\\ a_3x+b_3y+c_3z + d_3 = 0\\ \end{cases}$ 可以写成矩阵的形式：

$\begin{bmatrix} a_1&b_1&c_1\\ a_2&b_2&c_2\\ a_3&b_3&c_3\\ \end{bmatrix}\begin{bmatrix} x\\ y\\ z\\ \end{bmatrix} = \begin{bmatrix} -d_1\\ -d_2\\ -d_3\\ \end{bmatrix}$

平面直线相交

空间中的平面和直线可能会相较于某一点，交点可以通过平面和直线的线性方程组求解：

$\begin{cases} \textbf{Plane} & ax+by+cz+d = 0\\ \textbf{Line} & \textbf{p}_1 + t\vec{v} = (x_1+tv_x,y_1+tv_y,z_1+tv_z) \end{cases}$

$t = \dfrac{-(ax_1+by_1+cz_1+d)}{av_x+bv_y+cv_z}=\dfrac{-(\vec{n}\cdot\textbf{p}_1+d)}{\vec{n}\cdot\vec{v}}$

克莱默法则（$Cramer's\;Rule$）

克莱默法则，用于求解具有n个线性方程的方程组。

$\begin{cases} a_{11}x_1+a_{12}x_2 +...+ a_{1n}x_n = b_1\\ a_{21}x_1+a_{22}x_2 +...+ a_{2n}x_n = b_2\\ .........................................\\ a_{n1}x_1+a_{n2}x_2 +...+ a_{nn}x_n = b_n \end{cases}$

若线性方程组的系数行列式不等于0，即$\det{A} =\begin{vmatrix} a_{11}...a_{1n}\\ ............\\ a_{n1}...a_{nn}\\ \end{vmatrix} != 0$

则线性方程组的解可以用行列式来表示：

$x_1 = \dfrac{\det{A_1}}{\det{A}}, x_2 = \dfrac{\det{A_2}}{\det{A}}, x_n = \dfrac{\det{A_n}}{\det{A}}$

其中$\det{A_n}$是把行列式$\det{A}$中第n列的所有元素，依次用方程组右端的常数项替换。

求解线性方程组

根据克莱默法则，可知：

$x = \dfrac{\det{A_x}}{\det{A}},y = \dfrac{\det{A_y}}{\det{A}},z = \dfrac{\det{A_z}}{\det{A}}$

$\det{A} = \begin{vmatrix} a_1&b_1&c_1\\ a_2&b_2&c_2\\ a_3&b_3&c_3\\ \end{vmatrix}$

$\det{A_x} = \begin{vmatrix} -d_1&b_1&c_1\\ -d_2&b_2&c_2\\ -d_3&b_3&c_3\\ \end{vmatrix},\det{A_y} = \begin{vmatrix} a_1&-d_1&c_1\\ a_2&-d_2&c_2\\ a_3&-d_3&c_3\\ \end{vmatrix},\det{A_z} = \begin{vmatrix} a_1&b_1&-d_1\\ a_2&b_2&-d_2\\ a_3&b_3&-d_3\\ \end{vmatrix}$

$p = \dfrac{-d_1(\vec{n_2}\times\vec{n_3}) -d_2(\vec{n_3}\times\vec{n_1})-d_3(\vec{n_1}\times\vec{n_2})}{\vec{n_1}\cdot(\vec{n_2}\times\vec{n_3})}$

求两平面相交的直线方程

两个非平行平面会相交与一条线，直线方程可以用一个方向矢量$\vec{v}$和一个点$\textbf{p}_o$来表示：$\textbf{p}_o + t\vec{v}$, $\vec{v}$垂直于两个平面的法线$\vec{n_1}和\vec{n_2}$，因此$\vec{v} = \vec{n_1}\times\vec{n_2}$

现在需要找到直线上的任意一点$\textbf{p}_o$,根据上节内容，三个平面相交于一点，因此我们只需要构造出第三个平面（法线为$\vec{v}$并且d = 0），因此第三个平面方程为：

$v_xx+v_yy+v_zz = 0$

根据上节三平面求交点公式：

$\textbf{p}_o = \dfrac{-d_1(\vec{n_2}\times\vec{n_3}) -d_2(\vec{n_3}\times\vec{n_1})-d_3(\vec{n_1}\times\vec{n_2})}{\vec{n_1}\cdot(\vec{n_2}\times\vec{n_3})}$

$\textbf{p}_o = \dfrac{-d_1(\vec{n_2}\times\vec{v})-d_2(\vec{v}\times\vec{n_1})}{\vec{n_1}\cdot(\vec{n_2}\times\vec{v})}$

$\textbf{p}_o =\dfrac{(-d_1\vec{n_2} + d_2\vec{n_1})\times\vec{v}}{\vec{v}\cdot\vec{v}}$

$\textbf{Line} = \textbf{p}_o + t\vec{v}\\ = \dfrac{(-d_1\vec{n_2} + d_2\vec{n_1})\times\vec{v}}{\vec{v}\cdot\vec{v}} + t\vec{v}$

参考

《3D数学基础》图形和游戏开发(第二版)

songho-openGL

克莱默法则