跳跃搜索算法用于在一个排序的数组中搜索一个元素。跳跃搜索或块搜索通过在每一步中跳过/跳过固定数量的元素来搜索排序数组中的一个元素。通过这种方式,跳跃搜索比线性搜索检查的元素更少。
跳跃搜索算法的表现比线性搜索好,但不比二进制搜索好,而且这只对排序数组有效。
1.跳跃搜索是如何工作的?
在跳转搜索中,我们遍历排序后的数组,并以特定的块大小向前跳转。我们将通过获取数组大小的平方根来确定跳转的块大小,即√n,其中n是排序后数组的长度。
当我们找到一个大于搜索元素的元素时,在当前块中进行线性搜索。如果该元素存在于数组中,就会在该块中找到。
由于跳转搜索在搜索操作中使用块,它也被称为块搜索算法。
1.1.算法步骤
让我们了解一下步骤的顺序。
- 对数组进行排序,如果尚未排序。
- 计算要跳跃的块大小。一般来说,它是数组长度的平方根。
- 遍历排序后的数组,根据计算出的块大小跳转元素。
- 当当前值大于给定值时,执行线性搜索。
- 一旦找到匹配的元素,返回该元素的索引。
1.2.跳跃搜索实例
让我们通过一个例子来理解。我们有10,20,30,40,50,60,70,80,90个元素,我们正在搜索60个元素。在我们的例子中,数组是排序的,所以我们可以跳过它。
计算要跳跃的块的大小,即 **√**9 = 3.所以我们将遍历给定的排序数组,每次跳过3个元素。
在每一步,我们将比较当前元素值和搜索元素。如果当前元素小于搜索元素,继续跳到下一个块。如果当前元素大于搜索元素,那么从上一步元素到当前步骤元素进行线性搜索。
在我们的例子中,我们从索引0开始搜索元素60,跳到索引3,然后跳到索引6。当我们发现当前在索引6的元素是70,并且它大于当前值60。于是我们开始从上一个索引(3)到当前索引(6)搜索元素。
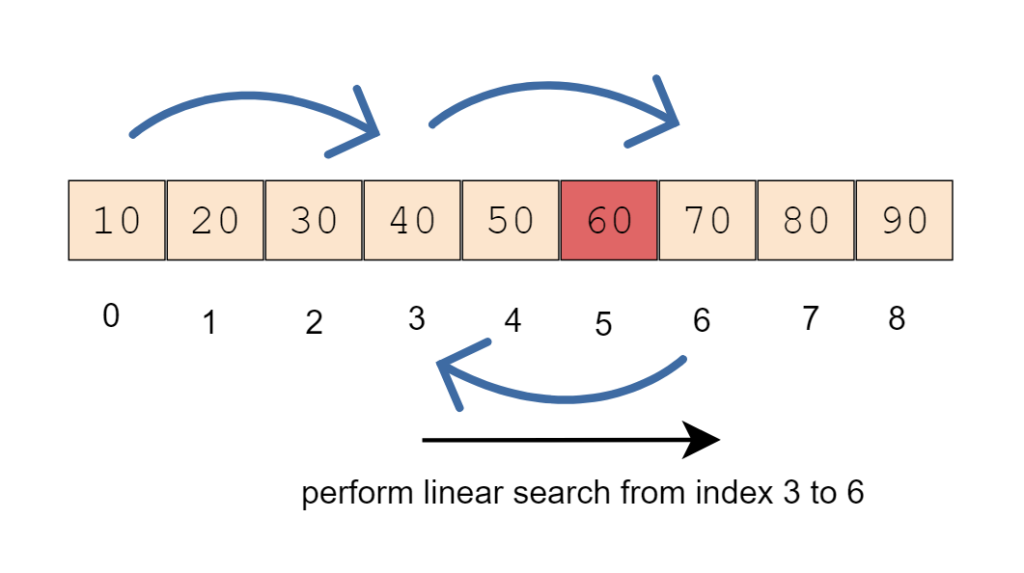
一旦找到匹配的元素,我们将返回该元素的索引。
2.在Java中实现跳转搜索
在下面的例子中,我们是:
- 声明并初始化排序的数组
arr和搜索元素ele。 - 计算数组的长度并将其分配给变量
n。 - 计算要跳转的块/步的大小并将其分配给变量
step。 - 定义
jumpSearch(),该函数接受一个数组、搜索元素、数组长度和步长作为参数。如果找到一个匹配的元素,它将返回该元素的索引;否则返回-1。 - 在变量prev中存储前一步。
- 遍历数组,直到当前元素小于给定元素。
- 使用线性搜索算法遍历数组,从prev的索引元素到给定的元素,如果找到一个匹配的元素,我们将返回该元素的索引;否则返回-1。
public class JumpSearchAlgorithm {
public static void main(String[] args) {
int[] arr = {10, 20, 30, 40, 50, 60, 70, 80, 90};
int ele = 60;
int foundIndex = jumpSearch(arr, ele);
System.out.println(foundIndex > 0 ? "Found at index : " + foundIndex : "Element Not Found");
}
public static int jumpSearch(int[] arr, int ele) {
int prev = 0;
int n = arr.length;
int step = (int) Math.floor(Math.sqrt(n));
//loop until current element is less than the given search element
while (arr[Math.min(step, n) - 1] < ele) {
prev = step;
step += (int) Math.floor(Math.sqrt(n));
if (prev >= n) return -1;
}
//perform linear search prev index element to given element
while (arr[prev] < ele) {
prev++;
if (prev == Math.min(step, n)) return -1;
}
// Return index if element is found
if (arr[prev] == ele) return prev;
return -1;
}
}
Found at index : 5
3.时间和空间复杂度
3.1 时间复杂度
跳跃搜索算法的时间复杂度为O(√n)。
3.2.空间复杂度
由于我们没有创建任何其他的临时数据结构,跳转搜索算法的空间复杂度为O(1) 。
4.总结
在本教程中,我们学习了跳转搜索算法,并通过一个例子理解了它。这个算法只适用于排序的数组,表现比线性搜索好,但不超过二进制搜索。
学习愉快