深入浅出 Pytorch 系列 — 优化器的选择(2) Adagrad 、MSProp 和 adam携手创作，共同成长！

携手创作，共同成长！这是我参与「掘金日新计划 · 8 月更文挑战」的第16天，点击查看活动详情

我们 loss 函数曲面是崎岖不平，有相对平缓的区域，也有陡峭的区域，那么如果在整个梯度下降过程中如果都采用一个步长(学习率)都会有问题的。

如果学习率设置过大那么就很容出现下图左图现象，当接近极值点，因为学习率过大会始终在极值点附近震荡无法抵达到极值点。

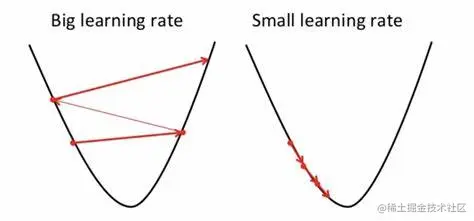
那么如果设置过小，就会导致训练起来时间比较长。甚至难以接受，所以我们就需要根据不同 loss 曲面来调整学习率

翻译过来是自适应梯度，听起来很酷名字，那么 AdaGrad 出现又是来解决什么样问题呢? 有的时候我们loss 不再下降，但是梯度 norm 并不是 0，这是有可能梯度在距离极值点有段距离的山谷处震荡。

\theta^{t+1} = \theta^{t} - \frac{\eta}{\sqrt{\sum_{i=0}^{t} (g^i)^2}} g^{t}

AdaGrad 适合处理稀疏数据，那么什么是稀疏数据呢? 我们知道数据维度就是数据特征，通过特征是否存在来进行分类，那么通常这样数据集就是稀疏数据集。而如果通过数据某一个特征量多少来进行判断通常这样特征就是稠密特征。

不同参数具有不同梯度，

Adagrad 适合稀疏数据，那么什么样数据算是稀疏数据呢?通过特征不同，而不是通过特征量来区分，

这里 RMSProp 与 Adagrad 不同之处，就是计算累积梯度平方方式不同，在 RMSProp 中并没有采用 Adagrad 那样直接累加梯度平方，而是通过一个衰减系数来控制历史梯度信息对当前影响程度

\sigma^0 = g^0\\ \theta^1 = \theta^0 - \frac{\eta}{\sigma^0} g^0

\sigma^1 = \alpha \sigma^0 + (1 - \alpha)g^1\\ \theta^2 = \theta^1 - \frac{\eta}{\sigma^1} g^1

\sigma^t = \alpha \sigma^{t-1} + (1 - \alpha)g^t\\ \theta^t = \theta^{t-1} - \frac{\eta}{\sigma^t} g^t

简单总结一下，就是在设置了全局学习率后，每次通过全局学习率除以一个经过衰减系数控制历史梯度平方和平方根，来不断调整每个参数的梯度。起到的效果是在参数空间更为平缓的方向，会取得更大的进步（因为平缓，所以历史梯度平方和较小，对应学习下降的幅度较小），并且能够使得陡峭的方向变得平缓，从而加快训练速度。

在 BERT 和 Transformer 中才采用 Adam 作为优化器。这是因为 adam 优先器实现比较容易，并且占用内存比较少，对于梯度对角缩放具有不变性，而且参数直观具有可解释性。适用于非常嘈杂或稀疏梯度的问题，适合非平稳和非凸优化问题。

Adam 适合高维空间随机优化目标的问题，高维数据给优化问题来带了一定程度上复杂性。对于 Adam 算法来说，仅用一阶梯度占用比较少内存就可以取得不错的效果。其实把 RMSProp 和 SGDM 这两种方法结合的产物。

数学中矩概念和物理中矩的概念是相通的， $r^nQ$ 某一个量到参考点 n 次方，物理力就是一阶矩。二阶矩也是惯性是旋转方向的惯性，那么一阶矩是物体保持直线运动的动量，而二阶矩是保持静止或圆周运动的动量。

g^2_t = g_t g_t

关于 Adam 实现步骤，从 t-1 时刻或者步骤到 t 时刻，求解参数 $\theta$ 的梯度

g_t = \nabla_{\theta} f_t(\theta_{t-1})

然后更新一阶矩 $m_t$ 和二阶矩 $v_t$

m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t\\ v_t = \beta_2 v_{t-1} + (1 - \beta_2) g^2_t

接下里是对 $m_t$ 和 $v_t$ 的一个校正，这是对初期平滑偏差较大的一个修正，叫做 bias correction，当 $t$ 越来越大， $1- \beta_1^t$ 和 $1 - \beta_2^t$ 就越趋近于 1

\hat{m}_t = m_t/(1 - \beta_1^t)\\ \hat{v}_t = v_t/(1- \beta_2^t)

\theta_{t} = \theta_{t-1} - \alpha \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon}

主要用来一阶矩和二阶矩，更新参数过，一阶矩控制动量，二阶矩左右旋转，指数衰减，开始快后来逐渐减速。Adam 对步长，步长的有界性

g_{t} = \nabla \hat{L}(\theta_{t}) \\ m_{t} = \beta_{1} m_{t-1} + (1-\beta_{1}) g_{t} \\ v_{t} = \beta_{2} v_{t-1} + (1-\beta_{2}) g_{t}^{2} \\

\hat{m}_{t} = \frac{m_{t}}{1-\beta_{1}^{t}} \\ \hat{v}_{t} = \frac{v_{t}}{1-\beta_{2}^{t}} \\ \theta_{t+1} = \theta_{t} -

\frac{\eta}{\sqrt{\hat{v}_{t}} + \epsilon} \hat{m}_{t}

并且这个优化器具有可解释性。在机器学习许多问题都可以转为求标量的优化问题，也就是我们用标量做优化指标，也就是转换为求最大化或者最小化的问题。

在求解全局最大或最小值过程会遇到许多问题例如，局部最小值、鞍点、平坦区域和悬崖等给梯度下降造成困难的区域。

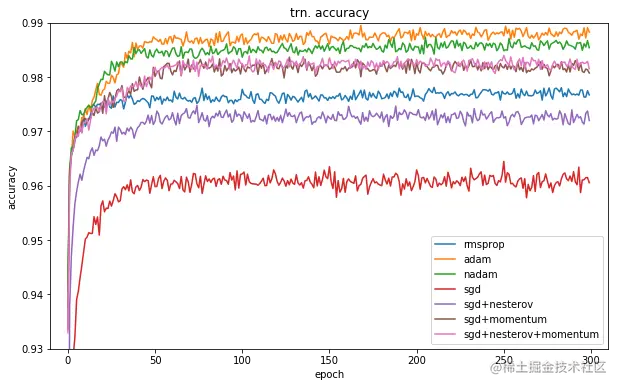
我们注意看这张图，通过一个分类训练通过使用不同分类器对比试验，不难发现 adam 在训练集很快就冲到了前面，而 sgdm 之中位于中上游的位置。

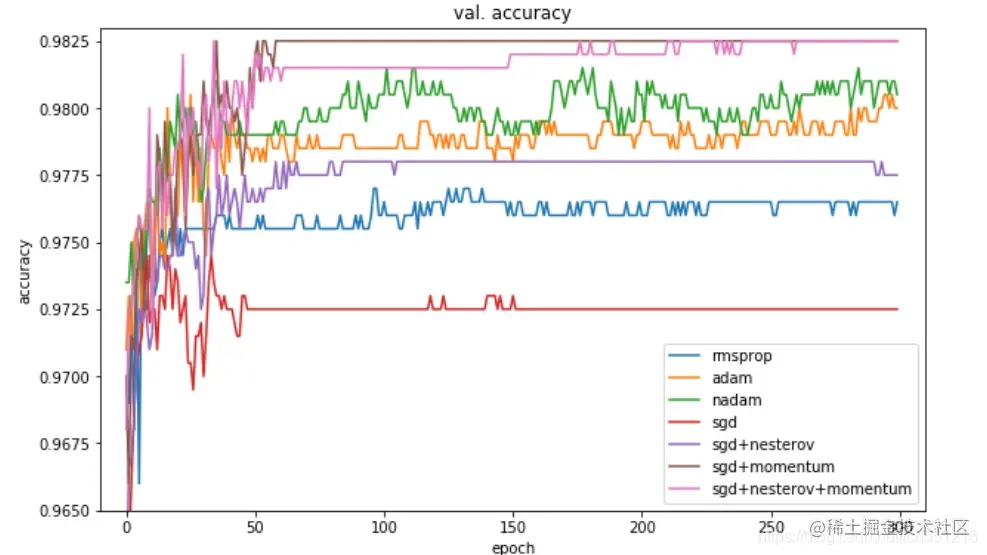
这张图是一个验证阶段，从这张图来看，在验证集上，SGDM 很快就冲到前面，而 adam 在验证集上表现并不是很稳定，一直上下起伏。