基于Smith预估器补偿系统控制延迟和传感器延迟(附Matlab实现)

努力学习的小伟同学
293 阅读3分钟

携手创作，共同成长！这是我参与「掘金日新计划 · 8 月更文挑战」的第2天

前言

实际设计控制器时，不可避免会有延迟，包括控制延迟和传感器延迟，当延迟比较大时，可能会造成控制器失稳。因此在控制器设计时，需要考虑延迟的影响。这个问题在网络控制系统(Networked Control system)尤为普遍，相应的解决方法也有很多。文章采用一个简单经典的解决办法——Smith预估补偿，先介绍原理，再在Simulink中实现

Smith 预估补偿原理

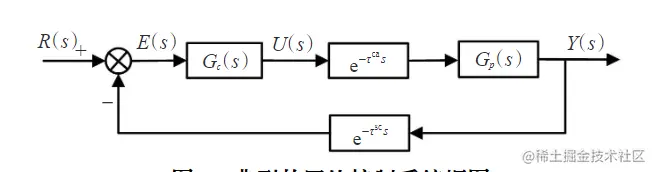
一个典型的控制环节如图1所示， 请添加图片描述

图1： 典型控制系统

系统延迟包括控制延迟τca\tau^{ca}和传感器延迟\rausc\rau^{sc}闭环传递函数为：

Y(s)R(s)=Gc(s)Gp(s)e−τcas1+Gc(s)Gp(s)e−τscse−τcas\frac{Y(s)}{R(s)}=\frac{G_{c}(s) G_{p}(s) \mathrm{e}^{-\tau^{c a_{s}}}}{1+G_{c}(s) G_{p}(s) \mathrm{e}^{-\tau^{sc}s} \mathrm{e}^{-\tau^{\mathrm{ca} }s}}

这里执行器以一阶系统为例，其传递函数为： Gp(s)=1s+1G_p(s)=\frac{1}{s+1} 采用PID算法，器传递函数为：

Gc(s)=Kp((KdKp)s2+s+(KiKp))s=Kp(Tds+1+1Tis)G_{c}(s)=\frac{K_{\mathrm{p}}\left(\left(\frac{K_{\mathrm{d}}}{K_{\mathrm{p}}}\right) s^{2}+s+\left(\frac{K_{\mathrm{i}}}{K_{\mathrm{p}}}\right)\right)}{s}=K_{\mathrm{p}}\left(T_{\mathrm{d}} s+1+\frac{1}{T_{\mathrm{i}} s}\right)

其中，Kp,Td,TiK_p,T_d,T_i分别为比例增益，微分时间常数和积分时间常数。选取控制器参数为Kp=17.2,Td=0;Ti=0.2K_p=17.2,T_d=0;T_i=0.2。

在系统中引入Smith估计器减少延迟的影响，控制框图如图2所示： 图2 图2：Smith predictor结构

图中τp\tau_p为系统总延迟，有τp=τca+τsc\tau_p=\tau^{ca}+\tau^{sc}。Gp′(s)e−τp′sG_{p}^{\prime}(s) e^{-\tau_{p}^{\prime} s}为引入的预估补偿传递函数。该结构的系统闭环传递函数为：

Y(s)R(s)=Gc(s)Gp(s)e−τcas1+Gc(s)Gp′(s)+Gc(s)(Gp(s)e−τps−Gp′(s)e−τp′s)\frac{Y(s)}{R(s)}=\frac{G_{c}(s) G_{p}(s) e^{-\tau^{ca} s}}{1+G_{c}(s) G_{p}^{\prime}(s)+G_{c}(s)\left(G_{p}(s) e^{-\tau_{p} s}-G_{p}^{\prime}(s) e^{-\tau_{p}^{\prime} s}\right)}

当不存在模型失配，即Gp′(s)=Gp(s),τp′=τpG_p^{\prime}(s)=G_{p}(s),\tau_{p}^{\prime}=\tau_{p}，系统闭环传递函数简化为： Y(s)R(s)=Gc(s)Gp(s)1+Gc(s)Gp(s)e−τcas\frac{Y(s)}{R(s)}=\frac{G_{c}(s) G_{p}(s)}{1+G_{c}(s) G_{p}(s)} e^{-\tau^{ca} s}

观察可以发现，此时系统与没有延迟的系统相比，传递函数只是多乘上了e−τcase^{-\tau^{ca} s}。也就相当于闭环回路中不含滞后项，滞后环节也不会影响系统的特征方程，此时系统简化图如图3所示。也就是说经过Smith预测补偿后的系统与无延迟的系统相比，只是将控制过程推迟了时间e−τcase^{-\tau^{ca} s}。

在这里插入图片描述

图3： 简化后系统模型

Matlab实现

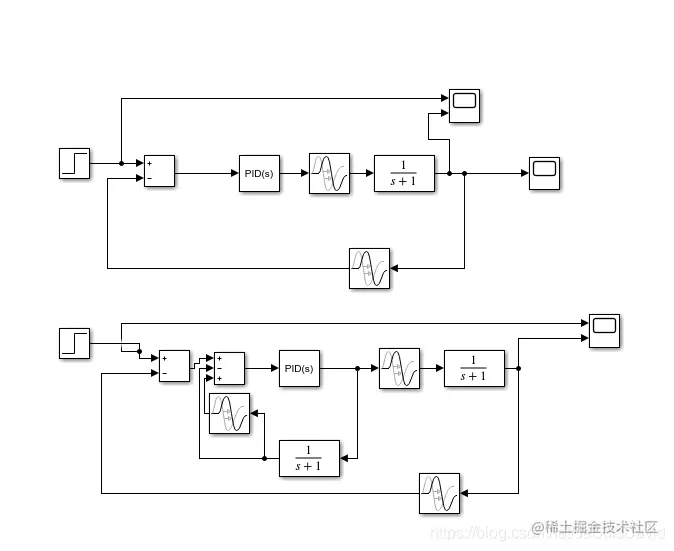
在Simulink中把加smith补偿和没加的都搭出来方便对比。由于比较简单，就不过多赘述，直接上图。 在这里插入图片描述

图4：Simulink实现

设置控制延时和传感器延时均为0.05s，仿真结果如图5所示。可以看到未加smith补偿的控制系统(左图)已经失稳，而加上smith补偿的控制系统的响应时稳定，只是有了0.05s的滞后。 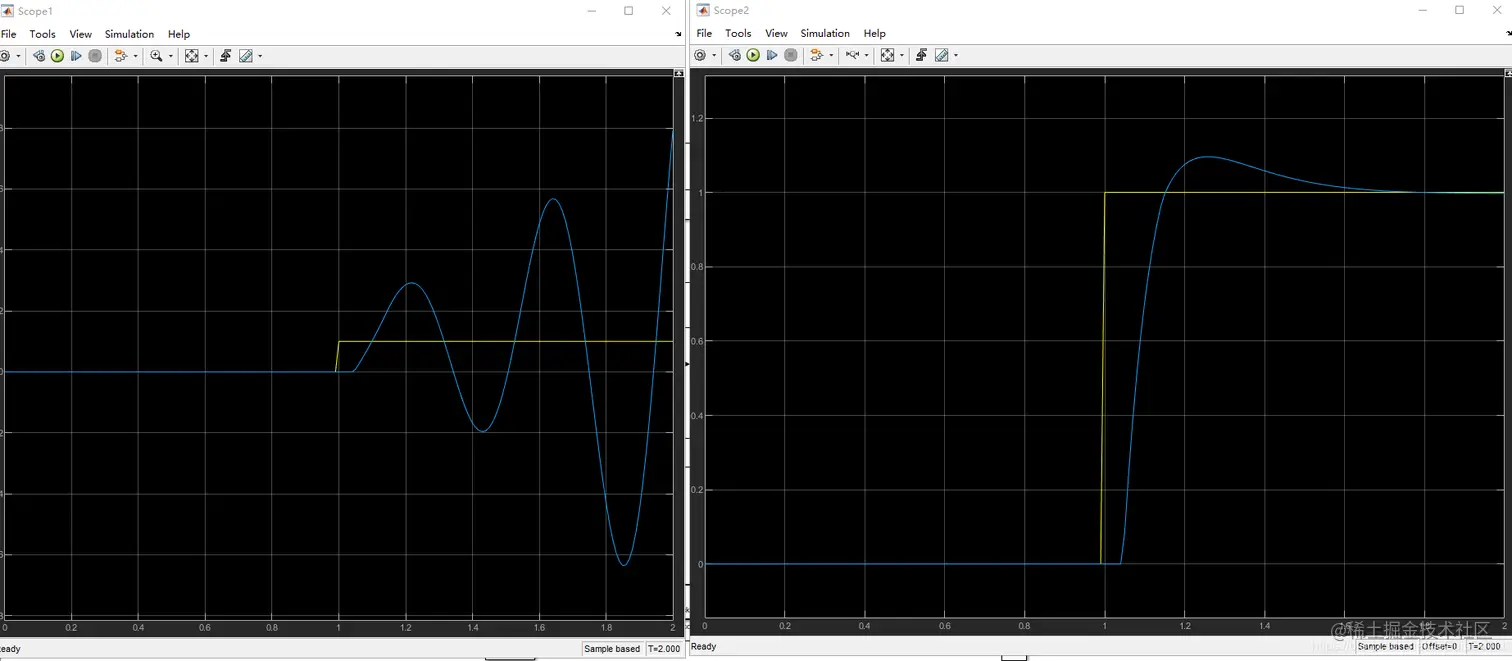在这里插入图片描述 图5：两个模型节约二响应(左图：未加smith补偿，右图：添加smith补偿)

总结

由于上述的Smith 预估补偿器是建立在被控对象和网络延迟的精确数学模型之上，而在实际应用中，延迟有可能是随机的，并且Smith 预估模型可能存在扰动，使其不能完全和被控对象模型相匹配，因此这个方法的鲁棒性不强。改进方案也有很多，大致可以分为结构改进和参数整定两类，具体可以参考我下最后列出来的论文。

另外，除了Smith补偿控制，也有很多其他的方法，比如随机最优控制方法，增广状态确定性离散事件模型方法，缓冲队列方法等等。

参考文献

[1]张海涛,李珍.基于Smith预估补偿的网络控制系统仿真研究[J].计算机工程与应用,2012,48(08):243-245. [1]李珍. 网络化控制系统的延迟补偿研究[D].河南科技大学,2011.

avatar
文章
阅读
粉丝