本文已参与「新人创作礼」活动,一起开启掘金创作之路。
一种新的优化方法:海豚回声定位
海豚回声定位算法(Dolphin echolocation,DE)由伊朗人A. Kaveh和N. Farhoudi于2013年提出,是一种新型的元启发式优化算法,其模拟了海豚在捕食过程中利用回声定位的策略。
回声定位
海豚可以发出滴答滴答的声音,这些滴答声的频率远远高于交流信号的频率。当声音撞击到物体,声波的部分能量会反射回海豚身上,海豚接收到回声后会发出另一种滴答声,海豚会根据滴答声与回声之间的时间间隔评估出与物体的距离,还会根据头部两侧接收到的不同强度的信号进行方向判断,通过不断地发出滴答声和接受回声,海豚可以跟踪并锁定目标。当海豚接近感兴趣的目标时,还会提高滴答的速率。
尽管蝙蝠也是利用回声定位,但是它们却与海豚的声纳系统不同。蝙蝠声纳系统的范围较小,一般3到4米左右,而海豚能探测到的目标范围从几十米到一百多米不等。声波在空气中的传播速度大约是水传播速度的五分之一,因此蝙蝠在声纳传播过程中的信息传递速度要比海豚短得多。这些在环境和猎物方面的不同就需要不同类型的声纳系统,从而很难直接比较出孰好孰坏。
对于优化问题,海豚利用回声定位的原理捕食猎物的过程类似于寻找问题的最优解。初始时,海豚对整个空间进行搜索以寻找猎物,随着越来越接近目标,海豚就会缩小搜索范围,并增加滴答声以专注于某一位置。
该算法通过限制与目标距离成比例的探索来模拟回声定位,分为两个阶段:第一阶段,算法探索整个空间以进行去全局搜索,因而可以搜寻未曾探索过的区域,主要是通过随机探索位置来实现;第二阶段,算法将围绕前一阶段中获得的较优结果附近进行开发利用。
使用海豚回声定位算法时,用户可以根据预定义的曲线改变阶段1与阶段2产生解的比率。在用户定义的这条曲线上应该保证优化收敛,算法然后设置参数以便遵循这条曲线。与其他方法相比,该方法与最优解出现的可能性相关,换句话说,对于每个变量,在可行域内都有不同的可选值,在每个循环中,算法根据用户确定的收敛曲线,定义了选择到目前为止实现的最优值的可能性,利用这条曲线,使算法的收敛性得到控制,从而降低对参数的依赖性。
回声定位算法
在开始优化之前,需要对搜索空间按以下规则进行排序:
搜索空间排序:对于每个变量,对搜索空间的可选值按升序或降序排序,如果可选值包含多个特征,则按最重要的进行排序。对于变量j,所有的可选值构成了长度为LAj的向量Aj,将这些向量作为列就得到了矩阵AlternativesMA×NV,其中MV为max(LAj)j=1:NV,NV为变量个数。
优化过程中收敛因子应根据曲线进行改变,曲线定义如下:
P P\left(L o o p_{i}\right)=P P_{1}+\left(1-P P_{1}\right) \frac{L o o p_{i}^{\text {Power }}-1}{(\text {LoopsNumber})^{\text {Power}}-1}\tag{1}
其中PP为预定义的概率,PP1为第一次循环时的收敛因子,在第一次循环中随机选择解。Loopi为当前循环数,Power为曲线度。
循环数:算法达到收敛点的循环数,这个参数应该根据计算量由用户选择。
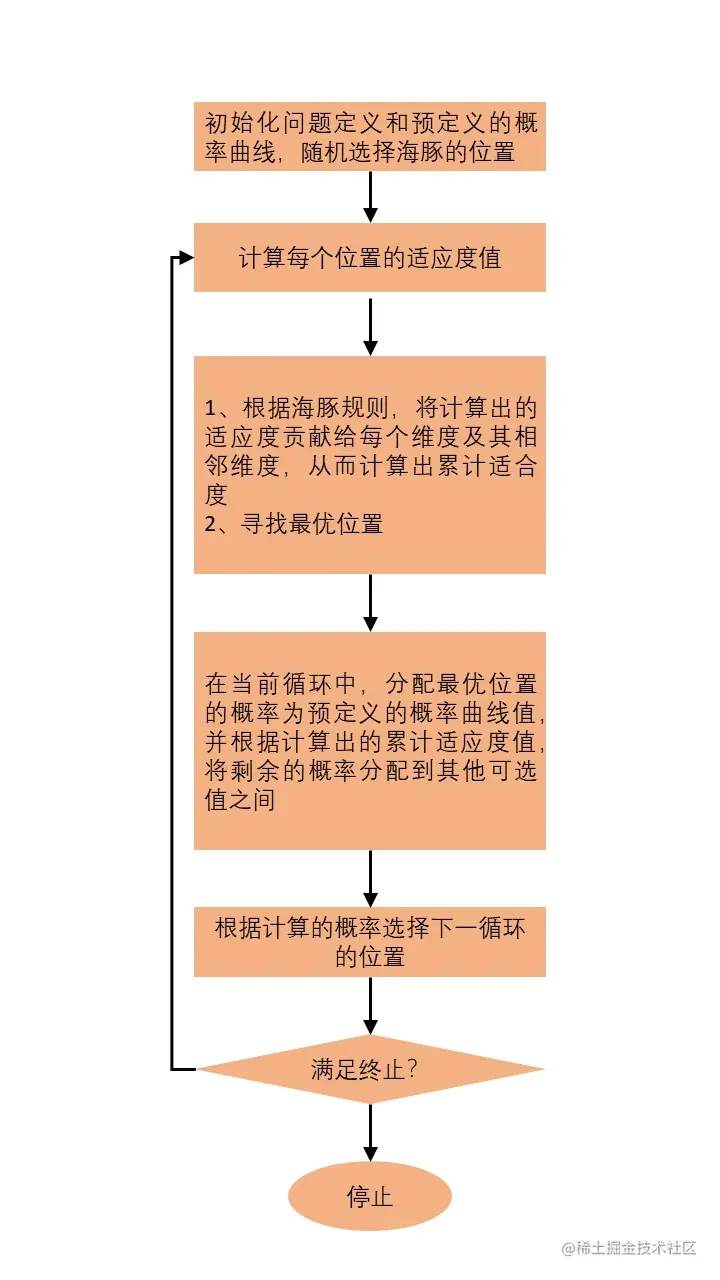
算法的流程图如下图所示,以下面的优化问题为例,说明海豚回声定位的主要步骤。
\min \left(h=\sum_{i=1}^{N} x_{i}^{2}\right), \quad x_{i} \in Z,-20 \leqslant x_{i} \leqslant 20\tag{2}
其中N=4。
在算法优化之前,首先根据等式(1)选择曲线,其中Power=1,循环数Loops number=8,以及PP10.1,则由
P P=0.1+0.9\left(\frac{\text {Loop}_{i}-1}{7}\right)=0.1+0.9\left(\text {Loop}_{i}-1\right)\tag{3}
- 随机初始化NL个海豚位置。
这一步主要包括创建LNV×NV,其中NL为位置个数,NV为变量个数(每个位置的维度)。对于该实例,考虑NL=30,NV=4,每个维度取值均在[-20,20]之间,第i位置的解可能为Li=10,4,−7,18。
- 根据等式(1)(对于该例子就是等式(3))计算循环的PP。
- 计算每个位置的适应度值。
在该例中,式(2)定义了目标函数,如对于位置Li,h=(−10)2+42+(−7)2+182=489。在海豚回声定位算法中,适应度值用于计算概率,较优的适应度值应该具有更高的概率,因此对于对于最小化问题则适应度应该为目标值的相反数,即Fitness=1/h。为了避免除以0,通常使用Fitness=1/(h+1),在该例中,Fitness(Li)=1/(489+1)=0.00204。
- 根据如下的海豚规则计算累积适应度值:
(a)
for i=1 to 可选值个数
for j=1 to 变量个数
找到Alternatives中第j列的位置L(i,j),命名为A
for k=−Re to Re
AF(A+k)j=Re1∗(Re−∣k∣) Fitness (i)+AF(A+k)j(4)
end
end
end
其中AF(A+k)j是为第j个变量选择的第(A+k)个可选值的累积适应度值(可选值的编号等于Alternatives矩阵的排序),Re为有效半径,在该半径内A的邻域的累积适应度都会受到A的适应度值的影响,该半径建议不超过搜索空间的1/4。
对于靠近边缘的可选值(A+k无效,A+k<0或A+k>LAj),AF将使用反射特征进行计算,这种情况下,如果可选值与边缘的距离小于Re,那么在边缘上放置一面镜子时,在上述可选值的镜像位置上存在相同的可选值。
(b)为了在搜索空间中更均匀地分布分布这种可能性,对所有的序列均加上一个很小的数AF=AF+ε,其中ε应该按照适应度值定义的方式选择,最好小于适应度值所能取得的最小值。
(c)找到当前循环中的最优位置,并记为最优位置“The best location”,找出分配给最优位置中各个变量的可选值,设置它们的AF为0,即:
for j=1 to 变量个数
for i=1 to 可选值个数
if i=The best location(j)
AFij=0
end
end
end
对于上述优化问题,首先根据等式(2)计算累积适应度值,前面提到过,可选值应该按照升序进行排列,则可选矩阵为:
-20 & -20 & -20 & -20 \\
-19 & -19 & -19 & -19 \\
\cdot & \cdot & \cdot & \cdot \\
\cdot & \cdot & \cdot & \cdot \\
\cdot & \cdot & \cdot & \cdot \\
19 & 19 & 19 & 19 \\
20 & 20 & 20 & 20
\end{array}\right]\tag{5}$$
对于采样位置$L_i$,考虑$R_e=10$,则等式(4)变为:
for $i=L_i$
 for $j$=1 to 4
  找到Alternatives中第$j$列的位置$L(i,j)$,命名为$A$
  for $k$=$-10$ to $10$
   $A F_{(A+k) j}=\frac{1}{10} *\left(10-|k|\right) \text { Fitness }(i)+A F_{(A+k) j}(6)$
  end
 end
end
其中式(5)也可表示为:
for $j={1,2,3,4}$
 $L(i,j)={-10,4,-7,18}$,那么$A={11,25,14,39}$,-10在可选值矩阵的第一列中排在第11位,以此类推就可以得到$A$。
 for $k$=-10 to 10
  $A F_{(11+k) 1}=\frac{1}{10} *\left(10-|k|\right) \text { Fitness }(i)+A F_{(11+k) 1}(7)$
  $A F_{(25+k) 2}=\frac{1}{10} *\left(10-|k|\right) \text { Fitness }(i)+A F_{(25+k) 2}$
  $A F_{(14+k) 3}=\frac{1}{10} *\left(10-|k|\right) \text { Fitness }(i)+A F_{(14+k) 3}$
  $A F_{(39+k) 4}=\frac{1}{10} *\left(10-|k|\right) \text { Fitness }(i)+A F_{(39+k) 4}$
 end
end
$\epsilon=1/(4*20^2)$,那么$AF=AF+0.000625$。
在式(7)的这些等式中,对于第2个变量$j=2$,在计算累积适应度时,应该将搜索空间分为两个区域:受影响区域(有效半径内)和不受影响区域。设定$R_e=10$,由于第2个变量选择的可选值为4,那么与4的距离大于10($x<6$或$x>10$)的区域不会受到影响。同时在受影响的区域内,由该样本位置产生的累积适应度线性变化,其最大值出现在x=4处,则有:
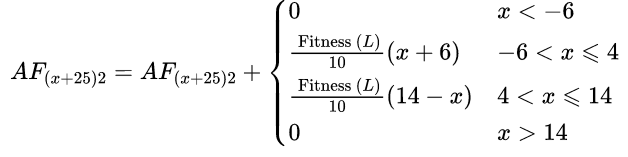
$AF=AF+0.000625$
对所有随机选择的解进行以上操作,就得到了第一次循环的最终累积适应度。
5. 对于变量$j_{(j=1 to NV)}$,根据以下关系计算选择可选值$i_{(i=1toAL_j)}$的概率:
$$P_{i j}=\frac{A F_{i j}}{\sum_{i=1}^{L A j} A F_{i j}}\tag{8}$$
根据分配给每个可选值的概率,计算下一步的位置。
在该例中,对于变量$j_{(j=1 to 4)}$,计算可选值$i_{(i=1to40)}$的概率:
$$P_{i j}=\frac{A F_{i j}}{\sum_{k=1}^{40} A F_{k j}}\tag{9}$$
6. 为最优位置的所有变量选择的所有可选值分配概率$PP$,根据下面的公式,把其余的概率分配给其他可选值:
for $j=1$ to 变量个数
 for $i=1$ to 可选值个数
  if $i=1$ The best location($j$)
   $P_{ij}=PP$ (10)
  else
   $P_{ij}=(1-PP)P_{ij}$ (11)
  end
 end
end
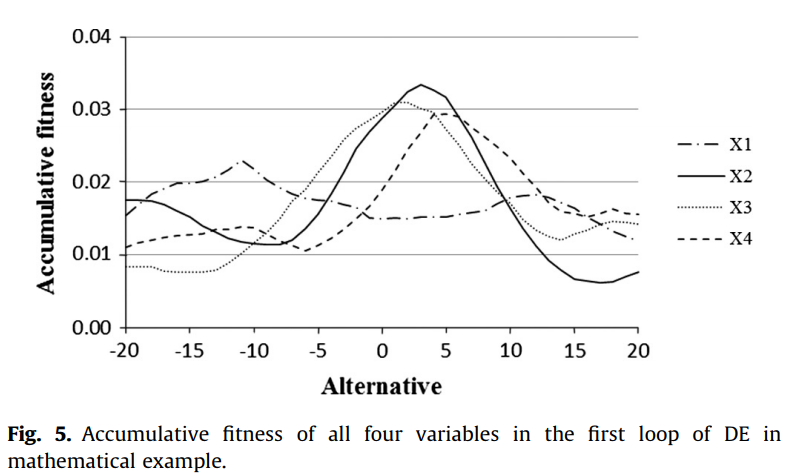
第一次循环的最优位置为$X1=-11,X2=3,X3=X4=4$,根据等式(3),第一次循环的$PP=10\%$,即在最优位置上的所有变量的概率为$10\%$,而将剩余的$90\%$分配给其他可选值。
$$P_{i j}=(1-0.1) P_{i j}=0.9 P_{i j}\tag{12}$$