激活函数通过引入非线性在神经网络中发挥了不可或缺的作用。这种非线性使得神经网络能够根据输入开发出复杂的表征和功能,而这在简单的线性回归模型中是不可能的。
在神经网络的历史上,已经有许多不同的非线性激活函数被提出。在这篇文章中,我们将探讨三个流行的函数:sigmoid, tanh, 和ReLU。
读完这篇文章后,你将了解到。
- 为什么非线性在神经网络中很重要?
- 不同的激活函数如何有助于解决梯度消失的问题
- Sigmoid、tanh和ReLU激活函数
- 如何在你的TensorFlow模型中使用不同的激活函数
概述
本文分为五个部分,它们是:
- 为什么我们需要非线性激活函数
- Sigmoid函数和梯度消失
- 双曲切线函数
- 矫正线性单元(ReLU)
- 在实践中使用激活函数
为什么我们需要非线性激活函数
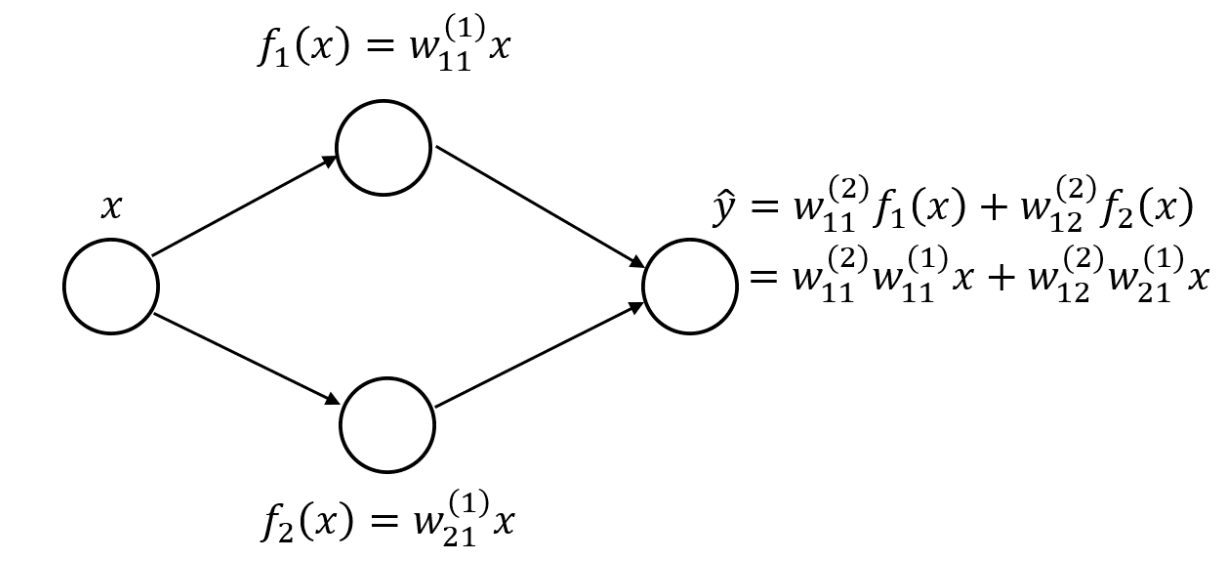
你可能想知道,为什么要大肆宣传非线性激活函数?或者说,为什么我们不能在上一层激活的加权线性组合之后使用一个身份函数。使用多个线性层基本上与使用单个线性层是一样的。这可以通过一个简单的例子来看。假设我们有一个单隐层的神经网络,每层有两个隐藏的神经元。
带有线性层的单隐层神经网络
然后我们可以将输出层改写为原始输入变量的线性组合,如果我们使用线性隐藏层的话。如果我们有更多的神经元和权重,那么这个方程会更长,有更多的嵌套和连续层权重之间的乘法,但想法仍然是一样的:我们可以把整个网络表示为一个单一的线性层。为了使网络能够表示更复杂的功能,我们需要非线性激活函数。让我们从一个流行的例子开始,即sigmoid函数。
西格玛函数和消失的梯度
对于神经网络的非线性激活函数,sigmoid激活函数是一个流行的选择。它受欢迎的一个原因是它的输出值在0和1之间,模仿了概率值,因此被用来将线性层的实值输出转换为概率,可以作为概率输出使用。这也使得它成为逻辑回归方法的一个重要组成部分,可以直接用于二元分类。
sigmoid函数通常用表示,其形式为。在TensorFlow中,我们可以从Keras库中调用sigmoid函数,如下所示。
import tensorflow as tf
from tensorflow.keras.activations import sigmoid
input_array = tf.constant([-1, 0, 1], dtype=tf.float32)
print (sigmoid(input_array))
这样我们就可以得到输出。
tf.Tensor([0.26894143 0.5 0.7310586 ], shape=(3,), dtype=float32)
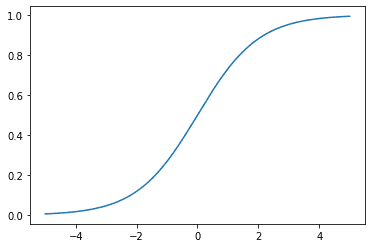
我们也可以将sigmoid函数作为的函数来绘制。
Sigmoid激活函数
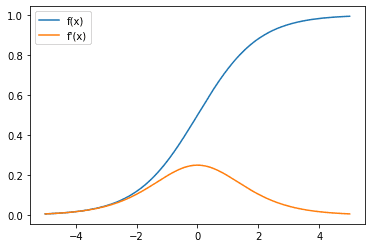
在观察神经网络中神经元的激活函数时,由于反向传播和链式规则会影响神经网络如何从数据中学习,我们也应该对其导数感兴趣。
Sigmoid激活函数(蓝色)和梯度(橙色)
在这里,我们可以观察到,sigmoid函数的梯度总是在0和0.25之间。当趋向于正或负无穷大时,梯度趋向于零。这可能导致梯度消失的问题,当输入在的某个大的量级时(例如,由于早期层的输出),梯度太小,无法启动校正。
梯度消失是一个问题,因为我们在深度神经网络的反向传播中使用了连锁规则。回顾一下,在神经网络中,每一层的梯度(损失函数)是其后续层的梯度乘以其激活函数的梯度。由于网络中有很多层,如果激活函数的梯度小于1,那么离输出较远的某一层的梯度将接近于零。而任何一层的梯度接近于零,就会阻止梯度进一步向前面的层传播。
由于sigmoid函数总是小于1,一个有更多层的网络会加剧梯度消失的问题。此外,存在一个饱和区域,即sigmoid函数的梯度趋于0,也就是的幅度较大的地方。因此,如果前几层激活的加权和的输出很大,那么我们将有一个非常小的梯度通过这个神经元传播,因为激活相对于激活函数输入的导数将很小(在饱和区域)。
当然,还有相对于前一层激活的线性项的导数,这对该层来说可能大于1,因为权重可能很大,而且它是不同神经元的导数之和。然而,由于权重通常被初始化为小值,在训练开始时,它仍然可能引起关注。
双曲正切函数
我们可以考虑的另一个激活函数是tanh激活函数,也被称为双曲正切函数。与sigmoid函数相比,它的输出值范围更大,而且最大梯度也更大。tanh函数是大多数人熟悉的圆的正切函数的双曲类似物。
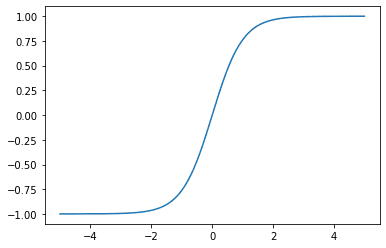
绘制出tanh函数。
tanh激活函数
我们也来看看梯度的情况。
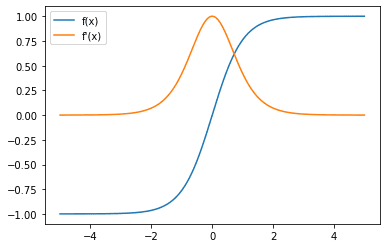
Tanh激活函数(蓝色)和梯度(橙色)。
注意,现在梯度的最大值是1,而sigmoid函数的最大梯度值是0。然而,tanh函数也有一个饱和区域,当输入的大小变大时,梯度值会趋向于饱和。
在TensorFlow中,我们可以使用Keras的激活模块中的tanh 函数在张量上实现tanh激活。
import tensorflow as tf
from tensorflow.keras.activations import tanh
input_array = tf.constant([-1, 0, 1], dtype=tf.float32)
print (tanh(input_array))
它的输出是
tf.Tensor([-0.7615942 0. 0.7615942], shape=(3,), dtype=float32)
矫正线性单元(ReLU)
我们要详细研究的最后一个激活函数是整流线性单元,也被普遍称为ReLU。它最近变得很流行,因为它的计算相对简单,有助于加快神经网络的速度,而且似乎得到了经验上的良好表现,这使它成为激活函数的一个很好的起始选择。
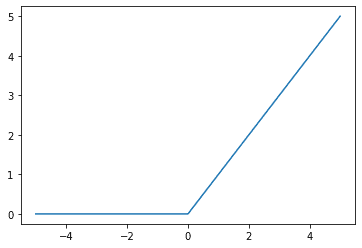
ReLU函数是一个简单的函数,它也可以被认为是一个分片函数,所有小于0的输入都映射到0,所有大于或等于0的输入都映射回自己(即,身份函数)。图形化。
ReLU激活函数
接下来,我们还可以看一下ReLU函数的梯度。
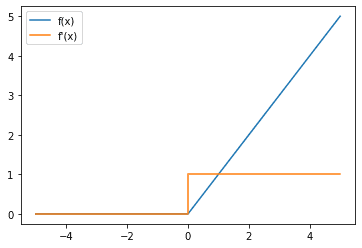
ReLU激活函数(蓝线)和梯度(橙色)
注意,只要输入是正的,ReLU的梯度就是1,这对解决梯度消失的问题很有帮助。然而,每当输入为负数时,梯度为0,这可能会导致另一个问题,即死神经元/垂死的ReLU问题,如果一个神经元持续失活,这就是一个问题。在这种情况下,神经元永远无法学习,其权重也不会因为链式规则而被更新,因为它的梯度是0,是它的一个项。如果这种情况发生在你的数据集中的所有数据上,那么这个神经元就很难从你的数据集中学习,除非前一层的激活发生变化,使神经元不再 "死亡"。
要在TensorFlow中使用ReLU激活。
import tensorflow as tf
from tensorflow.keras.activations import relu
input_array = tf.constant([-1, 0, 1], dtype=tf.float32)
print (relu(input_array))
这就给了我们输出。
tf.Tensor([0. 0. 1.], shape=(3,), dtype=float32)
在我们上面回顾的三个激活函数中,我们看到它们都是单调增加的函数。这是必须的,否则我们无法应用梯度下降算法。
现在我们已经探讨了一些常见的激活函数以及如何在TensorFlow中使用它们,让我们来看看如何在实际模型中使用这些函数。
在实践中使用激活函数
在我们探索激活函数在实践中的使用之前,让我们看看另一种常见的方式,当激活函数与另一个Keras层结合时,我们可以使用它们。比方说,我们想在Dense层上面添加一个ReLU激活功能。按照上面显示的方法,我们可以做到的一种方式是做
x = Dense(units=10)(input_layer)
x = relu(x)
然而,对于许多Keras层,我们也可以使用一个更紧凑的表示法来在层的顶部添加激活。
x = Dense(units=10, activation=”relu”)(input_layer)
使用这种更紧凑的表示法,让我们用Keras建立我们的LeNet5模型。
import tensorflow as tf
import tensorflow.keras as keras
from tensorflow.keras.layers import Dense, Input, Flatten, Conv2D, BatchNormalization, MaxPool2D
from tensorflow.keras.models import Model
(trainX, trainY), (testX, testY) = keras.datasets.cifar10.load_data()
input_layer = Input(shape=(32,32,3,))
x = Conv2D(filters=6, kernel_size=(5,5), padding="same", activation="relu")(input_layer)
x = MaxPool2D(pool_size=(2,2))(x)
x = Conv2D(filters=16, kernel_size=(5,5), padding="same", activation="relu")(x)
x = MaxPool2D(pool_size=(2, 2))(x)
x = Conv2D(filters=120, kernel_size=(5,5), padding="same", activation="relu")(x)
x = Flatten()(x)
x = Dense(units=84, activation="relu")(x)
x = Dense(units=10, activation="softmax")(x)
model = Model(inputs=input_layer, outputs=x)
print(model.summary())
model.compile(optimizer="adam", loss=tf.keras.losses.SparseCategoricalCrossentropy(), metrics="acc")
history = model.fit(x=trainX, y=trainY, batch_size=256, epochs=10, validation_data=(testX, testY))
而运行这段代码,我们可以得到输出结果
Model: "model"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) [(None, 32, 32, 3)] 0
conv2d (Conv2D) (None, 32, 32, 6) 456
max_pooling2d (MaxPooling2D (None, 16, 16, 6) 0
)
conv2d_1 (Conv2D) (None, 16, 16, 16) 2416
max_pooling2d_1 (MaxPooling (None, 8, 8, 16) 0
2D)
conv2d_2 (Conv2D) (None, 8, 8, 120) 48120
flatten (Flatten) (None, 7680) 0
dense (Dense) (None, 84) 645204
dense_1 (Dense) (None, 10) 850
=================================================================
Total params: 697,046
Trainable params: 697,046
Non-trainable params: 0
_________________________________________________________________
None
Epoch 1/10
196/196 [==============================] - 14s 11ms/step - loss: 2.9758 acc: 0.3390 - val_loss: 1.5530 - val_acc: 0.4513
Epoch 2/10
196/196 [==============================] - 2s 8ms/step - loss: 1.4319 - acc: 0.4927 - val_loss: 1.3814 - val_acc: 0.5106
Epoch 3/10
196/196 [==============================] - 2s 8ms/step - loss: 1.2505 - acc: 0.5583 - val_loss: 1.3595 - val_acc: 0.5170
Epoch 4/10
196/196 [==============================] - 2s 8ms/step - loss: 1.1127 - acc: 0.6094 - val_loss: 1.2892 - val_acc: 0.5534
Epoch 5/10
196/196 [==============================] - 2s 8ms/step - loss: 0.9763 - acc: 0.6594 - val_loss: 1.3228 - val_acc: 0.5513
Epoch 6/10
196/196 [==============================] - 2s 8ms/step - loss: 0.8510 - acc: 0.7017 - val_loss: 1.3953 - val_acc: 0.5494
Epoch 7/10
196/196 [==============================] - 2s 8ms/step - loss: 0.7361 - acc: 0.7426 - val_loss: 1.4123 - val_acc: 0.5488
Epoch 8/10
196/196 [==============================] - 2s 8ms/step - loss: 0.6060 - acc: 0.7894 - val_loss: 1.5356 - val_acc: 0.5435
Epoch 9/10
196/196 [==============================] - 2s 8ms/step - loss: 0.5020 - acc: 0.8265 - val_loss: 1.7801 - val_acc: 0.5333
Epoch 10/10
196/196 [==============================] - 2s 8ms/step - loss: 0.4013 - acc: 0.8605 - val_loss: 1.8308 - val_acc: 0.5417
这就是我们如何在我们的TensorFlow模型中使用不同的激活函数!
总结
在这篇文章中,你已经看到了为什么激活函数对于我们今天看到的深度学习中常见的复杂的神经网络是很重要的。你还看到了一些流行的激活函数,它们的导数,以及如何将它们整合到你的TensorFlow模型中。
具体来说,你学到了:
- 为什么非线性在神经网络中是很重要的
- 不同的激活函数如何有助于解决梯度消失的问题
- Sigmoid, tanh, 和ReLU激活函数
- 如何在你的TensorFlow模型中使用不同的激活函数