学习TensorFlow中的损失函数

损失指标对神经网络非常重要。由于所有的机器学习模型都是一个优化问题，损失是要最小化的目标函数。在神经网络中，优化是通过梯度下降和反向传播完成的。但什么是损失函数，它们是如何影响我们的神经网络的？

在这篇文章中，我们将介绍什么是损失函数，并深入探讨一些常用的损失函数，以及你如何将它们应用到你的神经网络。

读完这篇文章后，你将学会。

• 什么是损失函数，它们与度量有什么不同
• 用于回归和分类问题的常见损失函数
• 如何在你的TensorFlow模型中使用损失函数

让我们开始吧!

概述

本文分为五个部分，它们是

• 什么是损失函数？
• 平均绝对误差
• 平均平方误差
• 分类交叉熵
• 实践中的损失函数

什么是损失函数？

在神经网络中，损失函数有助于优化模型的性能。它们通常被用来衡量模型在其预测中所产生的一些惩罚，例如预测与地面真实标签的偏差。损失函数通常在其领域内是可微分的（但允许梯度只在非常具体的点上是未定义的，如x=0，这在实践中基本上被忽略）。在训练循环中，我们根据参数对它们进行微分，并将这些梯度用于我们的反向传播和梯度下降步骤，以优化我们在训练集上的模型。

损失函数也与度量略有不同。虽然损失函数可以告诉我们模型的性能，但它们可能不是人类直接感兴趣或容易解释的。这就是度量的作用。准确度等指标对于人类理解神经网络的性能更加有用，尽管它们可能不是损失函数的好选择，因为它们可能不是可微分的。

在下文中，让我们探讨一些常见的损失函数，特别是平均绝对误差、平均平方误差和分类交叉熵。

平均绝对误差

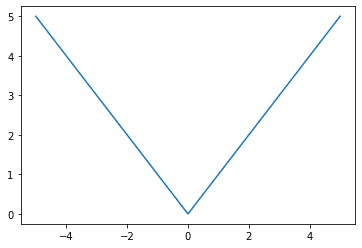
平均绝对误差（MAE）测量预测值和地面真实标签之间的绝对差异，并取所有训练实例中差异的平均值。在数学上，它等于$frac{1}{m}\\sum\_{i=1}^m\\lvert\\hat{y}\_i-y\_i\\rvert$，其中$m$是训练实例的数量，$y\_i$和$hat{y}\_i$分别是地面真实和预测值，我们在所有训练实例中取平均值。MAE从不为负，但只有在预测值与地面实况完全吻合时才为零。它是一个直观的损失函数，也可以作为我们的衡量标准之一，特别是对于回归问题，因为我们想使预测的误差最小。

让我们来看看平均绝对误差损失函数的图形是什么样的。

平均绝对误差损失函数，x=0处的地面真相和x轴代表预测值

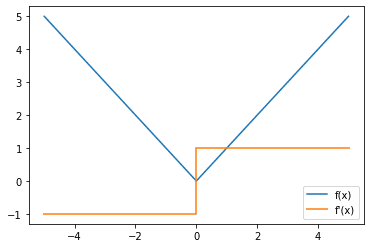
与激活函数类似，我们通常也对损失函数的梯度感兴趣，因为我们以后要用梯度来做反向传播来训练我们模型的参数。

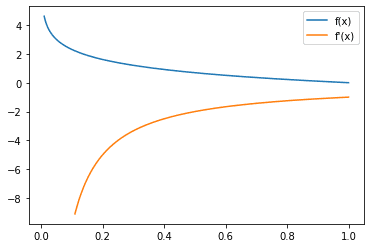
平均绝对误差损失函数（蓝色）和梯度（橙色）

我们注意到在平均绝对损失函数的梯度函数中有一个不连续点，但我们倾向于忽略它，因为它只发生在x=0处，而实际上很少发生，因为它是一个连续分布中单点的概率。

让我们来看看如何在TensorFlow中使用Keras损失模块来实现这个损失函数。

import tensorflow as tf
from tensorflow.keras.losses import MeanAbsoluteError

y_true = [1., 0.]
y_pred = [2., 3.]

mae_loss = MeanAbsoluteError()

print(mae_loss(y_true, y_pred).numpy())

这让我们如愿以偿地得到了2.0 ，因为$\\frac{1}{2}(\\lvert 2-1\\rvert + \\lvert 3-0\\rvert) = \\frac{1}{2}(4) = 4$。接下来，让我们来探讨另一个回归模型的损失函数，其属性略有不同，即平均平方误差。

平均平方误差

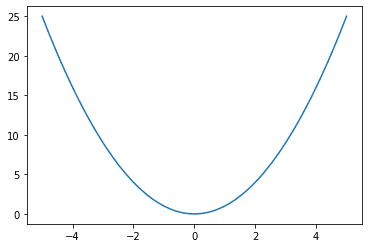
另一个流行的回归模型损失函数是平均平方误差（MSE），它等于$frac{1}{m}\\sum\_{i=1}^m（\\hat{y}\_i-y\_i）^2$。它与平均绝对误差相似，因为它也衡量预测值与地面真实值的偏差。然而，平均平方误差是对这一差异的平方（总是非负的，因为实数的平方总是非负的），这使得它的属性略有不同。

一个值得注意的是，平均平方误差有利于大量的小误差，而不是少量的大误差，这导致模型的离群值较少，或者至少离群值比用平均绝对误差训练的模型要小。这是因为与小误差相比，大误差对误差的影响要大得多，从而对误差的梯度也有影响。

图示。

平均平方误差损失函数，x=0处的地面真相和x轴代表预测值

然后，看一下梯度。

平均平方误差损失函数（蓝色）和梯度（橙色）。

请注意，更大的误差会导致梯度更大的幅度，也会导致更大的损失。因此，举例来说，两个偏离其基础真理1个单位的训练实例将导致2的损失，而一个偏离其基础真理2个单位的训练实例将导致4的损失，因此影响更大。

让我们来看看如何在TensorFlow中实现平均平方损失。

import tensorflow as tf
from tensorflow.keras.losses import MeanSquaredError

y_true = [1., 0.]
y_pred = [2., 3.]

mse_loss = MeanSquaredError()

print(mse_loss(y_true, y_pred).numpy())

它的输出5.0 ，因为frac{1}{2}\[(2-1)^2 + (3-0)^2\] = frac{1}{2}(10) = 5。请注意，第二个例子的预测值为3，实际值为0，在平均平方误差下贡献了90%的误差，在平均绝对误差下贡献了75%的误差。

有时，你可能会看到有人用均方根误差（RMSE）作为衡量标准。这是取MSE的平方根。从损失函数的角度来看，MSE和RMSE是等同的。

MAE和MSE都是在一个连续的范围内测量数值。因此，它们是针对回归问题的。对于分类问题，我们可以使用分类交叉熵。

分类交叉熵

前面两个损失函数是针对回归模型的，其中输出可能是任何实数。然而，对于分类问题，有一个小的、离散的数字集，输出可以采取。此外，我们用来标记编码类的数字是任意的，没有任何语义（例如，如果我们用0表示猫，1表示狗，2表示马，这并不代表狗是一半的猫和一半的马）。因此，它不应该对模型的性能产生影响。

在一个分类问题中，模型的输出是每个类别的概率向量。在Keras模型中，通常我们希望这个向量是 "logits"，即使用softmax函数将实数转换为概率，或者是softmax激活函数的输出。

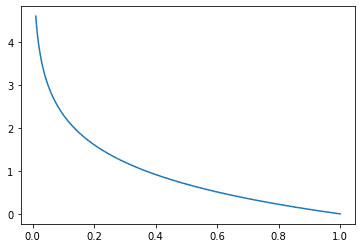
两个概率分布之间的交叉熵是对两个概率分布之间差异的衡量。准确地说，它是$-sum\_i P(X = x\_i) \\log Q(X = x\_i)$的概率$P$和$Q$。在机器学习中，我们通常有训练数据提供的概率$P$和模型预测的概率$Q$，其中$P$对于正确的类是1，对于其他每一个类是0。然而，预测的概率$Q$通常在0和1之间。因此，当用于机器学习中的分类问题时，这个公式可以简化为。$$text{categorical cross entropy} = - \log p_{gt}$其中$p_{gt}$是模型对该特定样本的基础真实类的预测概率。

交叉熵指标有一个负号，因为当$x$趋于零时，$\\log(x)$趋于负无穷大。当概率接近0时，我们希望有较高的损失，而当概率接近1时，则希望有较低的损失。图形化。

分类交叉熵损失函数，其中x是地面真实类的预测概率

请注意，如果地面真实类的概率是1，那么损失正好是0。另外，当地面真相类的概率趋向于0时，损失也趋向于正无穷大，因此对不良预测有很大的惩罚。你可能会认识到这个损失函数的逻辑回归，它们是相似的，只是逻辑回归的损失是专门针对二元类的情况。

分类交叉熵损失函数（蓝色）和梯度（橙色）

现在，看一下交叉熵损失的梯度。

看一下梯度，我们可以看到梯度一般是负的，这也是意料之中的，因为要减少这个损失，我们会希望在地面真相类上的概率越高越好，记得梯度下降的方向和梯度相反。

在TensorFlow中，有两种不同的方法来实现分类交叉熵。第一种方法将单热向量作为输入。

import tensorflow as tf
from tensorflow.keras.losses import CategoricalCrossentropy

# using one hot vector representation
y_true = [[0, 1, 0], [1, 0, 0]]
y_pred = [[0.15, 0.75, 0.1], [0.75, 0.15, 0.1]]

cross_entropy_loss = CategoricalCrossentropy()

print(cross_entropy_loss(y_true, y_pred).numpy())

这给出的输出为0.2876821 ，如预期的那样，等于$-log(0.75)$。在TensorFlow中实现分类交叉熵损失的另一种方法是使用标签编码表示类，其中类是由一个非负整数表示的，而不是地面真相类。

import tensorflow as tf
from tensorflow.keras.losses import SparseCategoricalCrossentropy

y_true = [1, 0]
y_pred = [[0.15, 0.75, 0.1], [0.75, 0.15, 0.1]]

cross_entropy_loss = SparseCategoricalCrossentropy()

print(cross_entropy_loss(y_true, y_pred).numpy())

这也同样给出了输出0.2876821 。

现在我们已经探索了回归和分类模型的损失函数，让我们来看看我们如何在机器学习模型中使用损失函数。

损失函数的实践

让我们探讨一下如何在实践中使用损失函数。我们将通过MNIST数字分类数据集上的一个简单的密集模型来探讨这个问题。

首先，我们从Keras数据集模块下载数据。

import tensorflow.keras as keras

(trainX, trainY), (testX, testY) = keras.datasets.mnist.load_data()

然后，我们建立我们的模型。

from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense, Input, Flatten

model = Sequential([
          Input(shape=(28,28,1,)),
          Flatten(),
          Dense(units=84, activation="relu"),
          Dense(units=10, activation="softmax"),
      ])

print (model.summary())

然后我们看一下上述代码输出的模型架构。

_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 flatten_1 (Flatten)         (None, 784)               0         
                                                                 
 dense_2 (Dense)             (None, 84)                65940     
                                                                 
 dense_3 (Dense)             (None, 10)                850       
                                                                 
=================================================================
Total params: 66,790
Trainable params: 66,790
Non-trainable params: 0
_________________________________________________________________

然后我们可以编译我们的模型，这也是我们引入损失函数的地方。由于这是一个分类问题，我们将使用交叉熵损失。特别是，由于Keras数据集中的MNIST数据集是以标签而不是一热向量来表示的，所以我们将使用SparseCategoricalCrossEntropy损失。

model.compile(optimizer="adam", loss=tf.keras.losses.SparseCategoricalCrossentropy(), metrics="acc")

最后，我们训练我们的模型。

history = model.fit(x=trainX, y=trainY, batch_size=256, epochs=10, validation_data=(testX, testY))

我们的模型成功地进行了训练，输出结果如下。

Epoch 1/10
235/235 [==============================] - 2s 6ms/step - loss: 7.8607 - acc: 0.8184 - val_loss: 1.7445 - val_acc: 0.8789
Epoch 2/10
235/235 [==============================] - 1s 6ms/step - loss: 1.1011 - acc: 0.8854 - val_loss: 0.9082 - val_acc: 0.8821
Epoch 3/10
235/235 [==============================] - 1s 6ms/step - loss: 0.5729 - acc: 0.8998 - val_loss: 0.6689 - val_acc: 0.8927
Epoch 4/10
235/235 [==============================] - 1s 5ms/step - loss: 0.3911 - acc: 0.9203 - val_loss: 0.5406 - val_acc: 0.9097
Epoch 5/10
235/235 [==============================] - 1s 6ms/step - loss: 0.3016 - acc: 0.9306 - val_loss: 0.5024 - val_acc: 0.9182
Epoch 6/10
235/235 [==============================] - 1s 6ms/step - loss: 0.2443 - acc: 0.9405 - val_loss: 0.4571 - val_acc: 0.9242
Epoch 7/10
235/235 [==============================] - 1s 5ms/step - loss: 0.2076 - acc: 0.9469 - val_loss: 0.4173 - val_acc: 0.9282
Epoch 8/10
235/235 [==============================] - 1s 5ms/step - loss: 0.1852 - acc: 0.9514 - val_loss: 0.4335 - val_acc: 0.9287
Epoch 9/10
235/235 [==============================] - 1s 6ms/step - loss: 0.1576 - acc: 0.9577 - val_loss: 0.4217 - val_acc: 0.9342
Epoch 10/10
235/235 [==============================] - 1s 5ms/step - loss: 0.1455 - acc: 0.9597 - val_loss: 0.4151 - val_acc: 0.9344

这就是如何在TensorFlow模型中使用损失函数的一个例子。

结语

在这篇文章中，你已经看到了损失函数以及它们在神经网络中的作用。你还看到了回归和分类模型中使用的一些流行的损失函数，以及如何在TensorFlow模型中使用交叉熵损失函数。

具体来说，你学到了：

• 什么是损失函数，它们与度量有什么不同
• 回归和分类问题的常见损失函数
• 如何在你的TensorFlow模型中使用损失函数