0.论文信息和个人感言

  这篇论文是老师给推荐读的，在阅读之前我对于 Shapley 值进行了大概的了解，感觉还是很有意思的，但是论文实在看得半生不熟，很多细节都存疑，所以先做了简单大概的翻译放了上来，后续如果有更深入的理解会进行补充。

1.介绍

  Shapley 值是可解释人工智能中最受欢迎的模型不可知论方法之一。这些值旨在将模型预测和平均基线之间的差异归因于用作模型输入的不同要素。Shapley 值基于坚实的博弈论原理，唯一地满足几个理想的性质，这就是为什么它们越来越多地被用来解释可能复杂和高度非线性的机器学习模型的预测。当特征是独立的时，Shapley 值可以很好地根据用户的直觉进行校准，但当独立假设被违反时，可能会导致不受欢迎的、违反直觉的解释。

  在这篇文章中，作者提出了一个新的计算 Shapley 值的框架，该框架推广了最近旨在绕过独立性假设的工作。通过使用珀尔的DO演算，我们展示了如何在不牺牲任何期望的性质的情况下，为一般因果图导出这些“因果” Shapley 值。此外，因果 Shapley 值使我们能够区分直接和间接影响的贡献。我们给出了一个基于因果链图的计算因果 Shapley 值的实用实现，并在一个真实世界的例子中说明了它们的实用性。

2.因果 Shapley 值

  我们假设给我们一个机器学习模型 $f(\cdot)$，它可以为任何特征向量 x 生成预测。我们的目标是为单个预测 $f(x)$ 提供解释，它考虑了现实世界中特征之间的因果关系。

  归因方法以 Shapley 值为最突出的例子，通过将 $f(x)$ 与基线 $f_0$ 之间的差异归因于 $i\in N,N=\{1,2,...,n\}$ 的不同特征，来提供对单个预测的局部解释 :

  其中 $\phi_i$ 是特征 i 对预测 $f(x)$ 的贡献。对于基线 $f_0$，我们将取平均预测值 $f_0=\mathbb{E}f(X)$，并取观测数据分布 $P(X)$ 的期望值。方程式 (1) 被称为效率性质，这似乎是任何归因方法的合理要求，因此我们以此作为起点。

  为了从不知道 $f_0$ 的任何特征值到知道所有的特征值，对于 $f(x)$，我们可以一个接一个地添加特征值，以特定的顺序 $\pi$ 主动地将特征设置为它们的值。我们将给定置换 $\pi$ 的特征 i 的贡献定义为将特征设置为其值之前和之后的值函数的差：

  对于 $j\prec_\pi i$，如果 j 在排列 $\pi$ 中在 i 之前，并且我们选择值函数

  这里，S 是具有已知特征值 $x_S$ 的联合索引的子集。为了计算期望值，我们令 $\bar{S}=N\setminus S$ (S的补码) 对“联盟外”或丢弃的特征 $\mathbf{X}_{\bar{S}}$ 进行平均。为了明确地考虑到“联盟内”特征和“联盟外”特征之间可能的因果关系，我们建议采用 Pearl 的 do 运算来满足‘通过干预’的条件。换言之，贡献 $\phi_i(\pi)$ 现在通过 (平均) 预测来衡量特征 i 的相关性，如果我们主动将特征 i 设置为其值与未知其值的 (的反事实情况) 相比获得的 (平均) 预测。

  由于式子 (2) 中的特征 i 之和是伸缩的，所以效率性质 (1) 对任何排列 $\pi$ 都成立。因此，对于排列 $w(\pi)$ 上的任意分布且 $\sum_\pi w(\pi)=1$

  仍然满足 (1)。一个明显的选择是采用均匀分布 $w(\pi)=1/n!$。然后我们得出 (单件 $\{i\}$ 的速记为 i) :

  除了效率，Shapley 值还唯一地满足其他三个所需的性质。

线性性质 : $\phi_i(\alpha_1v_1+\alpha_2v_2)=\alpha_1\phi_i(v_1)+\alpha_2\phi_i(v_2)$

空值附加 : 如果对于所有的 $S\subseteq N\setminus i$ 有 $v(S\cup i)=v(S)$，则有 $\phi_i=0$

对称性质 : 如果 $v(S\cup i)=v(S\cup j)$ 对所有 $S\subseteq\{i,j\}$，则 $\phi_i=\phi_j$.这种意义上的对称性同样适用于边际、条件和因果 Shapley 值。

  请注意，这里的对称性定义为 w.r.t。对于贡献 $\phi_i$，而不是函数值f(X)。正如在 [8] 中第3节中所讨论的那样，通过观察或干预来限制条件不会破坏对称性。对于排列的非均匀分布，如[6]，对称性丢失，但效率、线性和零玩家仍然适用。

  到目前为止，我们对 Shapley 值的积极介入解释与文献 [3，8，17] 中的解释一致。然而，从现在开始，Janzing等人 [8] 通过正式区分真实要素 (对应于其中一个数据点) 和作为输入插入到模型中的要素，选择忽略真实世界中要素之间的任何依赖关系。由此得出的结论是，在我们的记法中，对于任何子集 S，$P(\mathbf{X}_{\bar{S}}|\text{do}(\mathbf{X}))=P(\mathbf{X}_{\bar{S}})$。因此，在干预条件下的任何期望都塌缩为边际期望，并且在 [3，8，17] 的解释中，干预 Shapley 值简化为边际 Shapley 值。正如我们将在下面看到的，边际 Shapley 值只能代表直接影响，这使得具有强烈间接影响 (例如遗传标记) 的“根本原因”在归因中被忽略，这与人类倾向于归因于原因的方式截然不同 [29]。在本文中，我们选择不对真实世界的特征和预测模型的输入进行这种区分，而是显式地考虑现实世界中数据之间的因果关系，以加强解释。由于术语“介入” Shapley 值是用来对预测算法进行因果解释的，忽略了真实世界中特征之间的因果关系，所以我们将使用术语“因果” Shapley 值来表示那些确实试图使用珀尔的 $\text{do}$-演算纳入这些关系的计算值。

  在 [6] 中介绍的非对称 Shapley 值 (另见这些论文集) 具有相同的目标：通过结合关于真实世界中特征的因果知识来增强对 Shapley 值的解释。在 [6] 中，通过选择 (4) 中的 $w(\pi)\ne0$，仅对于那些与特征之间的因果结构一致的排列 $\pi$，即使得已知的因果祖先总是在其后代之前，结合了这一知识。最重要的是，Frey 等人 [6] 通过观察应用标准条件。在这篇文章中，我们证明了没有必要求助于不对称的 Shapley 值来结合因果知识：通过干预来应用条件作用而不是通过观察来条件作用就足够了。选择不对称的 Shapley 值而不是对称的 Shapley 值可以被认为与通过观察选择条件反射与通过干预选择条件反射是正交的。因此，我们将把 [6] 的方法称为非对称条件 Shapley 值，以将它们与实现这两种思想的非对称因果 Shapley 值进行对比。

3.将因果 Shapley 值分解为直接和间接

  我们的因果解释使我们能够区分每个特征对模型预测的直接和间接影响。这种分解还有助于理解边际 Shapley 值、对称 Shapley 值和非对称 Shapley 值之间的差异。返回到 (2) 中的排序 $\pi$ 和特征 i 的贡献 $\phi_i(\pi)$，并使用速记 $\underline{S}=\left\{j:j\prec_\pi i\right\}$ 和 $\bar{S}=\left\{j:j\succ_\pi i\right\}$，我们可以将该置换的总效应分解为直接和间接效应：

  当随机特征 $X_i$ 被其特征值 $x_i$ 替换时，直接影响测量预测中的预期变化，而不改变其他联盟外特征的分布。间接效应衡量了由于额外干预 $\text{do}(X_i=x_i)$ 而导致其他联盟外特征的分布发生变化时预期的差异。然后，Shapley 值的直接和间接部分可以像式子 (4) 中那样计算：通过对所有排列取一个可能加权的平均值。条件 Shapley 值可以通过在 (5) 中用观察条件代替干预条件来类似地分解。对于边际 Shapley 值，没有条件，因此没有间接影响：通过构造，边际 Shapley 值只能代表直接影响。我们将在下一节中利用这种分解来阐明不同的因果结构如何导致不同的 Shapley 值。

4.不同因果架构的 Shapley 值

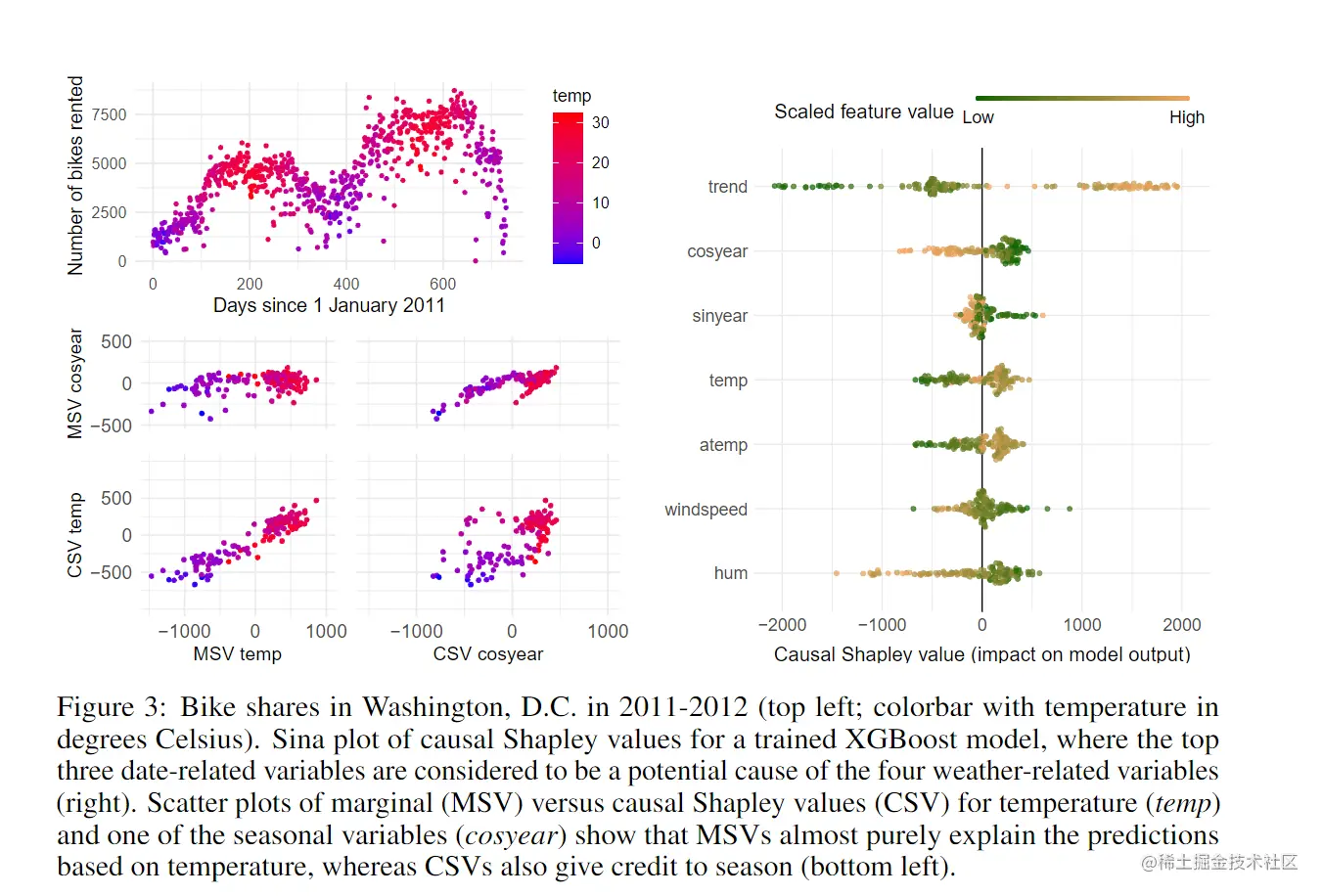
  为了说明不同 Shapley 值之间的差异，我们考虑了关于两个特征的四个因果模型。它们的构造使得它们具有相同的 P(X)，其中 $\mathbb{E}[X_2|x_1]=\alpha x_1$ 和 $\mathbb{E}[X_1]=\mathbb{E}[X_2]=0$，但对 $X_1$ 和 $X_2$ 之间的依赖关系具有不同的因果解释。例如，在因果链中，$X_1$ 可以表示季节、$X_2$ 温度和 $Y$ 自行车租赁。叉形结构中颠倒了 $X_1$ 和 $X_2$ 之间的箭头，现在 $Y$ 可能代表酒店入住率、$X_2$ 季节和 $X_1$ 温度。在链和叉结构中，不同的数据点对应不同的日子。对于混杂和循环，$X_1$ 和 $X_2$可能分别代表肥胖和睡眠呼吸暂停，以及 $Y$ 小时睡眠。混杂模型实现了这样的假设，即肥胖和睡眠呼吸暂停有一个共同的混杂因子$Z$，例如，一些遗传易感性。另一方面，这个循环代表了更常见的假设，即存在互惠效应，肥胖影响睡眠呼吸暂停，反之亦然 [22]。在混杂和循环中，不同的数据点对应不同的主题。我们假设已经训练了线性模型 $f(x_1,x_2)$，该线性模型恰好在很大程度上甚至完全简化了公式，忽略了第一个特征，并归结为预测函数 $f(x_1,x_2)=\beta x_2$。图1显示了在这种极端情况下，各种 Shapley 值为每个因果模型提供的解释。

  由于在所有情况下，$X_1$ 和预测之间没有直接联系，因此 $X_1$ 的直接影响总是等于零。同样，$X_2$ 的任何间接影响都只能通过 $X_1$，因此也必须等于零。因此，我们所能预期的是 $X_2$ 的直接影响，与 $\beta$ 成正比，以及 $X_1$ 到 $X_1$ 的间接影响，与 $\alpha$ 乘以 $\beta$ 成正比。由于充分性属性，直接和间接影响总是相加为输出 $\beta x_2$。这使得，对于所有不同的因果结构和 Shapley 值类型的组合，我们最终得到了三种不同的解释模式，在图1中称为 $D$、$E$ 和 $R$。

  为了论证哪些解释是有意义的，我们引用经典范数理论 [9]。它指出，当被要求解释一种影响时，人类会将实际观察结果与反事实的、更正常的替代方案进行对比。什么被认为是正常的，取决于背景。Shapley 值可以被给予相同的解释 [20] : 它们衡量知道和不知道特定特征的值之间的预测差异，其中对正态分布的选择转化为对参考分布的选择，以在特征值仍然未知的情况下对其进行平均。

  从这个角度来看，[3，8，17] 中的边际 Shapley 值对应于对什么是正常的非常简单、违反直觉的解释。例如，考虑链条的情况，$X_1$ 表示季节、$X_2$ 温度和 $Y$ 自行车租赁，以及温度同为为13摄氏度的两天，一天在秋天，另一天在冬天。对于这两天预测的自行车租赁量，边际 Shapley 值最终得到了相同的解释，忽略了冬季的气温高于一年中这个时候的正常水平，而秋季的气温低于正常水平。就像边际 Shapley 值一样，[1] 中的对称条件 Shapley 值不区分四种因果结构中的任何一种。它们确实考虑了两个特征之间的依赖关系，但随后没有承认对分叉和混杂中的特征 $X_1$ 的干预不会改变 $X_2$ 的分布。

  对于混杂和循环，不对称的 Shapley 值使 $X_1$ 和 $X_2$ 处于相同的地位，然后与它们的对称对应物重合。来自 [6] 的非对称条件 Shapley 值没有办法区分周期和混杂因素，在后一种情况下不切实际地将信用分配给 $X_1$。非对称和对称的因果 Shapley 值确实正确地处理了周期和混杂的情况。

  在链的情况下，不对称和对称的因果 Shapley 值提供了不同的解释。哪种解释更受欢迎，很可能取决于上下文。在我们的自行车租赁示例中，非对称 Shapley 值首先完全归功于季节的间接影响 (这里是 $\alpha\beta x_1$)，然后从温度的直接影响中减去这一点，以满足充分性属性 ($\beta x_2-\alpha\beta x_1$)。对称的因果 Shapley 值考虑了两种情况——一种是在温度之前干预季节，另一种是在季节之前干预温度——然后对这两种情况的结果进行平均。这种对称策略似乎更适合于追溯到 [14] 的理论，即人类通过对不同的可能场景 (这里：特征的不同顺序) 进行采样来判断因果关系。然而，在处理时间链事件时，另一种理论 (见[30]) 表明，人类倾向于将功劳或责任首先归因于根本原因，这似乎在精神上更接近不对称因果 Shapley 价值观提供的解释。

  通过放弃对称性，不对称的 Shapley 值确实付出了代价：它们对插入零强度的因果联系很敏感。例如，考虑训练成对两个二元变量 $X_1$和 $X_2$ 的 $\mathbf{XOR}$ 函数进行完美预测的神经网络。在所有特征上均匀分布，并且没有进一步的假设 w.r.t. 对于 $X_1$ 和 $X_2$ 的因果顺序，当预测 $f=1$ 时，Shapley 值为 $\phi_1=\phi2=\frac{1}{4}$；当 $f=0$：完全对称时，Shapley 值为 $\phi_1=\phi_2=−1/4$。如果我们现在假设 $X_1$ 先于 $X_2$ (并且因果强度为0以保持特征上的均匀分布)，则所有 Shapley 值保持不变，除了不对称的值：当 $f=1$ 时，这些值突然跳到 $\phi_1=0$ 和 $\phi_2=\frac{1}{2}$，而当 $f=0$ 时，$\phi_1=0$ 和 $\phi_2=-\frac{1}{2}$。关于这种不对称 Shapley 值的不稳定性的更多细节可以在附录中找到，在那里我们比较了不同因果强度的训练神经网络的 Shapley 值。

  总而言之，与边际和 (对称和非对称) 条件 Shapley 值不同，因果 Shapley 值提供了合理的解释，包含了现实世界中的因果关系。当因果关系源自明确的时间顺序时，非对称的因果关系 Shapley 值可能比对称的 Shapley 值更可取，而对称的 Shapley 值具有对模型错误规范的敏感性低得多的优势。

5.因果链图的一个实用实现

  在理想情况下，从业者可以获得一个完全指定的因果模型，该模型可以插入 (3) 以计算或采样感兴趣的每个干预概率。在实践中，这样的要求几乎不现实。事实上，即使从业者可以指定一个完整的因果结构 (包括潜在的混淆)，并且可以完全访问观察概率 $P(X)$，也不是每个因果查询都需要是可识别的 (例如，见 [24])。此外，要求如此多的先验知识可能不利于该方法的普遍适用性。在本节中，我们描述了一种实用的方法，当我们有权使用 (部分) 因果关系排序和一些额外信息来区分混杂因素和相互作用时，以及估计 $P(X)$ 的 (相关参数) 的训练集。我们的方法受到 [6] 的启发，但在各个方面进行了扩展：它提供了因果链图方面的形式化，适用于对称和非对称 Shapley 值，并正确区分了由于混淆和相互作用而产生的依赖关系。

  在可以给出特征的完全因果排序并且所有因果关系都没有混淆的特殊情况下，$P(X)$ 满足与有向无环图 (DAG) 相关联的马尔可夫性质，并且可以写成

  其中 $pa(j)$ 是节点 j 的亲本点。在没有进一步的条件独立性的情况下，j 的亲本点在因果顺序中都是在 j 之前的节点。对于因果DAG，我们有干预公式 [13]：

  对于 $pa(j)\cap T$，j 的亲本也是子集 T 的一部分。介入公式可用于回答感兴趣的任何因果问题。当我们不能给出单个变量之间的完全排序，但仍然是部分排序时，因果链图 [13] 就可以解决问题了。因果链图有有向边和无向边。在同等基础上处理的所有特征都通过无向边链接在一起，并成为同一链组件的一部分。链组件之间的边是有向的，表示因果关系。有关该过程的说明，请参见图2。链图中的概率分布 $P(X)$ 分解为 “链组件的DAG”：

  每个 $\tau$ 都是一个链组件，由平等对待的所有特征组成。

  如何计算干预的效果取决于对生成过程的解释，生成过程导致每个组件内特征之间的 (剩余) 依赖关系。如果我们假设这些是排挤掉一个常见混杂因素的结果，那么对特定功能的干预将打破与其他功能的依赖。我们将对其适用的链组分称为 $\mathcal{T}_{\text{confounding}}$。无向部分还可以对应于由组件内的变量之间的相互作用产生的动态过程的平衡分布[13]。在这种情况下，设置功能的值确实会影响变量在同一组件中的分布。我们将这些组件集合称为 $\mathcal{T}_{\overline{\text{confounding}}}$。

  计算因果 Shapley 值所需的任何干预预期都可以通过使用以下定理 (参见附录中更详细的证明和一些作为特例链接到其他类型 Shapley 值的推论)，通过观察转化为期望。

定理1.对于因果链图，我们得到了插入式公式

证明

  其中，每个等号上方的数字是指所应用的 [24] 中的标准 do 运算规则。对于具有由公共混杂引起的依赖关系的链组件，规则 (3) 再次适用并产生 $P(\mathbf{X}_{\tau\cap\bar{s}}|\mathbf{X}_{pa(\tau)\cap\bar{S}},x_{pa(\tau)\cap S})$，而对于具有相互作用引起的依赖关系的链组件，规则 (2) 再次适用并$P(\mathbf{X}_{\tau\cap\bar{s}}|\mathbf{X}_{pa(\tau)\cap\bar{S}},x_{pa(\tau)\cap S},x_{\tau\cap S})$。

  为了计算这些观测期望值，我们可以依靠已经提出的各种方法来计算条件 Shapley 值 [1，6]。在 [1] 之后，我们将假设 $P(X)$ 的多元高斯分布，这是我们从训练数据估计的。可供选择的建议包括假设高斯 Copula 分布、根据经验 (条件) 分布 (均来自[1]) 和变分自动编码器 [6] 进行估计。

6.真实世界数据的图解

略