与 泡沫排序一样,选择排序也是一种排序算法,特别是就地比较排序。选择排序算法的基础是找到未排序数组中的最小或最大元素或项目,然后将其放在排序数组中的正确位置。
C++中的选择排序
C++中的选择排序是一种简单明了的排序算法。选择排序算法是一种基于就地比较的算法,在这种算法中,列表或数组被分为两部分,最左端是已排序部分,最右端是未排序部分。因此,最初,排序部分是空的,而未排序部分是整个列表。
从未排序的数组中选择最小的元素,并与最左边的元素交换,该元素就成为已排序数组的一部分。这个过程继续将未排序数组的边界按分量向右移动。最后,我们得到排序后的值。综上所述。
选择排序算法将一个数组划分为 两个部分:
- 一个已排序的子数组
- 未排序的子数组,我们必须从其中挑选出最小的元素,然后将其放入已排序的数组中。
选择排序的算法。
选择(A,N)
第一步: 重复步骤2和3,为(k=0;k<n-1;k++)
第二步: 调用MINIMUM(A,K,N,LOC)
第三步: 交换A[K]和A[LOC]。
第四步: 退出
最小化(A,K,N,LOC)
第一步: 设置min=A[K]和LOC=K
第二步 重复步骤3和4 for(i=k;i<n;i++)
第三步: 如果min>a[i]
第四步: 设置min=a[i]和LOC=i
第五步 :返回LOC
用一个例子进行解释
从这个算法中,我们可以理解,如上所述,数组分为两部分,一部分是排序的,另一部分是未排序的。所以,我们从这个未排序的顺序中找到最小的值,然后把它放到一个排序顺序的列表中。
例如,让我们来看看一个整数的列表:
| 阵列编号 | 12 | 10 | 86 | 4 | 13 |
| 地点 | 0 | 1 | 2 | 3 | 4 |
第一遍
当K=0时, SELECTION() 将调用 MINIMUM() 并检查列表中最小的值,因此,在第一遍中,最低值是4, MINIMUM() 将返回4的位置,即 LOC=3。
然后, SELECTION() 将与当前A[0]=12的值交换。所以,交换值之后,新的数组将是:
| 数组编号 | 4 | 10 | 86 | 12 | 13 |
| 地点 | 0 | 1 | 2 | 3 | 4 |
第二遍
现在,K=1, SELECTION() 将 再次 调用 MINIMUM(), 然后它将检查未排序数组中最小的值10,然后它将返回10的位置,也就是LOC=1。
最终的数组将与10在其正确的位置相同。
第三遍
现在,K=2, SELECTION() 将 再次 调用 MINIMUM(), 然后它将检查未排序数组中最小的值,也就是12,然后它将返回12的位置,即 LOC=3。
然后, SELECTION() 将与当前A[2]=86的值交换。所以,交换值之后,新的数组将是:
| 数组编号 | 4 | 10 | 12 | 86 | 13 |
| 地点 | 0 | 1 | 2 | 3 | 4 |
第四遍
现在,K=3, SELECTION() 将 再次 调用 MINIMUM(), 然后它将检查未排序数组中最小的值,也就是13,然后它将返回13的位置,也就是 LOC=4。
然后, SELECTION() 将与当前A[3]=86的值交换。所以,交换值之后,新的数组将是:
| 数组编号 | 4 | 10 | 12 | 13 | 86 |
| 地点 | 0 | 1 | 2 | 3 | 4 |
选择排序伪代码
procedure selection sort
list : array of items
n : size of list
for i = 1 to n - 1
/* set current element as minimum*/
min = i
/* check the element to be minimum */
for j = i+1 to n
if list[j] < list[min] then
min = j;
end if
end for
/* swap the minimum element with the current element*/
if indexMin != i then
swap list[min] and list[i]
end if
end for
end procedure
选择排序的C++程序
请看下面selection.cpp的代码:
#include<bits/stdc++.h>
using namespace std;
int minimum(int a[],int n, int k, int loc)
{
loc=k;
int min=a[k];
for(int i=k;i<n;i++)
{
if(a[i]<min)
{
min=a[i];
loc=i;
}
}
return loc;
}
int selection(int a[],int n)
{
int loc=-1,k;
for(k=0;k<n-1;k++)
{
int loc1=minimum(a,n,k,loc);
int temp=a[k];
a[k]=a[loc1];
a[loc1]=temp;
}
cout<<"The sorted list is:\n";
for(k=0;k<n;k++)
cout<<a[k]<<" ";
}
int main()
{
int n;
cout<<"Enter the size of the array: ";
cin>>n;
int a[n],i;
cout<<"Enter the array values:\n";
for(i=0;i<n;i++)
{
cin>>a[i];
}
//calling selection function
selection(a,n);
return 0;
}
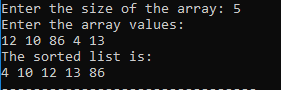
输出:
 时间复杂度:
时间复杂度:
如果我们想从N个元素的数组中找到最小的元素,需要进行N-1次比较。在将最小项放在适当的位置后,未排序数组的大小减少到N-1, 然后需要进行N-2次比较才能在未排序数组中找到最小项。
因此(N-1)+(N-2) +.......+1=(N⋅(N-1))/2次比较和N次交换,导致总体复杂度为O(N2)。
所以,选择排序的时间复杂度是O(n2),因为有两个嵌套循环。
辅助空间O(1)
选择排序的好处是,它永远不会进行超过O(n)次的交换,当内存写入是一个昂贵的操作时,它可以提供帮助。
本教程就到此为止。