用贝塞尔曲线画画(一)

携手创作，共同成长！这是我参与「掘金日新计划 · 8 月更文挑战」的第4天，点击查看活动详情

1. 什么是贝塞尔曲线

一句话解释：它可以将任何平滑曲线转化为精确的数学公式。例如PS中的钢笔工具，它的原理就是二阶贝塞尔曲线。

1.1. 一阶贝塞尔曲线

一阶贝塞尔曲线描述的是从p0到p1的连续点，是一条直线。公式如下：

$B(t)=(1-t)p_{0}+tp_{1},t\epsilon (0,1)$

写成下面这种形式，更好理解一点：

$B(t)=p_{0}+(p_{1}-p_{0})t,t\epsilon (0,1)$

其中$p_{0}$是起始点坐标，$p_{1}$是结束点坐标。

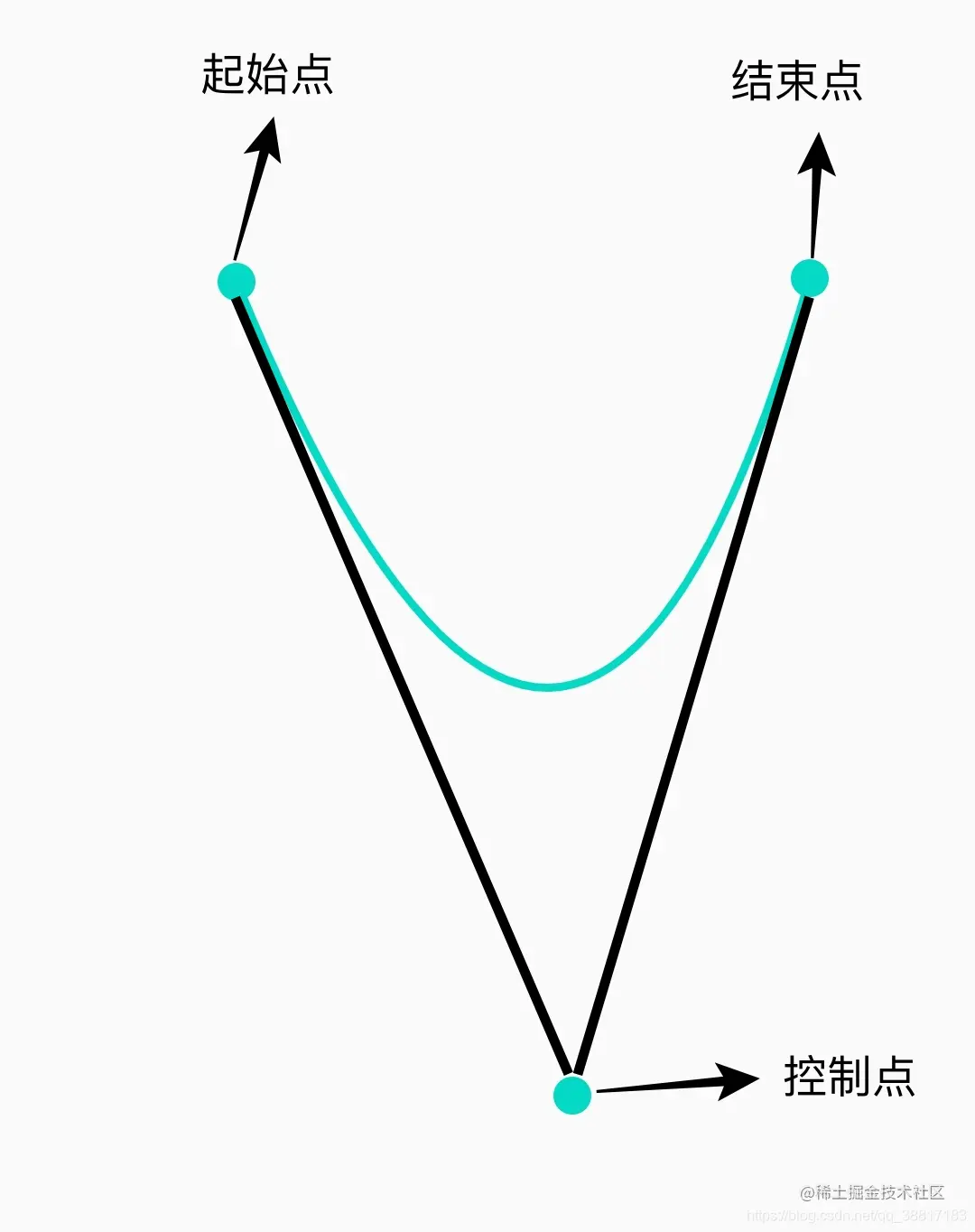
1.2. 二阶贝塞尔曲线

二阶贝塞尔曲线相对于一阶多了一个控制点，其公式为：

$B(t)=(1-t)^{2}p_{0}+2t(1-t)p_{1}+t^{2}p_{2},t\epsilon [0,1]$

其中$p_{0}$为起始点坐标，$p_{1}$为控制点，$p_{2}$为结束点。

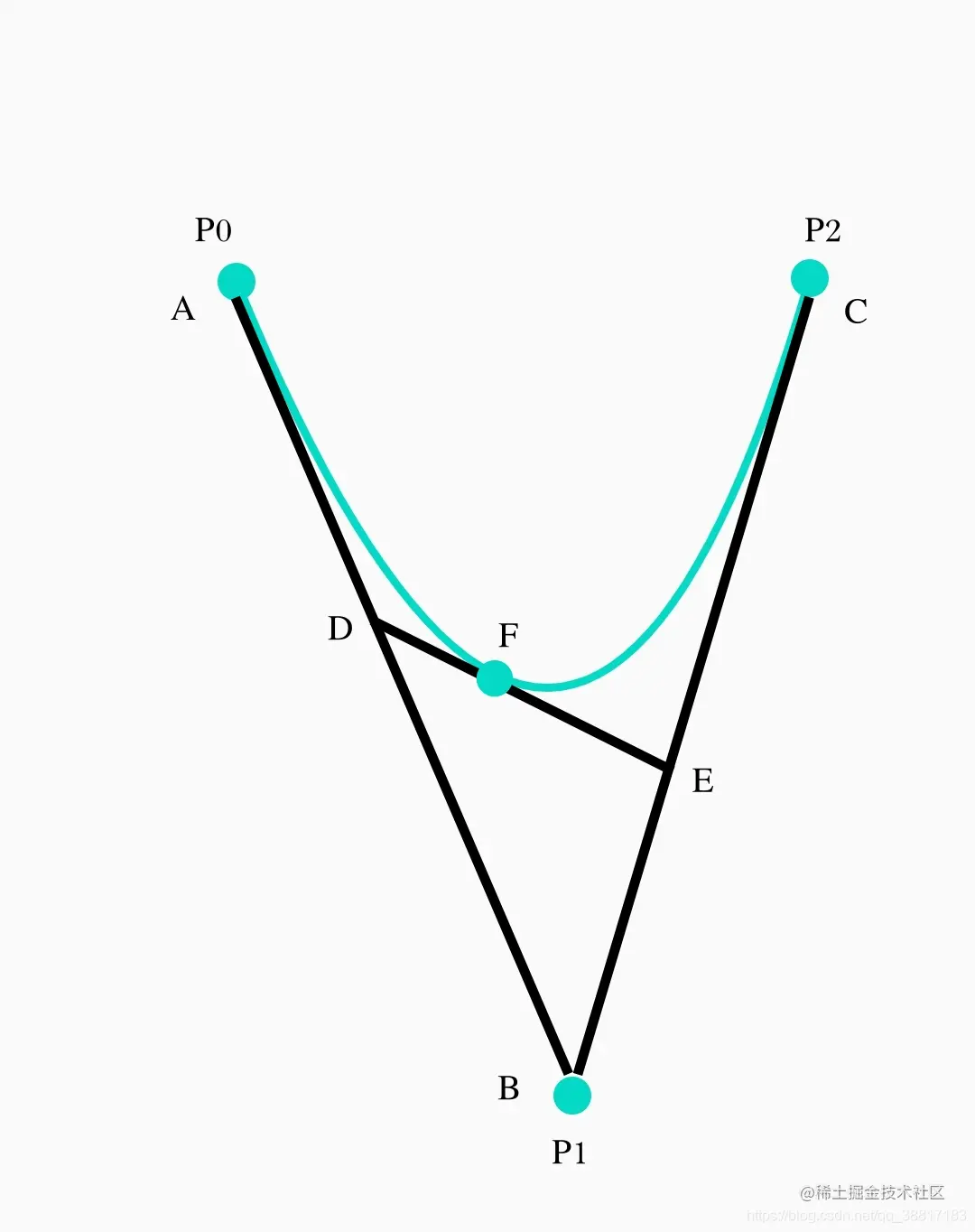
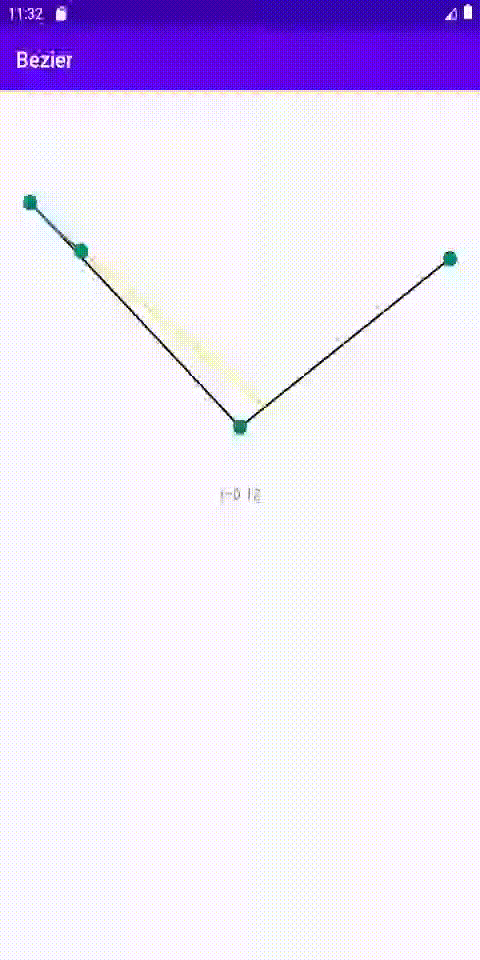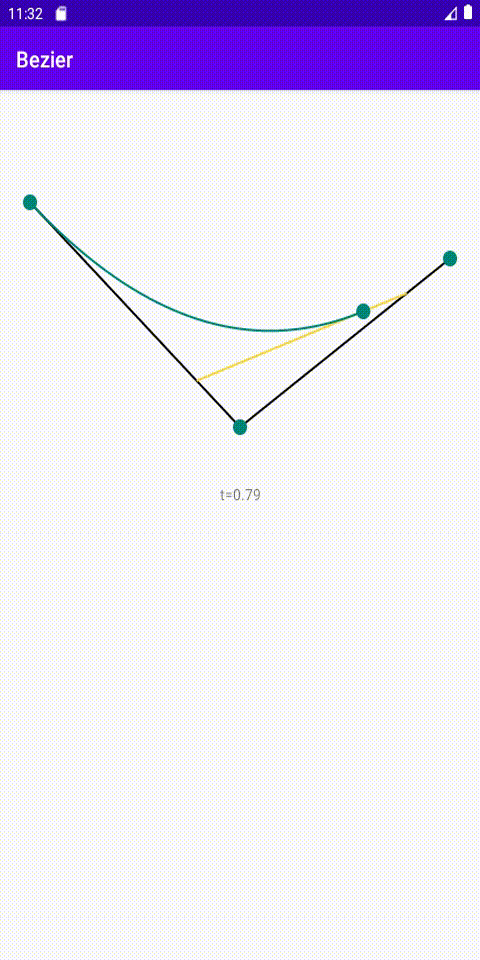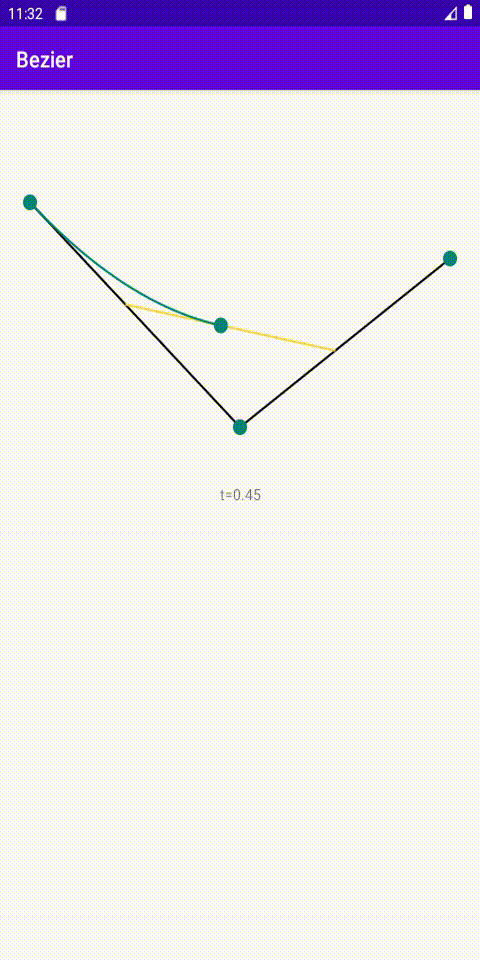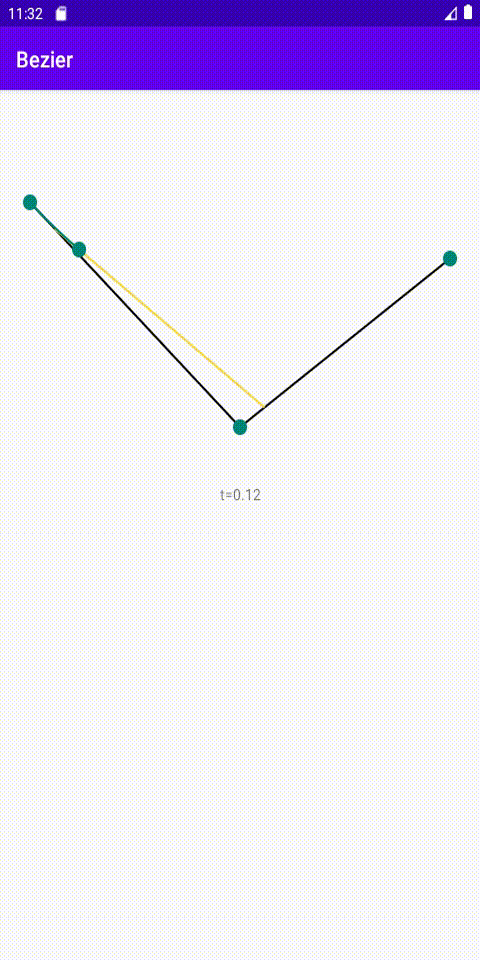
数学理论

• 连接$p_{0}$到$p_{1}$、$p_{1}$到$p_{2}$
• 在线段AB上找到点D，BC上找到点E，使得AD/AB=BE/BC=t,$t\epsilon [0,1]$
• 连接线段DE,在DE上找到点F,使得DF/DE=AD/AB=BE/BC=t,$t\epsilon [0,1]$
• t从0开始，线性缓慢变化到1，使用上述规则找出所有的点F，并将它们连接，最终得到二阶贝塞尔曲线

公式推导

二阶贝塞尔曲线可以看成是分别由前两个顶点（$p_{0}$,$p_{1}$）和后两个顶点（$p_{1}$,$p_{2}$）决定的一阶贝塞尔曲线的线性组合。 说的有点绕，我们知道贝塞尔函数其是一系列连续的点组成的曲线，我们可以将t值固定，先将 （$p_{0}$,$p_{1}$)代入一阶贝塞尔函数公式得到点D,再将（$p_{1}$,$p_{2}$）代入一阶贝塞尔函数公式得到点E,最后将得到的（D,E）再利用一次一阶贝塞尔函数，就得到了点F。接下来的步骤就很熟悉了，让t在[0，1]内线性增大，得到了一些列的F点，连起来就是我们的二阶贝塞尔曲线了。

• 由一阶贝塞尔曲线公式：$B(t)=(1-t)p_{0}+tp_{1},t\epsilon (0,1)$
• $p_{0}$替换为$B(t)=(1-t)p_{0}+tp_{1}$
• $p_{1}$替换为$B(t)=(1-t)p_{1}+tp_{2}$
• 可得到：$B(t)=(1-t)\left [ (1-t)p_{0}+tp_{1} \right ]+t\left [(1-t)p_{1}+tp_{2}\right ],t\epsilon (0,1)$
• 化简后就得到二阶贝塞尔函数：$B(t)=(1-t)^{2}p_{0}+2t(1-t)p_{1}+t^{2}p_{2},t\epsilon [0,1]$

1.3. 三阶贝塞尔曲线及n阶贝塞尔曲线

三阶贝塞尔曲线有两个控制点，其公式为：

$B(t)=p_{0}(1-t)^{3}+3p_{1}t(1-t)^{2}+3p_{2}t^{2}(1-t)+p_{3}t^{3},t\epsilon [0,1]$

其中$p_{0}$为起始点，$p_{1}$为控制点1，$p_{2}$为控制点2，$p_{3}$为结束点。

公式推导

按照二阶的推导原理，三阶贝塞尔曲线可被定义为分别由（$p_{0}$,$p_{1}$,$p_{2}$）和（$p_{1}$,$p_{2}$,$p_{3}$）确定的二阶贝塞尔曲线的线性组合：

$B^{3}(t)=(1-t)B_{(0,1,2)}^{2}(t)+tB_{(1,2,3)}^{2}(t),t\epsilon [0,1]$

其中$B^{n}(t)$代表n阶贝塞尔函数，$B_{(0,1,2)}^{2}$代表使用（$p_{0}$,$p_{1}$,$p_{2}$）点计算的二阶贝塞尔函数。 由此我们还可推出n阶贝塞尔函数公式：

$B^{n}(t)=\left\{\begin{matrix} p_{i},n=0 & \\ (1-t)B_{(0...n-1)}^{n-1}(t)+tB_{(1...n)}^{n-1}(t),n=[1,+\infty ]& \end{matrix}\right.$

（很明显可以用递归做）