如何使用Union Find算法检测无定向图中的周期

在这篇文章中，我们探讨了使用union-find算法检测无向图中的循环的方法。这需要O(VE)的时间复杂度：

目录
1)联合查找算法概述
2）简介
3)使用Union-Find算法查找周期的算法
4)通过例子理解算法
5)在Python中的实现
6)结论

1)联合查找算法概述

Disjoint-Set是用于Union-Find算法的数据结构。

Disjoint-Set的定义如下：

给定一个元素集。这些项目被划分为几个子集，使每个元素被限制在一个特定的子集中。

简单来说，Disjoint-Set数据结构是一组集合，其中没有两个集合包含相同的元素。

它也被称为联合-查找数据结构，因为它支持对子集的联合和查找操作。我们来理解这些术语。

查找：每个子集由该子集的一个元素代表，称为集合代表。该操作返回它所属的特定元素的集合代表。这个操作的最坏情况下的时间复杂度为 **O(N)**其中N是集合中的元素数，因为它是递归地找到集合代表的。

Union:在这个操作中，两个子集被合并为一个子集，合并后的子集的集合代表将是那些被合并的子集的集合代表中的一个。这个操作的时间复杂度为 O(1).

还有一个操作叫做make-set操作。

Mak-Set:这个操作为给定集合中的每个元素创建不相交的集合，每个不相交集合的集合代表将是其中包含的元素。这个操作的时间复杂度为 O(1).

这里每个子集都可以被称为不相交集。

2）简介

简单地说，如果存在一条起始顶点和结束顶点相同的路径，那么这个图就被称为循环图。

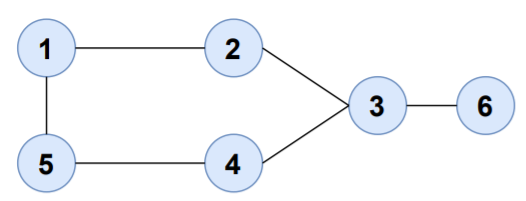
考虑一下路径:

1-2-3-4-5-1

开始和结束的顶点是相同的。因此，该图包含循环。

3)使用Union-Find找到循环的算法

对图中的每条边（u,v）重复以下步骤-如果u和v都属于同一个互不相干的集合，则图中存在循环

4）通过例子理解算法

让我们使用联合查找算法来查找无向图中的循环。

找出图中的边:

*1-2
2-3 3
-4 3-
6
4-5
1-5

由于有六个顶点，我们将创建六个不相交的集合:

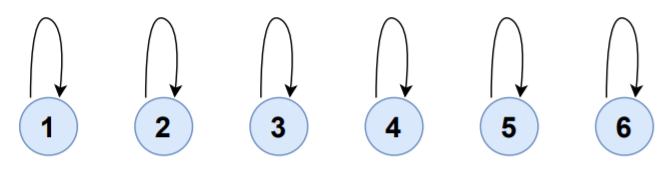
集合	元素	集合代表
S1	{1}	1
S2	{2}	2
S3	{3}	3
S4	{4}	4
S5	{5}	5
S6	{6}	6

考虑边1-2:

find(1)=1
find(2)=2

UNION(1,2)

S1,S2将被合并到S1，S1的集合代表现在是1:

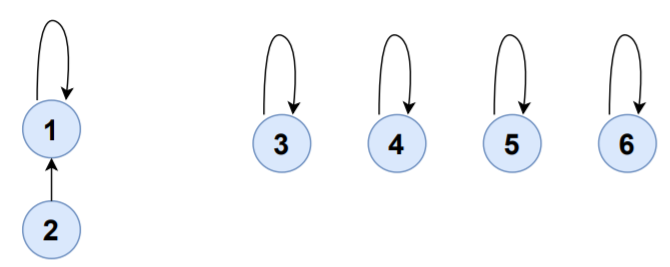
设置	元素	集合代表
S1	{1,2}	1
S3	{3}	3
S4	{4}	4
S5	{5}	5
S6	{6}	6

考虑边2-3:

find(2)=1
find(3)=3

UNION(1,3)

S1,S3将被合并到S1，S1的集合代表现在是1:

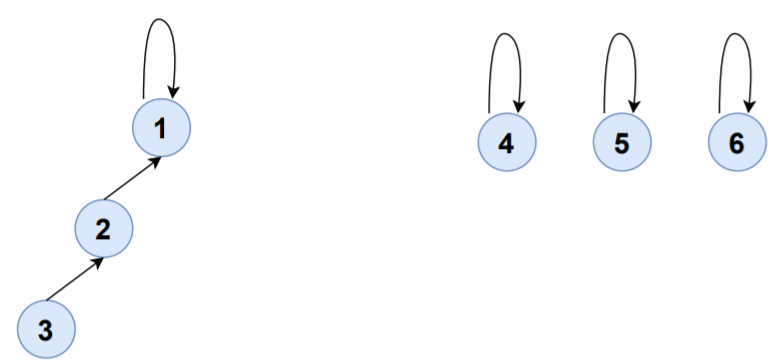
设置	元素	集合代表
S1	{1,2,3}	1
S4	{4}	4
S5	{5}	5
S6	{6}	6

考虑边3-4:

find(3)=1
find(4)=4

UNION(1,4)

S1,S4将被合并到S1，S1的集合代表现在是1。

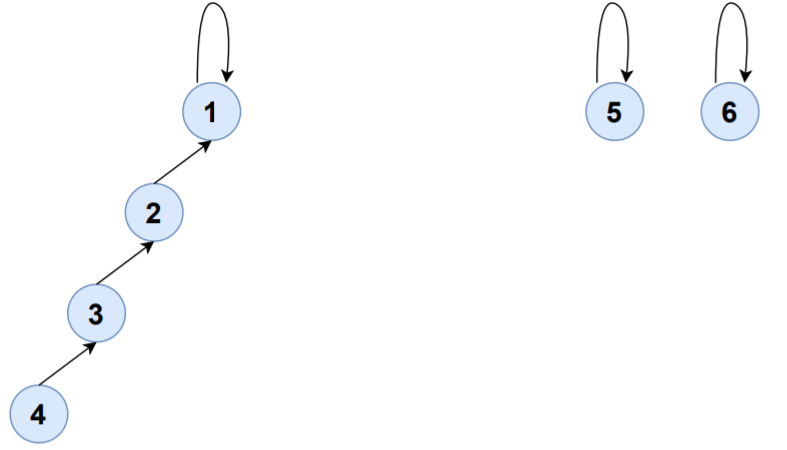
设置	元素	集合代表
S1	{1,2,3,4}	1
S5	{5}	5
S6	{6}	6

考虑边3-6:

find(3)=1
find(6)=6

UNION(1,6)

S1,S6将被合并到S1，S1的集合代表现在是1:

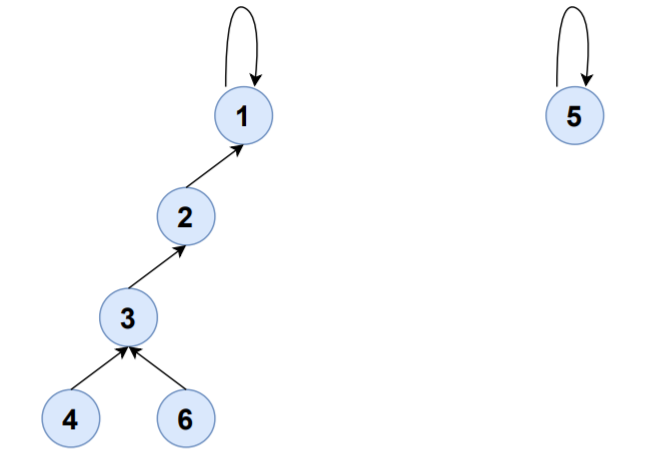
集合	元素	集合代表
S1	{1,2,3,4,6}	1
S5	{5}	5

考虑边4-5:

find(4)=1
find(5)=5

调用union(1,5)

S1,S5将被合并到S1，S1的集合代表现在是1:

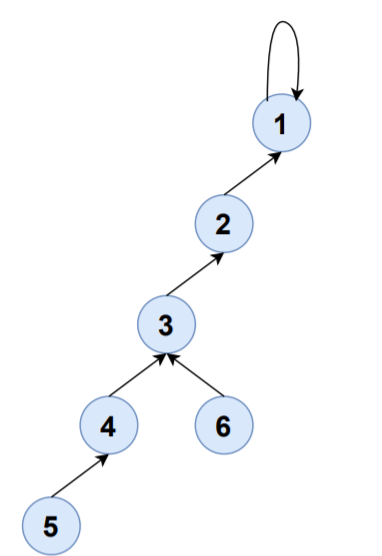
设置	元素	集合代表
S1	{1,2,3,4,5,6}	1

考虑边1-5:

find(1)=1
find(5)=1

这里FIND(1)=FIND(5)，意味着两者都属于同一个不相交的集合。因此，该图有一个循环:

5）用Python实现

class Union_Find:
    def make_set(self,n):
        self.disjoint_set={vertex:vertex for vertex in range(1,n+1)}#Initializing n subsets and make contained vertex itself the set-representative for each subset
    def find(self,vertex):
        if self.disjoint_set[vertex]==vertex:#A set-representative can be found if v:v
            return vertex
        return self.find(self.disjoint_set[vertex])
    def union(self,x,y):
        set_representative_X=self.find(x)#find set-representative of x
        set_representative_Y=self.find(y)#find set-representative of y
        self.disjoint_set[set_representative_Y]=set_representative_X#make set-representative of y as x

def isCyclic(edges,no_of_vertices):
    ds=Union_Find()
    ds.make_set(no_of_vertices)
    for x,y in edges:
        if ds.find(x)==ds.find(y):#if set-representatives of both the vertices are the same then cycle exists
            print("Cycle exists in the graph!")
            return
        ds.union(x,y)#merge subsets x and y
    print("Cycle doesn't exist in the graph!")
V=int(input())
E=int(input())
edges=[]
for t in range(E):
    x,y=[int(x) for x in input().split()]
    edges.append([x,y])
isCyclic(edges,V)

输入:

V=6
E=6
edges=[[1,2],[2,3],[3,4],[3,6],[4,5],[1,5]]

输出:

Cycle exists in the graph!

考虑不包含循环的图形:

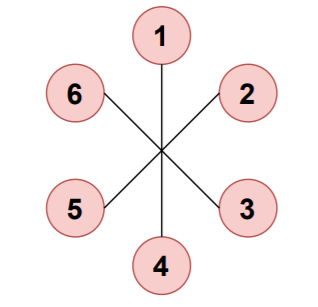
输入: 输出: 考虑不包含循环的图:

V=6
E=6
edges=[[1,4],[2,5],[3,6]]

输出:

Cycle doesn't exist in the graph!

6)结论

联合查找算法的时间复杂度为 O(V)，其中V是图中的顶点数量，在最坏的情况下。

由于我们需要访问每条边，所以需要的时间为 O(E)其中E是图中的边的数量。

因此，使用Union-Find检测无定向图中的周期的总体时间复杂度为 O(VE).

在这种情况下，V是顶点的数量，E是边的数量。在密集图的情况下，E的数量为O(V2)。因此，在密集图中，这种方法需要O(V3)的时间复杂度。

通过OpenGenus的这篇文章，你一定对如何使用Union Find算法检测无定向图中的周期有了完整的认识。