线性模型

iGxnon
95 阅读1分钟

f(x) = ωTx + bf(x) = \mathbf{\omega}^Tx + b

线性回归

线性回归模型试图学习出一个线性关系进行预测

求解线性回归模型

单元线性回归

(w∗,b∗) = arg⁡min⁡(w,b) ∑i=1m(yi−wxi−b)2(w^*, b^*) = \underset{(w, b)}{\arg{\min}} \sum_{i=1}^m(y_i - w x_i -b)^2

  • 基于均方误差 (MSE) 最小化求得模型的最优解 (最小二乘法)
  • b = 1m ∑i=1m (yi−wxi)b = \frac{1}{m} \sum_{i=1}^m (y_i - w x_i)
  • w=∑i=1myi(xi−xˉ)∑i=1mxi2−1m(∑i=1mxi)2 w = \frac{\sum_{i=1}^m y_i(x_i - \bar{x})}{\sum_{i=1}^m x_i^2 - \frac{1}{m}(\sum_{i=1}^m x_i)^2} 

多元线性回归

对于多元的 xx ，此时 xx  会形成一个矩阵，而不是一个列向量

令 X=(x1T1x2T1......xmT1)X = \begin{pmatrix} x_1^T & 1 \\ x_2^T & 1\\ ... & ...\\ x_m^T & 1 \end{pmatrix} , w^ = (w;b)\hat{w} = (w; b) ，这样有多元线性回归 f(X) = Xw^f(X) = X\hat{w}

有 w^∗ = arg⁡min⁡w^ (y − Xw^)T(y − Xw^)\hat{w}^* = \underset{\hat{w}}{\arg\min} (\mathbf{y} - X\hat{w})^T(\mathbf{y} - X\hat{w})  (为了矩阵可以相乘，这里需要加上个转置)

对右式进行求导令其等于0：  2XT(Xw^ − y) = 02X^T(X\hat{w} - y) = 0

当 XTXX^TX  为满秩矩阵时，有 w^∗ = (XTX)−1XTy\hat{w}^* = (X^TX)^{-1}X^Ty

最终得到的模型时 f(x^i) = x^iT (XTX)−1XTyf(\hat{x}_i) = \hat{x}_i^T (X^TX)^{-1}X^Ty

但实际情况下 , XTXX^TX  基本上不会是满秩，那么 w^∗\hat{w}^*  就有多个解，每一个解都可以使均方误差最小化

常见的做法是引入正则化 (regularization) 项

对数线性回归(log-linear regression)

很多情况下数据并不是按照线性进行变化的，如培养皿中细菌的数量变化，这往往是指数型的

可以令模型的预测值去逼近 y 的衍生物，比如指数型变化的 y，那么 lnylny  就是线性变化的

lny = wTx + blny = w^Tx + b  这就是对数线性回归

它实际上拟合的是 y=ewTx+by = e^{w^Tx + b}  这种关系

广义上，可以将这种关系推广

形成 y = g−1(wTx+b)y = g^{-1}(w^Tx + b)  这种广义上的线性模型，其中 g(x)g(x)  称为联系函数， 需要是连续可微的

对数几率(线性)回归(logistic regression)

有的时候会称其为逻辑回归(logit regression)

当希望线性模型可以用于分类任务(主要针对二分类)的话，可以使用对数几率回归

对于 z = wTx + bz = w^Tx + b  的输出，可以令 y = 11+e−zy = \frac{1}{1+ e^{-z}} ，有 y = 11+e−(wTx + b)y = \frac{1}{1+ e^{-(w^Tx + b)}}

有 ln y1−y = wTx + bln \frac{y}{1-y} = w^Tx + b ，其中的对数几率函数( g−1(x)g^{-1}(x) ) y = 11+e−zy = \frac{1}{1+ e^{-z}} ，也可以被称为 Sigmoid 函数 (形状类似于 S 的函数)

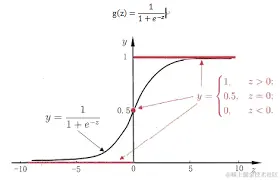
名称由来： y1−y\frac{y}{1-y} ，其中 yy  可以认为是被认为是正例的概率，则 1 − y1 - y  是被认为是反例的概率，二者的比值叫说 几率，对其取对数，叫做 对数几率

求解模型

将 y 视为概率后，有 ln p(y=1∣x)p(y=0∣x) = wTx + bln \frac{p(y=1 | x)}{p(y=0|x)} = w^Tx + b

有 p(y=1∣x) = ewTx+b1+ewTx+bp(y=1|x) = \frac{e^{w^Tx + b}}{1 + e^{w^Tx+b}} , p(y=0∣x) = 11+ewTx+bp(y=0|x) = \frac{1}{1 + e^{w^Tx+b}}

通过最大似然估计，对于给定数据集 {(xi,yi)}i=1m\{(\mathbf{x_i}, y_i)\}_{i=1}^{m}

有模型的对数似然 ℓ (w,b) = ∑i=1mln⁡p(y=yi∣xi;w,b)\ell (w, b) = \sum_{i=1}^{m}\ln{p(y=y_i|x_i; w,b)}

令 β = (w;b), x^ = (x;1)\beta = (w; b), \hat{x} = (x; 1) ，有 wTx + b = β Tx^w^Tx + b = \beta ^T\hat{x} ，再令 p1(x^; β) = p(y=1∣x^; β)p_1(\hat{x}; \beta) = p(y=1|\hat{x}; \beta)

同理 p0(x^; β) = p(y=0∣x^; β) = 1− p1(x^; β)p_0(\hat{x}; \beta) = p(y=0|\hat{x}; \beta) = 1- p_1(\hat{x}; \beta)

那么有 p(y=yi∣xi;w,b)={p1(x^i;β)yi=1p0(x^i;β)yi=0=yip1(x^i;β)+(1−yi)p0(x^i;β)p(y=y_i|x_i; w,b) = \begin{cases} p_1(\hat{x}_i; \beta) & y_i=1\\ p_0(\hat{x}_i; \beta) & y_i=0 \end{cases} = y_ip_1(\hat{x}_i; \beta) + (1-y_i)p_0(\hat{x}_i; \beta)

然后结合上面各式 ℓ(β) = ∑i=1m(−yiβTx^i + ln⁡(1+eβTx^i))\ell(\beta) = \sum_{i=1}^{m}(-y_i\beta^T\hat{x}_i + \ln(1+e^{\beta^T\hat{x}_i}))  最大化该式即可 β∗ = arg⁡min⁡βℓ(β)\beta^* = \underset{\beta}{\arg\min} \ell(\beta)

可以用梯度下降(gradient descent)，牛顿法等方法

线性判别分析(Linear Discriminant Analysis LDA)

也称  “Fisher” 判别分析

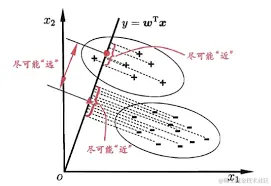
和 PCA 很像，对于给定训练集，将数据投影到一条直线上，使同类的投影点在直线上的距离尽可能靠近，不同类的投影点的中心点尽可能远离，进行预测时，将数据投影到拟合的直线上，根据距离来分类

推导

给定 D = {(xi. yi)}i=1m  yi ∈ {0, 1}D = \{(\mathbf{x}_i. y_i)\}_{i=1}^m \quad y_i \in \{0, 1\}  (其中 xi\mathbf{x}_i 是一个随机变量的向量)

有 Xi, μi, Σi\mathbf{X_i, \mu_i, \Sigma_i}  分别表示第 i∈{0,1} i\in\{0,1\}  类的 数据矩阵、均值向量、协方差矩阵

y = ωTxy = \mathbf{\omega}^Tx  表示所拟合的直线 (这里不需要偏移量 bias )

那么两类样本在直线上的中心点为 ωTμ0，ωTμ1\mathbf{\omega^T\mu_0}，\mathbf{\omega^T\mu_1} ，投影后，两类样本的(协)方差变成了 ωTΣ0ω，ωTΣ1ω\mathbf{\omega^T\Sigma_0\omega}，\mathbf{\omega^T\Sigma_1\omega} ，不难得出，上面四个表达式都是标量

要使同类之间的距离尽可能小，即 ωTΣ0ω，ωTΣ1ω\mathbf{\omega^T\Sigma_0\omega}，\mathbf{\omega^T\Sigma_1\omega}  尽可能小，也就是 ωTΣ0ω + ωTΣ1ω\mathbf{\omega^T\Sigma_0\omega} + \mathbf{\omega^T\Sigma_1\omega}  尽可能小，要使异类之间的距离尽可能大，即 ∣∣ωTμ0 − ωTμ1∣∣22 = (ωTμ0 − ωTμ1)2||\mathbf{\omega}^T\mu_0 - \omega^T\mu_1||_2^2 = \mathbf{(\omega}^T\mu_0 - \omega^T\mu_1)^2  尽可能大

综合二者，有 J = ∣∣ωTμ0 − ωTμ1∣∣22ωTΣ0ω + ωTΣ1ω = ωT(μ0 − μ1)(μ0 − μ1)TωωT(Σ0+Σ1)ωJ = \frac{||\mathbf{\omega}^T\mu_0 - \omega^T\mu_1||_2^2}{\mathbf{\omega^T\Sigma_0\omega} + \mathbf{\omega^T\Sigma_1\omega}} = \mathbf{\frac{\omega^T(\mu_0 - \mu_1)(\mu_0 - \mu_1)^T\omega}{\omega^T(\Sigma_0+\Sigma_1)\omega}} 最大化

求解

令 Sω= Σ0+Σ1  Sb = (μ0−μ1)(μ0−μ1)T\mathbf{S_\omega = \Sigma_0+\Sigma_1 \quad S_b = (\mu_0-\mu_1)(\mu_0-\mu_1)^T} ，有 J = ωTSbωωTSωωJ = \mathbf{\frac{\omega^T S_b\omega}{\omega^TS_\omega\omega}} ，需要从中求解出 ω\omega ，观察上式， ω = ω∗\omega = \omega^*  和 ω = kω∗ (k∈ R , k≠0)\omega = k\omega^* (k \in R , k\not=0)  都是 JJ  最大化时的解，即 ω\omega 与大小无关，只取决于它的方向

不妨令 ωTSωω = 1\omega^TS_\omega\omega = 1  作为前提条件，那么求解问题就等价于 min⁡ω −ωTSbω  s.t.   ωTSωω = 1\underset{\omega}{\min} -\omega^TS_b\omega \quad s.t.   \omega^TS_\omega\omega = 1

由拉格朗日乘子法，当到达最优解 ω = ω∗\omega = \omega^*  时，函数 f(ω) = −ωTSbωf(\omega) = -\omega^TS_b\omega  在约束平面 g(ω) = ωTSωω − 1g(\omega) = \omega^TS_\omega\omega - 1  上最优解点的梯度 ∇f(ω∗) = λ∇g(ω∗)\nabla{f(\omega^*)} = \lambda\nabla{g(\omega^*)} ， λ \lambda  是拉格朗日乘子，等价于求解 f(ω) = λg(ω)f(\omega) = \lambda g(\omega)  取最值时， ω\omega  的取值即为 ω∗\omega^* ，又由于 ω\omega  与大小无关，只与方向有关，可以令 h(ω) = g(ω) + 1 = ωTSωωh(\omega) = g(\omega) + 1 = \omega^TS_\omega\omega ，于是就等价于求解

f(ω)= λh(ω)   ⟺  ωTSbω = λωTSωω   ⟺   Sbω = λSωωf(\omega) = \lambda h(\omega) \iff \omega^TS_b\omega = \lambda\omega^TS_\omega\omega \iff S_b\omega = \lambda{S}_\omega\omega

考虑到 Sbω = (μ0−μ1)(μ0−μ1)Tω = (μ0−μ1)∗[(μ0−μ1)Tω]S_b\omega = (\mu_0-\mu_1)(\mu_0-\mu_1)^T\omega = (\mu_0-\mu_1)*[(\mu_0-\mu_1)^T\omega] ， 其中 [(μ0−μ1)Tω][(\mu_0-\mu_1)^T\omega]  是一个标量，于是 SbωS_b\omega  始终和 (μ0−μ1)(\mu_0-\mu_1)  一个方向，不妨令 Sbω = k(μ0−μ1)S_b\omega = k(\mu_0-\mu_1) ，于是有

k(μ0−μ1) = λSωωk(\mu_0-\mu_1) = \lambda{S}_\omega\omega ，考虑到 ω\omega  与方向无关，那么 k, λk, \lambda  都可以省去，有 ω = Sω−1(μ0 − μ1)\omega = S_\omega^{-1}(\mu_0 - \mu_1)

实际情况下，求解 Sω−1S_\omega^{-1} 有很多方法，最常见的就是“奇异( 特征 )值分解”，将 SωS_\omega  化成 VΣVTV\Sigma V^T ，其中 Σ\Sigma  是由 SωS_\omega  的奇异值构成的对角矩阵，然后由 Sω−1 = VΣ−1VTS_\omega^{-1} = V\Sigma^{-1}V^T  求出 Sω−1S_\omega^{-1}

推广

可以将 LDA 推广到多分类问题上，假设有 NN  个类别，第 ii 个类别有 mim_i  个类别数，此时 SωS_\omega  推广到了每个类别的协方差矩阵之和，即 Sω =∑i=1mi Sωi=∑i=1mi∑x∈Xi(x−μi)(x−μi)TS_\omega = \mathbf{\sum_{i=1}^{m_i} S_{\omega i}=\sum_{i=1}^{m_i}\sum_{x\in X_i}(x-\mu_i)(x-\mu_i)^T} ，用于衡量各个类内部的方差(散度)大小， μi\mu_i  表示第 ii  类的均值向量

此时 SbS_b  可以推广为 Sb = ∑i=1N mi(μi−μ)(μi−μ)TS_b = \mathbf{\sum_{i=1}^{N} m_i(\mu_i-\mu)(\mu_i-\mu)^T} ，用于衡量各个类之间的方差(散度)大小，其中 μ\mu  表示所有类的平均均值向量

另外再定义一个 St = Sb + Sω = ∑i=1mi(xi−μ)(xi−μ)TS_t = S_b + S_\omega = \sum_{i=1}^{m_i}(x_i-\mu)(x_i-\mu)^T ，衡量全局散度 

此时求解 LDA 中的 ω\omega  可以由 Sω, Sb, StS_\omega, S_b, S_t  三者中任意两个都可以

常见优化下面的目标

W∗ = arg⁡max⁡Wtr(WTSbW)tr(WTSωW)\mathbf{W^* = \underset{W}{\arg\max}\frac{tr(W^TS_bW)}{tr(W^TS_\omega W)}} ，其中 W\mathbf{W} 可以是一个"降维矩阵"， 将高维的数据降维分类 ；  tr(∗)tr(*)  表示矩阵的迹(trace)

最后转换成对广义特征值求解： SbW=λSωW\mathbf{S_bW = \lambda S_\omega W}

多分类学习

生活中常见的分类任务大多数都是多分类的，虽然有一些方法可以直接推广到多分类，例如 LDA，但是大多数情况下，一般是基于一些规则，利用二分类模型来解决多分类问题

拆分策略

将多分类任务进行拆分，训练多个二分类模型来处理

  • 一对一 (One vs. One OvO)

    • 将 N 个类别分别两两配对，产生 CN2 = N(N−1)2C_N^2 = \frac{N(N-1)}{2}  个二分类任务，测试阶段时，将数据给这些分类器分类进行投票，最多的分类结果作为最终分类结果

  • 一对多 (One vs. Rest OvR)

    • 每次将一个类的样本作为正例，其余的作为反例，N 个类别就可以训练 N 个分类器，测试时如果只有一个分类器预测为正类，那么就采取这个分类器的正类作为最终分类结果，如果有多个分类器都预测为正类，则需要结合分类器的置信度来判断最终分类结果

  • 多对多 (Many vs. Many MvM)

    • 每次将若干个作为正例，若干个作为反例进行训练，MvM 选取正反例时不能随意选取，需要按照一定的规则

纠错输出码 (Error Correcting Output Codes. ECOC)

  • 编码：对 N 个类别做 M 次划分，每次划分后，一部分作为正类，另一部分作为反类；这样一共可以训练 M 个二分类模型
  • 解码：M 个分类器对测试数据进行预测，根据这些预测结果的标记组成一个编码， 将这个预测的编码与每个类别的编码进行比较，返回其中距离最近的类别作为最终预测结果

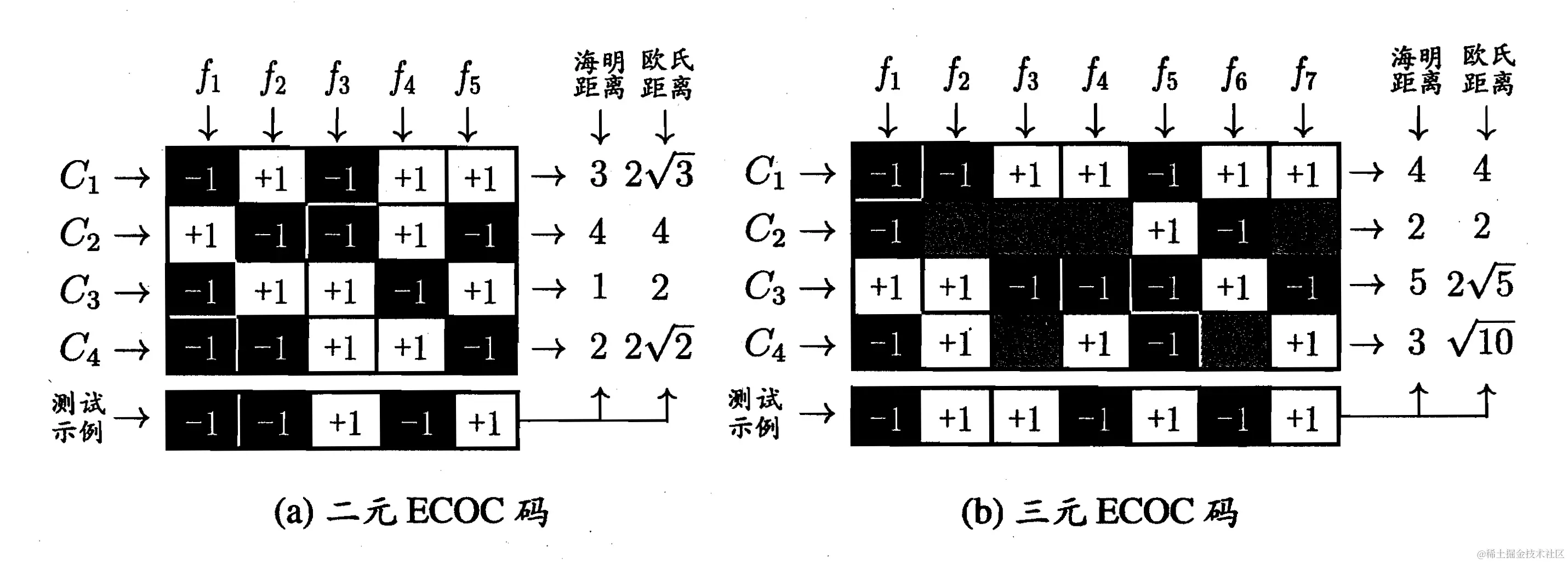
其中 fif_i  表示分类器，在三元 ECOC 码中，图中全黑部分表示这个类别不参与该分类器的训练，并且一般标记为 0

ECOC 编码对某个分类器分类错误具有一定修正，容忍能力，当 ECOC 编码越长(分类器越多)，纠错的能力就越强

ECOC 编码设计时，不同类别之间的编码距离越远，纠错能力就越强，在码长较小时可以使用这个原则设计出最优编码

类别不平衡问题

分类问题在实际情况下经常遇到类别不平衡问题，例如诊断一个人是否患人群中的某种遗传病，其训练样本绝大多数都是不患病，只有少量患病的样本；这时分类器只需要将所有数据都预测为不患病，最后的精度依旧很高

对于线性分类器(逻辑回归)，输出的标号 yy  可以作为一个预测为正类的概率，那么 y1−y \frac{y}{1-y}   表示预测正类和反类之间的概率比值。对于类别平衡的情况 y1−y > 1\frac{y}{1-y} > 1  时，就将类别判断为正例

对于类别不平衡的情况，若有 m+m^+  个正例样本， m−m^-  个反例样本，那么当 y1−y > m+m− \frac{y}{1-y} > \frac{m^+}{m^-}   时才判断为正例会更好；即分类器预测的概率需要高于观测概率

实际情况下，对于每一个任务都去修改分类器的阈值很麻烦，实际上只需要对输出进行缩放(乘上 m−m+\frac{m^-}{m^+} )即可，这个基本策略称为——再缩放

不过实际情况下，训练样本的观测概率往往和现实中的实际概率不相同，那么训练出的模型应用于实际效果却不好，这时候通常有三种做法：欠采样，过采样，阈值转移

  • 欠采样

    • 去除多余的类别的样本，来让正反例样本数目相当

      • 利用集成学习，将数目较多的类别分为几个和另一个类别数目相当的数据集，组合它们形成不同的正反例数据集，训练多个模型

  • 过采样

    • 增加较少样本的类别，让正反例样本数目相当

    • SMOTE 算法

      • 对数据进行插值来产生额外的数据

  • 阈值转移

    • 在原始数据集中训练出模型，实际使用进行决策时动态调整阈值
avatar
文章
阅读
粉丝