携手创作，共同成长！这是我参与「掘金日新计划 · 8 月更文挑战」的第1天，点击查看活动详情

问题

该任务是根据房屋信息预测房屋销售价格，例如卧室、生活区、位置、学校附近以及卖家摘要。数据包括2020年加利福尼亚州售出的房屋，测试数据集中的房屋在训练数据集中的房屋之后售出。此外，私人排行榜房屋在公共排行榜房屋之后出售。

kaggle 地址：www.kaggle.com/competition…

模型

在这个任务上，你会发现很多因素都会影响着房价，例如房间面积，房龄等，当把这些因素设置为变量 $X$ ，房价设置为 $Y$ ，就可以写成如下面的模型

\mathrm{price} = w_{\mathrm{area}} \cdot \mathrm{area} + w_{\mathrm{age}} \cdot \mathrm{age}+... + b.

说明： $w_{\mathrm{area}}$ , $w_{\mathrm{age}}$ 是权重， $b$ 则是偏置。

当权重发生变化时候，房价也会跟着改变，问题来了，权重是多少呢？怎么设置权重呢？

其实我们可以拿到数据集，可以通过拟合数据集得到权重和偏置，就可以得到我们想要的值。后续的所有的过程和函数，都是帮助学习权重和偏置，用于模型预测。

不同组合的权重与偏置，计算出来的房价与实际值会存在一定偏差，这个偏差是能够去判定选择权重与偏置拟合程度怎么样的。损失函数是能够量化目标实际值与预测值的之间的差距。怎么定义问题的损失函数呢？

有正负数是不好去评判的，一般选择非负数作为参考，同时我们会希望针对整个模型，偏差越小越好，完美的拟合的损失为 0.

在线性回归模型中，最常用的损失函数是平方误差函数。当样本 $i$ 的预测值为 $\hat{y}^{(i)}$ ，其相应的真实标签为 $y^{(i)}$ 时，平方误差可以定义为以下公式：

l^{(i)}(\mathbf{w}, b) = \frac{1}{2} \left(\hat{y}^{(i)} - y^{(i)}\right)^2.

$\frac{1}{2}$ 仅仅是为了让后面的求导更加方便。

为了度量整个模型在数据集上的质量，我们需要记录每一个点的误差，求数据集误差的均值。

L(\mathbf{w}, b) =\frac{1}{n}\sum_{i=1}^n l^{(i)}(\mathbf{w}, b) =\frac{1}{n} \sum_{i=1}^n \frac{1}{2} \left(\hat{y}^{(i)} - y^{(i)}\right)^2.

模型图如下：

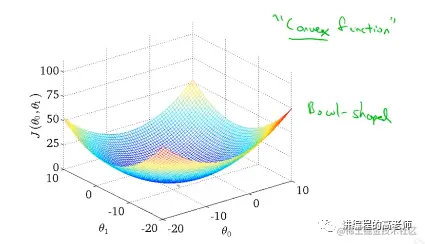
我们所期望的是找到合适的权重和偏置，可以让损失函数走到上图中的最小点，也就是最优的地方。

这里就有问题：怎么去找呢？哪个方向？

梯度下降就是用来求解凸优化问题的。它是通过一步步迭代求解，不断逼近正确结果，直到与真实值之差小于一个阈值，从而得到最小化损失函数的模型参数值的。公式如下：

\theta_{j}:=\theta_{j}-\alpha \nabla_{\theta_{j}} J(\theta)

根据问题，我们可以得知关于我们需要求解的权重与偏置的公式了。

\begin{array}{l} w=w-\alpha \frac{\partial}{\partial w} J(w, b) \\ b=b-\alpha \frac{\partial}{\partial b} J(w, b) \end{array}

我们已知：

L(\mathbf{w}, b) =\frac{1}{n}\sum_{i=1}^n l^{(i)}(\mathbf{w}, b) =\frac{1}{n} \sum_{i=1}^n \frac{1}{2} \left(\hat{y}^{(i)} - y^{(i)}\right)^2.

求偏导可得：

\begin{array}{l} \frac{\partial}{\partial w} J(w, b)=\frac{1}{m} \sum_{i=1}^{m}\left(f_{w, b}\left(x^{(i)}\right)-y^{(i)}\right) x^{(i)} \\ \frac{\partial}{\partial b} J(w, b)=\frac{1}{m} \sum_{i=1}^{m}\left(f_{w, b}\left(x^{(i)}\right)-y^{(i)}\right) \end{array}

经过上面的几个公式，你不断的迭代是可以获得一个拟合度比较高的权重与偏置，到此线性回归模型已经讲完了。

如果你对偏导不会求解，看看下面图片你就会理解了：

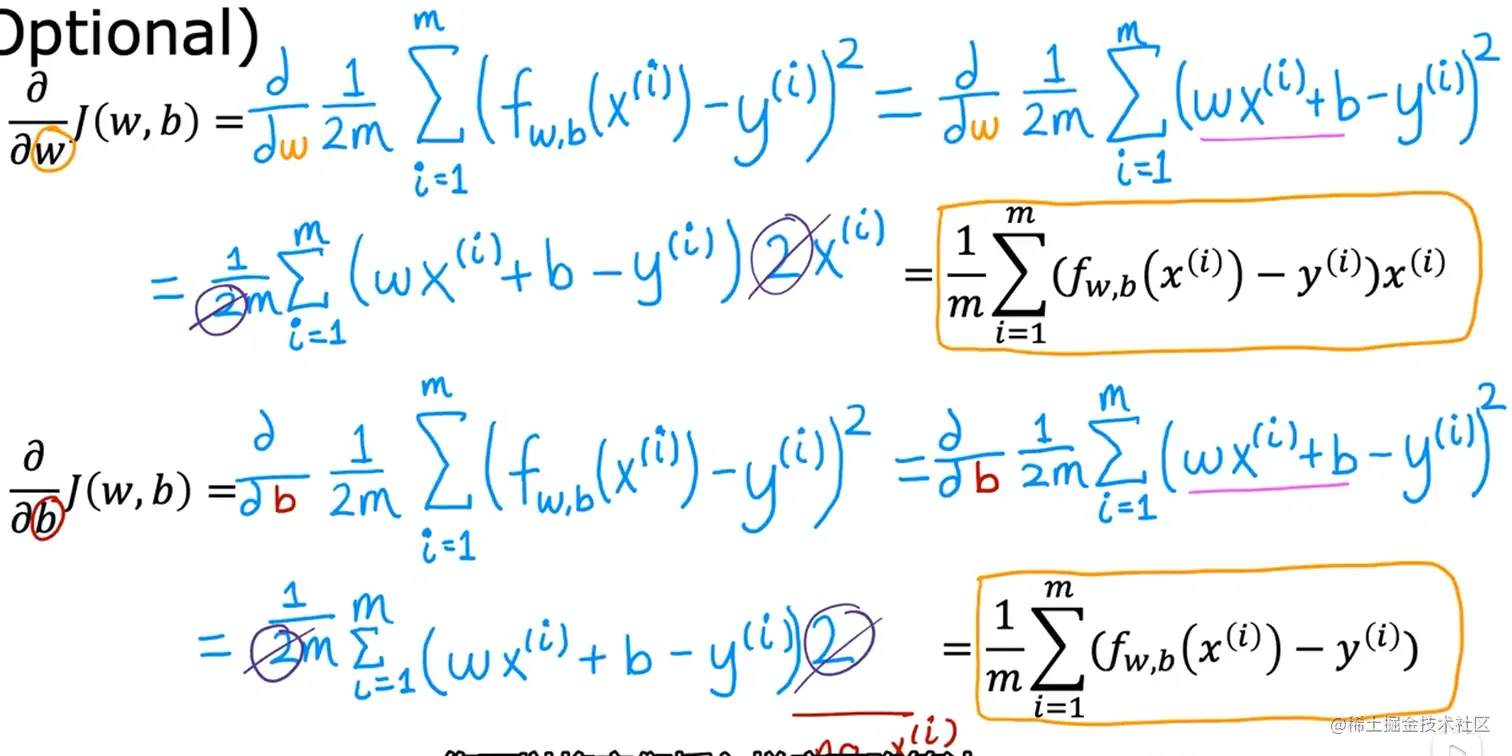
梯度下降

是什么？

梯度下降法（Gradient Descent，GD）是一种常用的求解无约束最优化问题的方法，在最优化、统计学以及机器学习等领域有着广泛的应用。

无约束最优化问题：指的是从一个问题的所有可能的备选方案中，选择出依某种指标来说是最优的解决方案。简单讲就是在一堆的答案中，找一个最优的答案，这不就是我们所期待的吗！我们就是期望能够在损失函数中找到最小点。

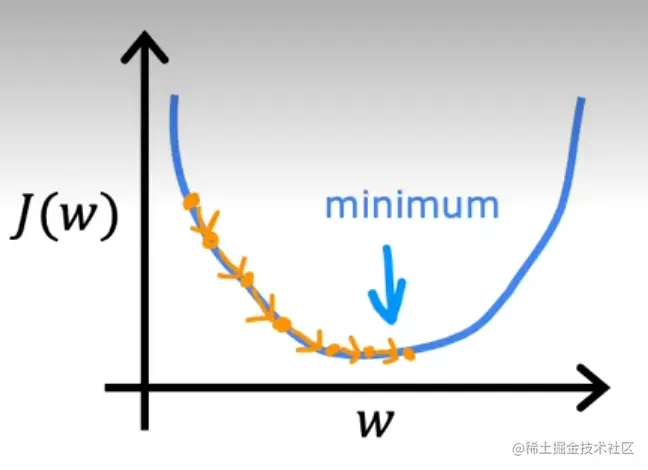从初始值到最低点，我们需要确定方向与距离，能帮助我们最快到达最低点。

方向：最陡峭的方向：梯度。
距离：先距离长，再慢慢减少。

过程简单讲：在某一个点处，设置你的步长，根据你的梯度的反向进行移动，这样子重复过程，你就会达到一个最低点，也是我们所期待的值。

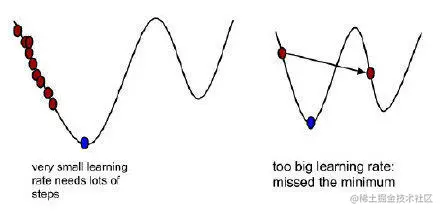
$\alpha$ 指学习率，可以理解成步长。只有设置合适的学习率才会更好的走到最低点。如果学习率较小，移动步数太多了，消耗很多的资源。如果学习率比较大，估计永远不会到达最低点，跨过去了。

$\nabla_{\theta_{j}} J(\theta)$ ，就是梯度，可以理解成方向。在一元函数中，梯度其实就是微分，既函数的变化率，而在多元函数中，梯度变为了向量，同样表示函数变化的方向，从几何意义来讲，梯度的方向表示的是函数增加最快的方向。梯度前面的符号为“-”，代表梯度方向的反方向。

怎么用？

根据计算梯度时候的所用数据量不同，可以分为三种：

批量梯度下降法（Batch Gradient Descent, BGD）

使用全部样本数据去计算。

\frac{\partial J(\Theta)}{\partial \theta_{j}}=\frac{1}{n} \sum_{i=1}^{n}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)}

小批量梯度下降法（Mini-batch Gradient Descent, MBGD）

随机选择一部分样本数据。

\frac{\partial J(\Theta)}{\partial \theta_{j}}=\frac{1}{k} \sum_{i}^{i+k}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)}

随机梯度下降法（Stochastic Gradient Descent, SGD）

选择其中一个样本数据。

\frac{\partial J(\Theta)}{\partial \theta_{j}}=\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)}

三种方法优缺点对比：

	BGD（批量）	SGD（随机）	MBGD（小批量）
优点	非凸函数可保证收敛至全局最优解	计算速度快	计算速度快，收敛稳定
缺点	计算速度缓慢，不允许新样本中途进入	计算结果不易收敛，可能会陷入局部最优解中	—

参考：

zhuanlan.zhihu.com/p/48205156

www.jianshu.com/p/424b7b70d… blog.csdn.net/qq_41800366… www.bilibili.com/video/BV1Pa…