动态规划（三）【打家劫舍】

打家劫舍Ⅰ

题目描述

解题思路1

基本上涉及到最优子问题的题目，都可以考虑使用动态优化。根据题意可以先列出结果方程：$dp(n)=amount$，方程含义为偷到第n间屋子偷窃到的最大金额为amount。接着可以列出状态转移方程$dp(n)=max(dp(n-2)+nums[n],dp[n-1])$

代码实现

from typing import List


class Solution:
    def rob(self, nums: List[int]) -> int:
        n = len(nums)
        n = len(nums)
        if n == 0:
            return 0
        if n == 1:
            return nums[0]
        dp_pre_1 = max(nums[0], nums[1])  # 前一间
        dp_pre_2 = nums[0]  # 前两间
        for i in range(2, n):
            dp_i = max(dp_pre_1, dp_pre_2+nums[i])
            dp_pre_2 = dp_pre_1
            dp_pre_1 = dp_i
        return dp_pre_1

提交结果：

解题思路2

$dp[i][0]=dp[i-1][1] + nums[i]$ ，表示第i间房子偷

$dp[i][1]=max(dp[i-1][0], dp[i-1][1])$，表示第i间房子不偷

代码实现

class Solution:
    def rob(self, nums: List[int]) -> int:
        n = len(nums)
        dp_0 = nums[0] # 偷
        dp_1 = 0  # 不偷
        for i in range(1, n):
            p = nums[i]
            dp_0, dp_1 = dp_1+p, max(dp_0, dp_1)
        return max(dp_1, dp_0)

提交结果：

打家劫舍Ⅱ

题目描述

解题思路

跟上题相比，列表首尾的房子也是相邻的。实际上我们可以将这个问题简化为nums[:-1]和nums[1:]两个子问题的结果。

代码实现1

class Solution:
    def rob(self, nums: List[int]) -> int:
        if len(nums) == 1:
            return nums[0]
        
        return max(self._rob(nums[1:]), self._rob(nums[:-1]))

    def _rob(self, nums: List[int]) -> int:
        n = len(nums)
        if n == 0:
            return 0
        if n == 1:
            return nums[0]
        dp_pre_1 = max(nums[0], nums[1])  # 前一间
        dp_pre_2 = nums[0]  # 前两间
        for i in range(2, n):
            dp_i = max(dp_pre_1, dp_pre_2+nums[i])
            dp_pre_2 = dp_pre_1
            dp_pre_1 = dp_i
        return dp_pre_1

提交结果1：

代码实现2

class Solution:
    def rob(self, nums: List[int]) -> int:


        def _rob(sub_nums):
            n = len(sub_nums)
            if n == 1:
                return sub_nums[0]
            if n == 0:
                return 0
            dp_0 = sub_nums[0] # 偷
            dp_1 = 0  # 不偷
            for i in range(1, n):
                p = sub_nums[i]
                dp_0, dp_1 = dp_1+p, max(dp_0, dp_1)
            return max(dp_1, dp_0)
        if len(nums) == 1:
            return nums[0]
        return max(_rob(nums[1:]), _rob(nums[:-1]))

提交结果2

打家劫舍Ⅲ

题目描述

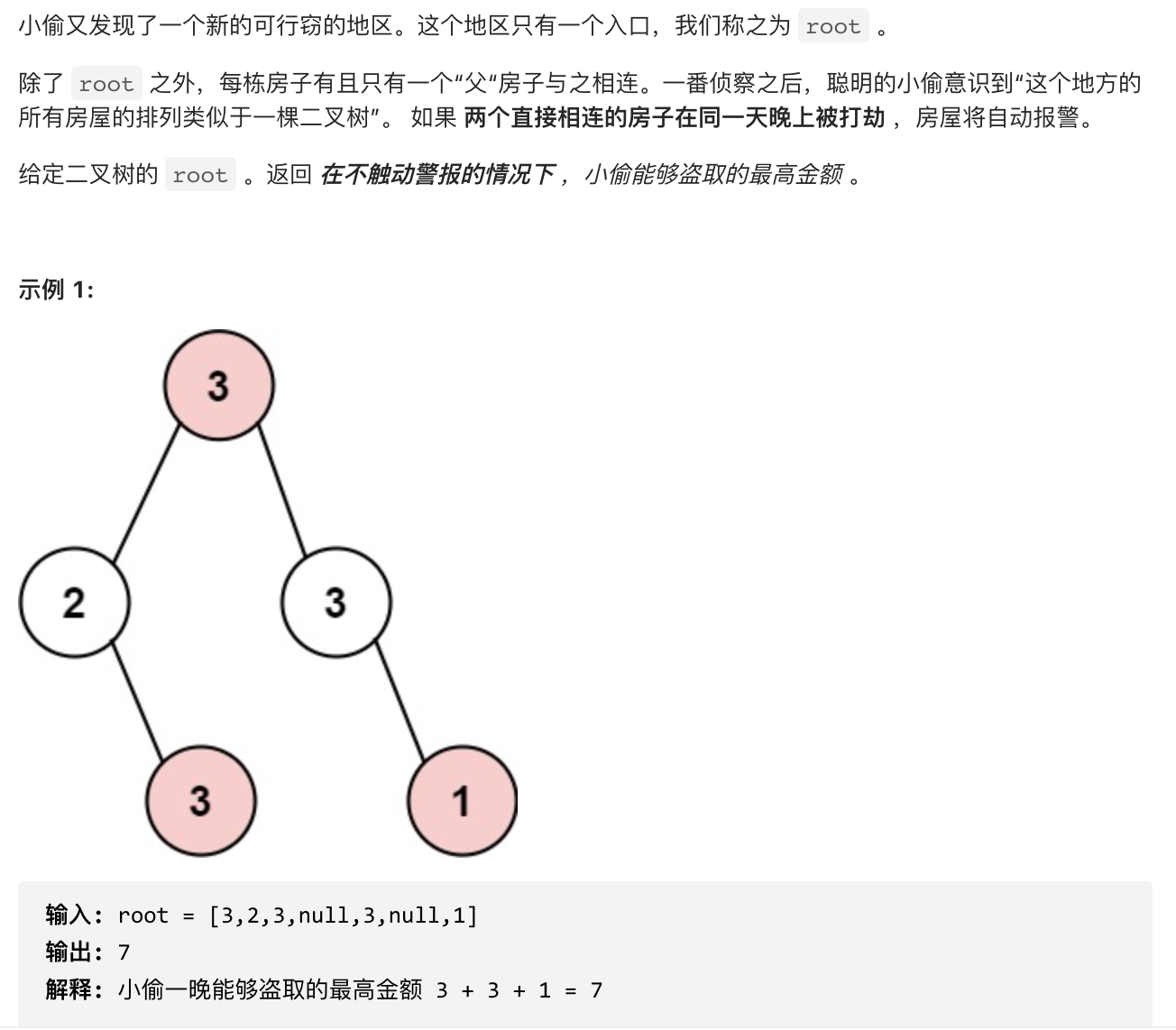
解题思路

房屋相连的方式已经变为树形结构了，看到这种结构想到树的遍历，所以使用自顶向下递归的方式是比较容易实现的。变量结果等式可以先列出：$dp(node)=not\_rob,is\_rob$，含义是当前节点为node时，返回偷当前node和不偷当前node时的最高金额。

状态转移方程为：

$$dp(node)=max(dp(node.left)) + max(dp(node.right)), \\ node.val + dp(node.left)[0] + dp(node.right)[0]$$

右边分为两个部分，就分别代表了$not\_rob$和$is\_rob$。

代码实现

class Solution:
    def rob(self, root: TreeNode) -> int:
        return max(self._rob(root))

    def _rob(self, node):
        if not node:
            return 0,0
        left = self._rob(node.left)
        right = self._rob(node.right)

        # 到每一个节点，都有偷或者不偷两种状态
        # 如果偷当前节点
        is_rob = node.val + left[0] + right[0]
        # 如果不偷当前节点
        not_rob = max(left) + max(right)
        return not_rob,is_rob

提交结果：