Haskell：`foldl`类型介绍

在编程语言中有一个叫做reduce 的函数，它可以应用于一些容器。它逐个元素，应用一个给定的二进制函数，并将当前的结果作为一个累加器保留，最后将累加器的值作为容器的摘要值返回。

例如，在Python中：

> reduce(lambda acc, elem: acc + elem, [1, 2, 3, 4, 5]) # sum of elements in a list
15

Haskell则有两个代表减少的基本函数，或者我们称之为折叠的函数--foldl 和foldr --它们在折叠的顺序上有所不同。foldl 从左到右减少容器中的元素（就像其他语言中的reduce 通常做的那样），而foldr 从右到左减少。

这两个函数是Foldable 类型类的核心方法，我们将在这篇文章中学习：

foldr 和 为一个列表foldl

首先，让我们弄清楚foldr 和foldl 对于一个列表是什么。

考虑一下下面的类型签名。

foldr :: (a -> b -> b) -> b -> [a] -> b
foldl :: (b -> a -> b) -> b -> [a] -> b

foldr

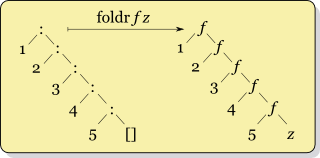
foldr 签名对应于从右到左折叠列表的函数。它把一个类型为a -> b -> b 的函数f 作为第一个参数，把一个类型为b 的初始（或基）值z 作为第二个参数，把一个类型为[a] 的列表xs = [x₁, x₂, ..., xₙ] 作为第三个参数。

让我们一步步地追踪它：

1. 引入一个累加器acc ，它在开始时等于z 。
2. f 应用于列表的最后一个元素 ( ) 和一个基本元素 ，其结果被写入累加器 - 。xₙ z xₙ `f` z
3. f 应用于列表中倒数第二的元素和累加器的当前值 - 。xₙ₋₁ `f` (xₙ `f` z)
4. 在经历了列表中的所有元素后，foldr ，将累加器作为一个摘要值返回，最后等于x₁ `f` (x₂ `f` ... (xₙ₋₁ `f` (xₙ `f` z)) ... ) 。

acc = z
acc = xₙ `f` z
acc = xₙ₋₁ `f` (xₙ `f` z)
...
acc = x₁ `f` (x₂ `f` ( ... (xₙ₋₁ `f` (xₙ `f` z)) ... )

这个过程可以用一幅图来表示：

foldl

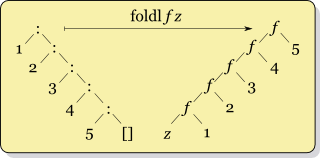
与foldr 不同，foldl 对一个列表进行从左到右的折叠。因此，f 首先应用于z 和x₁ -acc = z `f` x1 - 然后f 应用于累积器的当前值和x₂ -acc = (z `f` x₁) `f` x₂ - 以此类推。最后，foldl 返回acc = ( ... ((z `f` x₁) `f` x₂) `f` ... xₙ₋₁) `f` xₙ 。

acc = z
acc = z `f` x₁
acc = (z `f` x₁) `f` x₂
...
acc = ( ... (z `f` x₁) `f` x₂) `f` ...) `f` xₙ₋₁) `f` xₙ

这些操作的相应图示：

哈斯克尔定义

foldr 的递归Haskell定义如下：

instance Foldable [] where
  foldr :: (a -> b -> b) -> b -> [a] -> b
  foldr _ z []     =  z
  foldr f z (x:xs) =  x `f` foldr f z xs

foldl 是类似的；实现它是下面的练习之一。

简单的例子

让我们考虑几个简单的例子，将foldr 和foldl 应用于一个列表。

-- addition
ghci> foldr (+) 0 [1, 2, 3] -- 1 + (2 + (3 + 0))
6
ghci> foldl (+) 0 [1, 2, 3] -- ((0 + 1) + 2) + 3
6

-- exponentiation
ghci> foldr (^) 2 [2, 3] -- 2 ^ (3 ^ 2)
512
ghci> foldl (^) 2 [2, 3] -- (2 ^ 2) ^ 3
64

正如你所看到的，对于加法来说，从右到左或从左到右的折叠并不重要，因为其运算符是关联的。然而，当用指数运算符进行折叠时，顺序是重要的。

foldr 和的一般化foldl

幸运的是，我们不仅可以折叠列表！我们还可以实现 的实例。只要一个数据类型有一个类型参数，换句话说，当它的种类是* -> * ，我们就可以实现Foldable 的实例。

为了弄清Haskell数据类型的种类，你可以在GHCi中写:kind （或:k ）。要显示一个Haskell表达式的类型，可以使用:type （或:t ）。

例如，一个列表有一个类型参数--列表中元素的类型。

ghci> :kind []
[] :: * -> *

ghci> :type [1 :: Int, 2, 3]
[1, 2, 3] :: [Int]
ghci> :type ['a', 'b']
['a', 'b'] :: [Char]

Maybe a 数据类型也有一个类型参数--呈现值的类型。

ghci> :kind Maybe
Maybe :: * -> *

ghci> :type Just (2 :: Int)
Just 2 :: Maybe Int
ghci> :type Just "abc"
Just "abc" :: Maybe [Char]
ghci> :type Nothing
Nothing :: Maybe a -- can't decide what type `a` is

Int 和 String没有类型参数，而且你不能折叠它们。

ghci> :kind Int
Int :: *
ghci> :type (1 :: Int)
1 :: Int

ghci> :kind String
String :: *
ghci> :type ""
"" :: [Char]
ghci> :type "ab"
"ab" :: [Char]

Either a b 数据类型有两个类型参数，分别对应于 Left和Right 的值，所以也没有合理的方法来折叠一个 。但是我们可以定义 ，因为 Either a b 有一个合适的 instance Foldable (Either a) 类型。对于对数据类型 Either a * -> * instance Foldable ((,) a)也可以这样做。然而，这样的实例并不直观，因为它们只对类型参数中的一个进行操作。

ghci> :kind Either
Either :: * -> * -> *

ghci> :type Left (1 :: Int)
Left 1 :: Either Int b -- can't decide what type argument `b` is
ghci> :type Right 'a'
Right 'a' :: Either a Char -- can't decide what type argument `a` is

ghci> :kind Either Int
Either Int :: * -> *
ghci> :kind (,) Char
(,) Char :: * -> *

对于那些可以有一个Foldable 实例的数据类型，foldr 和foldl 的广义版本有以下类型签名。

foldr :: Foldable t => (a -> b -> b) -> b -> t a -> b
foldl :: Foldable t => (b -> a -> b) -> b -> t a -> b

以一些实例为例

Maybe a

让我们看一下Foldable 的其他实例。一个容易理解的例子是Maybe a'的实例。折叠Nothing ，返回一个基本元素，用foldr f z （或foldl f z ）还原Just x ，就是把f 应用到x 和z 。

instance Foldable Maybe where
  foldr :: (a -> b -> b) -> b -> Maybe a -> b
  foldr _ z Nothing  = z
  foldr f z (Just x) = f x z

使用实例：

ghci> foldr (+) 1 (Just 2)
3
ghci> foldr (+) 1 Nothing
1

BinarySearchTree a

可以为BinarySearchTree a 数据类型定义一个更有趣和可用的Foldable 实例。

考虑一个二进制搜索树，它的每个节点要么。

• 存储一个类型为a 的值，并且有左和右子树。
• 是一个没有值的叶子。

此外，对于每个非叶子节点n 。

• 其左子树中的所有值应小于或等于n's值。
• 而它的右子树中的所有值都应该大于n'的值。

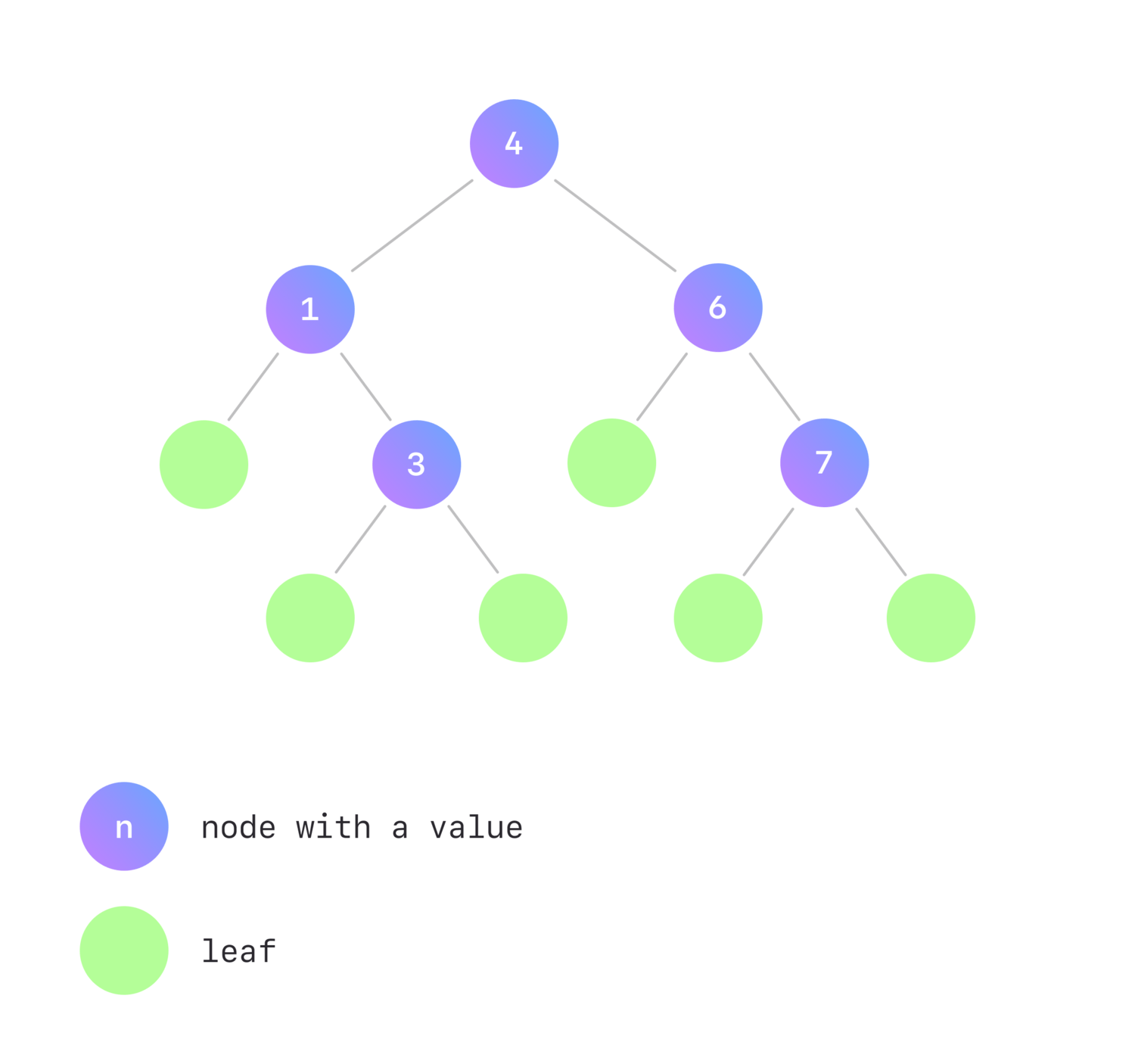
这个结构与下面的Haskell定义相匹配。

data BinarySearchTree a
  = Branch (BinarySearchTree a) a (BinarySearchTree a)
  | Leaf

想象一下，我们想把整个树减少到只有一个值。我们可以对节点的值进行求和，乘以它们，或者进行任何其他的二进制操作。所以，定义一个符合你目标的折叠函数是合理的。我们建议你尝试自己实现一个Foldable 实例；这是下面的练习之一。考虑到要定义foldr ，我们需要从右到左穿过树的元素--从右子树到左子树，通过连接它们的非叶子结点。

你需要什么来定义一个Foldable 实例？

为了回答这个问题，我们需要研究一下Foldable 的另一个方法，foldMap 。

foldMap

foldMap 有以下的声明：

foldMap :: (Monoid m, Foldable t) => (a -> m) -> t a -> m

值得注意的是，foldMap 有一个 Monoid约束。它的第一个参数是一个函数，用于将容器中的每个元素映射成一个单体，第二个参数是容器本身。在对元素进行映射后，使用(<>) 运算符对结果进行组合。折叠的顺序是从右到左，所以foldMap 可以通过foldr 来实现。

让我们来看看到底该怎么做：

foldMap :: (Monoid m, Foldable t) => (a -> m) -> t a -> m
foldMap f = foldr (\x acc -> f x <> acc) mempty

foldMap 没有一个基元素，因为只有容器的元素被减少。然而， 有，所以使用单体的身份-- ，是完全有意义的。我们还可以看到，折叠函数 是由 组成的，因此，当前的结果在每一步都被附加到一个单体累加器上。foldr mempty f (<>)

回顾一下列表元素如何用foldr 进行求和：

ghci> foldr (+) 0 [1, 2, 3]
6

为了在单体方面做同样的事情，考虑一个单体在加法下的情况 -- Sum.我们可以使用foldMap 和Sum 来执行列表元素的加法。

-- import `Data.Monoid` to get `Sum`
ghci> import Data.Monoid

ghci> foldMap Sum [1, 2, 3]
Sum {getSum = 6}

注意这里构造函数Sum 是一个将列表元素变成单数的函数。正如预期的那样，我们得到了同样的结果，它被包裹在Sum 中，可以很容易地通过getSum 访问。

总而言之，foldMap 和foldr 是可以互换的，区别在于前者从Monoid 实例中接收组合器和基元，而后者则明确地接受它们。

最小的完整定义

我们已经展示了foldMap 是如何使用foldr 来实现的。这并不明显，但foldr 也可以通过foldMap 来实现 !这是本文的题外话，因此，请继续在文档中了解细节。

因此，为了创建Foldable 实例，你可以提供一个foldr 或foldMap 的定义，这正是最小的完整定义 -foldMap | foldr 。注意，你不应该用foldr 来实现foldMap ，同时用foldMap 来实现foldr ，因为这只会永远循环。因此，你实现其中一个，Haskell会自动提供所有Foldable的方法的定义。

严格的foldl'

Haskell默认使用懒惰评估，在很多情况下，它可以对性能产生积极的影响。但懒惰有时也可能对其产生负面影响，折叠正是这种情况。

想象一下，你想对一个非常大的列表中的元素进行总结。当使用foldl 或foldr 时，累加器的值不会在每一步都被评估，所以一个thunk被累加。考虑到foldl ，在第一步，thunk 只是z `f` x₁ ，在第二步 -(z `f` x₁) `f` x₂ ，这不是什么大问题。但是在最后一步，累加器存储了( ... (z `f` x₁) `f` x₂) `f` ...) `f` xₙ₋₁) `f` xₙ 。如果列表的长度超过~10^8，thunk就会变得太大，无法存储在内存中，我们就会得到** Exception: stack overflow 。然而，这并不是放弃Haskell的原因，因为我们有foldl'!

foldl' 在每个步骤中执行弱头正常形式，从而防止thunk被累积。所以 ，通常是减少容器的理想方式，特别是当它很大的时候，你想要一个最终的严格结果。foldl'

这里有一些 "基准"，它们可能因计算机的特性而有所不同。但它们足以说明问题，以掌握严格折叠和懒惰折叠的性能差异。

-- set GHCi option to show time and memory consuming
ghci> :set +s

-- lazy `foldl` and `foldr`
ghci> foldl (+) 0 [1..10^7]
50000005000000
(1.97 secs, 1,612,359,432 bytes)

ghci> foldr (+) 0 [1..10^7] 
50000005000000
(1.50 secs, 1,615,360,800 bytes)

-- lazy `foldl` and `foldr`
ghci> foldl (+) 0 [1..10^8]
*** Exception: stack overflow

ghci> foldr (+) 0 [1..10^8]
*** Exception: stack overflow

-- strict `foldl'`
ghci> foldl' (+) 0 [1..10^8]
5000000050000000
(1.43 secs, 8,800,060,520 bytes)

ghci> foldl' (+) 0 [1..10^9]
500000000500000000
(15.28 secs, 88,000,061,896 bytes)

ghci> foldl' (+) 0 [1..10^10]
50000000005000000000
(263.51 secs, 1,139,609,364,240 bytes)

其他的方法有Foldable

foldl，foldr ，和foldMap ，可以说是理解Foldable 的本质的核心。尽管如此，还有其他一些方法值得一提。你可以通过定义foldr 或foldMap 来自动获得这些。

• length，你可能知道，它是通过foldl' 实现的。
• maximum 和 在它们的定义中使用严格的 。minimum foldMap'
• null，检查一个容器是否为空，也是通过减少后者的foldr 来实现的。
• 你可能会问，好的老的for 循环在哪里？幸运的是，Haskell也提供了它，如果没有Foldable ，这是不可能的。

总而言之，即使你很少使用foldr 和foldl 本身，你也会发现Foldable 的其他原语相当有用。你可以继续阅读文档以更好地了解它们。

练习

我们文章的理论部分已经结束。我们希望你现在知道什么是Foldable!我们建议你用我们的小练习来试试你的新知识。

1. 哪个定义是正确的？

   foldr (\s rest -> rest + length s) 0 ["aaa", "bbb", "s"]
   foldr (\rest s -> rest + length s) 0 ["aaa", "bbb", "s"]
   

   解答

   第一个定义是正确的。回顾一下foldr的第一个参数的类型签名--a -> b -> b 。a 类型在这里对应的是容器的类型，b 类型则是累加器的类型。在这个例子中，当前字符串的长度在每一步都被添加到累加器中，所以s 匹配当前元素，该元素具有容器的类型 -a 。

   ---

2. 递归地实现foldl 。

   提示：看一下上面的foldr 的定义。

   解决方案

   foldl :: (b -> a -> b) -> b -> [a] -> b
   foldl _ z []     =  z
   foldl f z (x:xs) =  foldl f (z `f` x) xs
   

   ---

3. 为BinarySearchTree a 实现foldr 。

   请记住，为了在实例定义中允许类型签名，你需要使用InstanceSigs 扩展。

   预期的行为：

   -- Binary search tree from the example picture above
   ghci> binarySearchTree = Branch (Branch Leaf 1 (Branch Leaf 3 Leaf)) 4 (Branch Leaf 6 (Branch Leaf 7 Leaf))
   
   ghci> foldr (+) 0 binarySearchTree
   21
   ghci> foldr (-) 0 binarySearchTree
   3
   ghci> foldl (-) 0 binarySearchTree
   -21
   

   解决方案

   instance Foldable BinarySearchTree where
     foldr :: (a -> b -> b) -> b -> BinarySearchTree a -> b
     foldr _ z Leaf                     = z
     foldr f z (Branch left node right) = foldr f (node `f` foldr f z right) left
   

   ---

4. 通过foldl ，为列表实现一个reverse 函数。

   预期的行为：

   ghci> reverse [1, 2, 3]
   [3, 2, 1]
   

   解决方案

   reverse :: [a] -> [a]
   reverse = foldl (\acc x -> x:acc) []
   

   ---

5. 通过foldr 为列表实现一个prefixes 函数。

   预期的行为：

   ghci> prefixes [1, 2, 3]
   [[1], [1, 2], [1, 2, 3]]
   
   ghci> prefixes []
   []
   

   解决方法

   prefixes :: [a] -> [[a]]
   prefixes = foldr (\x acc -> [x] : (map (x :) acc)) []
   

   ---

6. 通过foldr 和foldMap 实现二者的平方之和。

   预期的行为：

   ghci> sumSquares [1, 2, 3]
   14
   
   ghci> sumSquares []
   0
   

   用普通的方法解决foldr

   sumSquares :: [Int] -> Int
   sumSquares = foldr (\x acc -> x^2 + acc) 0
   

   ---

   用foldr 和 map来解决。

   sumSquares :: [Int] -> Int
   sumSquares xs = foldr (+) 0 (map (^2) xs)
   

   ---

   使用foldMap 和 getSum的解决方案。

   sumSquares :: [Int] -> Int
   sumSquares xs = getSum (foldMap (\x -> Sum x^2) xs)
   

   ---

谢谢您的阅读!