在这篇文章中,我将介绍反向模式自动微分(AD)的数学形式,并尝试解释反向模式AD的一些简单实现策略。其中包括Python和Rust的演示程序。
一个简单的例子
假设我们想计算一个表达式。
\z = x\cdot y + \sin(x)\] 。
要用程序来做这件事,我们就直接把它翻译成代码:
z = x * y + sin(x)
如果我们还对\(z\)的导数感兴趣呢?"显而易见 "的方法是用手(或用计算机代数系统)找到表达式,然后像以前那样把它打入计算机。但那是假设我们有一个明确的形式来表示 \(z\)。如果我们有的只是一个程序呢?
导致自动微分的重要认识是,即使是最大的、最复杂的程序也必须从一小部分原始操作(如加法、乘法或三角函数)中建立。链式规则使我们能够充分利用这一特性。
正向模式的自动微分
首先,我们需要思考计算机如何通过一连串的原始操作(乘法、正弦和加法)来评估\(z\):
# Program A
x = ?
y = ?
a = x * y
b = sin(x)
z = a + b
问号表示x 和y 是由用户提供的。
我很小心地避免了对同一变量的重新赋值:这样我们就可以把每个赋值当作一个普通的数学方程式。
\[\begin{align} x &= {?} \ y &= {?} a &= x cdot y \tag{A}.\\ b &= sin(x) z &= a + b end{align}\] 。
让我们试着对每个方程进行微分,相对于一些尚未给定的变量\(t\):
\[[begin{align} ]frac{partial x}{partial t} &= {?} tag{F1}]。\\ frac{partial y}{partial t} &= {?} `frac{partial a}{partial t} &= y `cdot `frac{partial x}{partial t}+ x `cdot+ x `cdot `frac{partial y}{partial t} `frac{partial y}{partial t}.\\ &= cos(x) cdot `frac{partial x}{partial t} `frac{partial x}{partial t}.\\ δfrac{partial z}{partial t} &= δfrac{partial a}{partial t}.+ frac{partial b}{partial t} end{align}\] 。
为了得到这个结果,我大量使用了链式规则:
\[\begin{align}\frac{partial w}{partial t} &= \sum_i \left(\frac{\partial w}{partial u_i} \cdot \frac{partial u_i}{partial t}\right) \tag{C1}\\ &= frac{partial w}{partial u_1}\cdot\frac{partial w}{partial u_1}.\cdot\frac{partial u_1}{partial t}。+ frac{partial w}{partial u_2}.\cdot (frac{partial u_2}{partial t})。+ \cdots end{align}\] 。
其中\(w\)表示某个输出变量,\(u_i\)表示\(w\)依赖的每个输入变量。
如果我们把\(t = x\) 代入方程(F1),我们就会有一个计算\(\部分 z / \部分 x\) 的算法。或者,为了得到\(\partial z / \partial y\),我们可以直接插入\(t = y\)来代替。
现在,让我们把方程(F1)翻译成涉及微分变量的普通程序{dx, dy, …} ,它们分别代表着\{partial x / \partial t, \partial y / \partial t, \ldots\}\)。
# Program B
dx = ?
dy = ?
da = y * dx + x * dy
db = cos(x) * dx
dz = da + db
如果我们把\(t = x\)替换到数学方程中,这个程序会发生什么?效果非常简单:我们只需要初始化dx = 1 和dy = 0 作为算法的种子值。因此,通过选择种子dx = 1 和dy = 0 ,在程序完成后,变量dz 将包含导数 \(\partial z / \partial x\)的值。同样,如果我们想要\(\partial z / \partial y\),我们会使用种子dx = 0 和dy = 1 ,变量dz 将包含\(\partial z / \partial y\) 的值。
到目前为止,我们已经展示了如何为一个特定的函数计算导数,比如我们的例子。为了使这一过程完全自动化,我们规定了一套规则,用于将一个评估表达式的程序(如程序A)翻译成评估其导数的程序(如程序B)。事实上,我们已经发现了其中的3条规则:
c = a + b => dc = da + db
c = a * b => dc = b * da + a * db
c = sin(a) => dc = cos(a) * da
这可以进一步扩展到减法、除法、幂、其他三角函数等,使用多变量微积分:
c = a - b => dc = da - db
c = a / b => dc = da / b - a * db / b ** 2
c = a ** b => dc = b * a ** (b - 1) * da + log(a) * a ** b * db
c = cos(a) => dc = -sin(a) * da
c = tan(a) => dc = da / cos(a) ** 2
为了使用这些规则进行翻译,我们只需将原始程序中的每个原始操作替换为其微分类似物。程序的顺序保持不变:如果一个语句K在另一个语句L之前被评估,那么语句K的微分类似物仍然在语句L的微分类似物之前被评估。
对程序A和程序B进行仔细检查后发现,实际上可以将微分计算与原始计算交错进行。
x = ?
dx = ?
y = ?
dy = ?
a = x * y
da = y * dx + x * dy
b = sin(x)
db = cos(x) * dx
z = a + b
dz = da + db
这显示了正向模式AD的两个主要优点:
- 微分变量通常取决于中间变量,所以如果我们把它们放在一起做,就不需要把中间变量保留到以后,这样可以节省内存。
- 这使得使用双数的实现成为可能。在有运算符重载的语言中,这可以转化为一个非常简单的、直接的正向模式AD的实现。
反向模式的自动分化
正向模式AD的实现简单,但也有一个很大的缺点,当我们想同时计算\(\partial z/partial x\)和\(\partial z/partial y\)时,这个缺点就很明显。在正向模式的AD中,这样做需要用dx = 1 和dy = 0 ,运行程序,然后用dx = 0 和dy = 1 ,再次运行程序。实际上,该方法的成本与O(n) ,其中n 是输入变量的数量成线性比例。如果我们想计算一个由许多变量组成的大型复杂函数的梯度,这将是非常昂贵的,这在实践中经常发生,令人惊讶。
让我们再看看我们用来推导正向模式AD的连锁规则(C1):
\begin{align}\frac{\partial w}{\partial t} &= \sum_i \left(\frac{\partial w}{partial u_i} \cdot \frac{partial u_i}{partial t}\right) \tag{C1}\\ &= frac{partial w}{partial u_1}\cdot\cdot\frac{partial u_1}{partial t}。+ frac{partial w}{partial u_2}.\cdot (frac{partial u_2}{partial t})。+ \cdots end{align}\] 。
为了用正向模式的AD计算梯度,我们必须进行两次替换:一次是用\(t = x\),另一次是用\(t = y\) 。这意味着我们必须将整个程序运行两次。
然而,连锁规则是对称的:它不关心 "分子 "或 "分母 "中的内容。所以让我们重写连锁规则,但把导数倒过来:
\\ &= rifrac{partial w_1}{partial u} cdot `frac{partial s}{partial w_1} `frac{partial s}{partial w_1}+ `frac{partial w_2}{partial u} `cdot `frac{partial s}{partial w_2}.+ \cdots end{align}\] 。
这样一来,我们就颠倒了变量的输入-输出角色。这里也使用了同样的命名规则。\`(u\)代表某个输入变量,`(w_i\)代表依赖于`(u\)的每个输出变量。尚未给出的变量现在被称为\(s\),以强调位置的变化。
在这种形式下,链式规则可以重复应用于每个输入变量\(u\),类似于在正向模式AD中我们重复应用链式规则于每个输出变量\(w\)以得到方程(F1)。因此,给定一些\(t\),我们希望使用链式规则(C2)的程序能够一次性计算出\(\partial s / \partial x\)和\(\partial s / \partial y\)!
到目前为止,这只是一种预感。让我们在例题(A)上试试吧:
\\ frac{partial s}{partial b} &= frac{partial s}{partial z}。\\ ﺔﻴﺋﺎﻄﻌﻟﺍ ﺾﻌﺑ ﺾﻌﺑ ﺾﻌﺑ\\ `frac{partial s}{partial y} &= x `cdot `frac{\partial s}{partial a} `frac{\partial s}{partial x} &= y `cdot `frac{\partial s}{partial a} + `cos(x) `cdot `frac{\partial s}{partial b} `end{align}\ ]
如果你以前没有做过,我建议花点时间用(C2)实际推导这些方程。这可能是相当令人费解的,因为一切看起来都是 "倒退 "的:我们不是问一个给定的输出变量取决于哪些输入变量,而是要问一个给定的输入变量可以影响哪些输出变量。最简单的方法是通过画表达式的依赖图来直观地看到这一点。
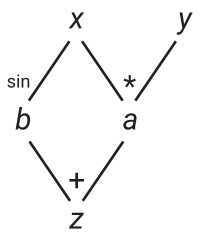
表达式的图形
该图显示
- 变量
a直接依赖于x和y。 - 变量
b直接依赖于x,并且 - 变量
z直接依赖于a和b。
或者,等价地。
- 变量
b可以直接影响z。 - 变量
a可以直接影响z。 - 变量
y可以直接影响到a,并且 - 变量
x可以直接影响a和b。
现在让我们把方程(R1)翻译成代码。和以前一样,我们用变量{gz, gb, …} ,即我们所说的邻接变量,来代替导数{{部分s/部分z,部分s/部分b,ldots\}}。这就导致了。
gz = ?
gb = gz
ga = gz
gy = x * ga
gx = y * ga + cos(x) * gb
回到方程(R1),我们看到,如果我们把\(s = z\)替换掉,我们将得到最后两个方程的梯度。在程序中,这相当于设置gz = 1 ,因为gz 只是\(\partial s / \partial z\)。我们不再需要运行两次程序了!这就是反向模式的自动区分。
当然,这也是一种折衷。如果我们想计算不同输出变量的导数,那么我们就必须用不同的种子重新运行程序,所以反向模式AD的成本是O(m) ,其中m 是输出变量的数量。如果我们有一个不同的例子,比如。
\z = 2 x + sin(x) v = 4 x + cos(x) end{cases}\] 。
在反向模式的AD中,我们必须用gz = 1 和gv = 0 (即\(s = z\))来运行程序,以获得\partial z / \partial x\),然后用gz = 0 和gv = 1 (即\(s = v\))重新运行程序,以获得\(\partial v / \partial x\)。相比之下,在正向模式的AD中,我们只需设置dx = 1 ,并在一次运行中得到\(\partial z / \partial x\) 和\(\partial v / \partial x\)。
然而,反向模式的AD有一个更微妙的问题:我们不能再把导数计算与原始表达式的评估交错进行,因为所有的导数计算似乎都是与原始程序相反的。此外,在使用一个简单的基于规则的算法时,如何到达这一点并不明显--运算符重载在这里甚至是一个有效的策略吗?我们如何将 "自动 "放回反向模式的AD中?
在Python中的一个简单实现
一种方法是解析原始程序,然后生成一个计算导数的邻接程序。这通常是相当复杂的实现,其难度也因宿主语言的复杂性而有很大不同。尽管如此,如果效率很高,这可能是值得的,因为在这种静态方法中,有更多的机会进行优化。
一个更简单的方法是动态地进行:在程序运行时构建一个完整的图来表示我们的原始表达。我们的目标是得到类似于我们之前绘制的依赖图的东西。

表达式的图
图的 "根 "是自变量x 和y ,这也可以看作是空操作。构建这些节点只是在堆上创建一个对象的简单问题。
class Var:
def __init__(self, value):
self.value = value
self.children = []
…
…
# define the Vars for the example problem
# initialize x = 0.5 and y = 4.2
x = Var(0.5)
y = Var(4.2)
每个Var 节点存储什么?每个节点可以有几个子节点,也就是直接依赖该节点的其他节点。在这个例子中,x ,它的子节点是a 和b 。这个图中不允许有循环。
默认情况下,一个节点被创建时没有任何子节点。然而,每当一个新的表达式(u\)从现有的节点(w_i\)中建立起来时,新的表达式(u\)会将自己注册为它的每个依赖节点(w_i\)的子节点。在注册子节点的过程中,它也会保存其贡献权重
\[\frac{partial w_i}{partial u}\] 。
这将在以后用于计算梯度。作为一个例子,这里是我们如何做乘法的。
class Var:
…
def __mul__(self, other):
z = Var(self.value * other.value)
self.children.append((other.value, z)) # weight = ∂z/∂self = other.value
other.children.append((self.value, z)) # weight = ∂z/∂other = self.value
return z
…
…
# “a” is a new Var that is a child of both x and y
a = x * y
正如你所看到的,这个方法,就像大多数反向模式AD的动态方法一样,需要在引擎盖下进行大量的突变。
最后,为了得到导数,我们需要对导数进行传播。这可以通过递归来完成,从根x 和y 。为了避免不必要地多次遍历树,我们在一个叫做grad_value 的属性中缓存了值。
class Var:
def __init__(self):
…
# initialize to None, which means it’s not yet evaluated
self.grad_value = None
def grad(self):
# recurse only if the value is not yet cached
if self.grad_value is None:
# calculate derivative using chain rule
self.grad_value = sum(weight * var.grad()
for weight, var in self.children)
return self.grad_value
…
…
a.grad_value = 1.0
print("∂a/∂x = {}".format(x.grad())) # ∂a/∂x = 4.2
下面是这个方法在Python中的完整演示。
请注意,由于我们正在突变节点的grad_value 属性,我们不能重用树来计算不同输出变量的导数,除非遍历整个树并将每个grad_value 属性重置为None 。
Rust中基于磁带的实现
所描述的方法不是很有效:一个复杂的表达式可能包含大量的原始操作,导致大量的节点被分配到堆上。
一个更节省空间的方法是通过将节点追加到一个现有的、可增长的数组中来创建节点。然后,我们就可以通过这个可增长数组中的索引来引用每个节点。请注意,我们在这里不使用指针。如果向量的容量发生变化,指向其元素的指针将变得无效。
使用向量来存储节点在减少分配数量方面做得很好,但是,像任何竞技场的分配方法一样,我们将不能取消图的部分分配。这是全或无。
另外,我们需要以某种方式将每个节点放入一个固定的空间。但是,我们将如何存储它的子节点列表呢?
事实证明,我们实际上不需要存储子节点。相反,每个节点可以只存储其父节点的索引。从概念上讲,对于我们的例子问题,它看起来像这样。

图的具体表示
注意与前面的图的相似性。
在Rust中,我们可以用一个包含两个权重和两个父节点索引的结构来描述每个节点。
struct Node {
weights: [f64; 2],
deps: [usize; 2], // parent (“dependency”) indices
}
你可能想知道为什么我们选择了两个。这是因为我们假设所有的原始操作都是二进制的。例如,变量a = x * y 的节点会看起来像。
Node {
weights: [
y.value, // ∂a/∂x
x.value, // ∂a/∂y
],
deps: [x.index, y.index],
}
但也有单数和空数操作--我们将如何处理这些操作?其实很简单,我们只需将权重设为零。例如,变量b = sin(x) 的节点将看起来像。
Node {
weights: [
x.value.cos(), // ∂b/∂x
0.0,
]
deps: [x.index, /* whatever */],
}
作为一个惯例,我们将把节点本身的索引放入/* whatever */ 。只要索引不出界,我们在里面放什么真的不重要。
节点本身被存储在一个公共数组(Vec<Node> )中,这个数组被整个表达式图所共享,它也充当了分配区。在AD文献中,这个共享数组通常被称为磁带(或Wengert列表)。磁带可以被认为是表达式评估过程中所有操作的记录,反过来,它又包含了反向读取时计算其梯度所需的所有信息。
在Python的实现中,节点是用表达式来识别的:节点可以直接通过算术运算来组合成新的节点。在Rust中,我们将节点和表达式视为独立的实体。节点只存在于磁带上,而表达式只是对节点索引的薄薄包装。下面是表达式类型的样子。
#[derive(Clone, Copy)]
pub struct Var<'t> {
tape: &'t Tape,
index: usize,
value: f64,
}
表达式类型包含一个指向磁带的指针,一个指向节点的索引,以及一个相关的值。请注意,表达式满足Copy ,这使得它可以不顾一切地自由复制。这对于保持表达式像普通浮点数一样行动的假象是必要的。
另外,请注意,磁带是一个不可变的指针。我们需要在建立表达式时修改磁带,但是我们会有很多表达式持有指向同一个磁带的指针。这在可变指针上是行不通的,因为它们是排他的,所以我们必须使用RefCell"欺骗 "Rust的读写锁系统。
pub struct Tape { nodes: RefCell<Vec<Node>> }
大部分的实现工作在于对原始操作进行编码。下面是单选sin 函数的样子。
impl<'t> Var<'t> {
pub fn sin(self) -> Self {
Var {
tape: self.tape,
value: self.value.sin(),
index: self.tape.push1(
self.index, self.value.cos(),
),
}
}
}
任何一元函数都可以像这样实现。在这里,push1 是一个辅助函数,它构造了节点,把它推到磁带上,然后返回这个新节点的索引。
impl Tape {
fn push1(&self, dep0: usize, weight0: f64) -> usize {
let mut nodes = self.nodes.borrow_mut();
let len = nodes.len();
nodes.push(Node {
weights: [weight0, 0.0],
deps: [dep0, len],
});
len
}
}
最后,当需要进行导数计算时,我们需要反向遍历整个磁带,并使用链规则累积导数。这是由与Var 对象相关的grad 函数完成的。
impl<'t> Var<'t> {
pub fn grad(&self) -> Grad {
let len = self.tape.len();
let nodes = self.tape.nodes.borrow();
// allocate the array of derivatives (specifically: adjoints)
let mut derivs = vec![0.0; len];
// seed
derivs[self.index] = 1.0;
// traverse the tape in reverse
for i in (0 .. len).rev() {
let node = nodes[i];
let deriv = derivs[i];
// update the adjoints for its parent nodes
for j in 0 .. 2 {
derivs[node.deps[j]] += node.weights[j] * deriv;
}
}
Grad { derivs: derivs }
}
}
关键部分在于循环。在这里,我们没有像链式规则(C2)或Python程序那样同时对所有导数进行求和。相反,我们将连锁规则分解为一连串的加法分配。
\[\frac{\partial s}{\partial u} \leftarrow \frac{\partial s}{partial u} + \frac{\partial w_i}{partial u} \frac{\partial s}{partial w_i}\] 。
我们这样做的原因是,我们不再记录孩子的情况。因此,我们不是一下子积累每个孩子贡献的所有导数,而是让每个节点以自己的速度对它们的父母做出贡献。
与Python程序的另一个主要区别是,现在导数被存储在一个单独的数组derivs ,然后被伪装成一个Grad 对象。
pub struct Grad { derivs: Vec<f64> }
这意味着,与Python程序不同的是,所有的导数都存储在每个节点的grad_value 属性中,我们已经将磁带与导数的存储解耦,允许磁带/表达式图被重新用于多个反向模式的AD计算(如果我们有多个输出变量的话)。
derivs 数组包含与其相关节点相同索引的所有邻接/导数。因此,要获得一个节点位于索引3 的变量的邻接,我们只需要抓取索引derivs 数组中的元素3 。这是由Grad 对象的wrt ("with respect to")函数实现的。
impl Grad {
pub fn wrt<'t>(&self, var: Var<'t>) -> f64 {
self.derivs[var.index]
}
}
下面是Rust中反向模式AD的完整演示。要使用这个初级的AD库,你要写。
let t = Tape::new();
let x = t.var(0.5);
let y = t.var(4.2);
let z = x * y + x.sin();
let grad = z.grad();
println!("z = {}", z.value); // z = 2.579425538604203
println!("∂z/∂x = {}", grad.wrt(x)); // ∂z/∂x = 5.077582561890373
println!("∂z/∂y = {}", grad.wrt(y)); // ∂z/∂y = 0.5
总微分和微分算子
请注意,如果我们把方程(F1)的分母中的\(\partial t\)扔掉,我们最终会得到一组与每个变量的总差值有关的方程。
\begin{align} \mathrm{d} x &= {? } \mathrm{d} y &= {?} \mathrm{d} a &= y \cdot \mathrm{d} x + x \cdot \mathrm{d} y \mathrm{d} b &= cos(x) \cdot \mathrm{d} x \mathrm{d} z &= \mathrm{d} a + \mathrm{d} b END{align}\ ]
这就是为什么像dx 这样的变量被称为 "差值"。我们也可以用类似的形式写出连锁规则(C1)。
\w = sum_i \left(\frac{\partial w}{partial u_i} \cdot \mathrm{d} u_i\right)\] 。
同样,我们可以抛开方程(R1)中的\(s\),然后变成一个微分算子的方程。
\[\begin{align} \frac{\partial}{\partial z} &= {?} \frac{\partial}{\partial b} &= \frac{\partial}{\partial z}.\\ Frac{partial}{partial a} &= `frac{partial}{partial z}。\\ `frac{partial}{partial y} &= x `cdot `frac{partial}{partial a} `frac{partial}{partial x} &= y `cdot `frac{partial}{partial a} + `cos(x) `cdot `frac{partial}{partial b} `end{align}\ ]
我们可以对(C2)做同样的处理。
\tag{C4}\" [\frac{partial}{\partial u} = \sum_i \left(\frac{partial w_i}{partial u} \cdot \frac{\partial}{partial w_i}\right)
通过基于CTZ的策略节省内存
好吧,这一节并不是教程的一部分,而是关于一个特殊的优化策略的讨论,我觉得这个策略很有趣,值得详细说明一下(它在Griewank的一篇论文中得到了简要的解释)。
到目前为止,我们已经接受了这样一个事实,即反向模式的AD需要与中间变量数量成比例的存储。
然而,这并不完全正确。如果我们愿意重复一些中间计算,我们可以用更少的存储空间来完成。
假设我们有一个表达式图,它或多或少是一条从输入到输出的直线,中间有N 个中介变量。所以这已经不是一个表达式图了,而是一个链。在天真的解决方案中,我们需要为这个很长的表达式链提供O(N) 存储空间。
现在,我们不再缓存所有的中间变量,而是构建了一个缓存的层次结构,并在整个反向扫描过程中保持这个层次结构。
cache_0存储初始值cache_1储存链上一半的结果cache_2储存链上3/4的结果cache_3储存链上7/8处的结果cache_4存储链上15/16处的结果- ...
请注意,存储需求被降低到O(log(N)) ,因为我们的缓存值永远不会超过log2(N) + 1 。
在前向扫描过程中,维护这样一个层次结构需要在一个由count-trailing-zeros函数决定的索引处驱逐旧的缓存条目。
要理解基于CTZ的策略,最简单的方法是看一个例子。假设我们有一个16个操作的链,其中0 是初始输入,f 是最终输出。
0 1 2 3 4 5 6 7 8 9 a b c d e f
假设我们已经完成了从0 到f 的前向扫描。在此过程中,我们已经缓存了0 、8 、c 、e 和f 。
0 1 2 3 4 5 6 7 8 9 a b c d e f
^
X---------------X-------X---X-X
X 符号表示结果已被缓存,而^ 表示我们反向扫描的状态。现在让我们开始向后移动。e 和f 都是可用的,所以我们可以顺利地移过e 。
0 1 2 3 4 5 6 7 8 9 a b c d e f
^
X---------------X-------X---X-X
现在我们遇到了第一个问题:我们缺少d 。所以我们从c ,重新计算d 。
0 1 2 3 4 5 6 7 8 9 a b c d e f
^
X---------------X-------X---X-X
|
+-X
然后我们继续前进,经过c 。
0 1 2 3 4 5 6 7 8 9 a b c d e f
^
X---------------X-------X---X-X
|
+-X
现在我们缺少了b 。所以我们从8 开始重新计算,但在这样做的时候我们也缓存了a 。
0 1 2 3 4 5 6 7 8 9 a b c d e f
^
X---------------X-------X---X-X
| |
+---X-X +-X
我们继续前进,经过a 。
0 1 2 3 4 5 6 7 8 9 a b c d e f
^
X---------------X-------X---X-X
| |
+---X-X +-X
现在缺少了9 ,所以从8 重新计算。
0 1 2 3 4 5 6 7 8 9 a b c d e f
^
X---------------X-------X---X-X
| |
+---X-X +-X
|
+-X
然后我们移过8 。
0 1 2 3 4 5 6 7 8 9 a b c d e f
^
X---------------X-------X---X-X
| |
+---X-X +-X
|
+-X
为了得到7 ,我们从0 开始重新计算,但在这样做的时候,我们也保留了4 和6 。
0 1 2 3 4 5 6 7 8 9 a b c d e f
^
X---------------X-------X---X-X
| | |
+-------X---X-X +---X-X +-X
|
+-X
现在你可能已经看到了这个模式。下面是接下来的几个步骤。
0 1 2 3 4 5 6 7 8 9 a b c d e f
^
X---------------X-------X---X-X
| | |
+-------X---X-X +---X-X +-X
| |
+-X +-X
0 1 2 3 4 5 6 7 8 9 a b c d e f
^
X---------------X-------X---X-X
| | |
+-------X---X-X +---X-X +-X
| |
+-X +-X
0 1 2 3 4 5 6 7 8 9 a b c d e f
^
X---------------X-------X---X-X
| | |
+-------X---X-X +---X-X +-X
| | |
+---X-X +-X +-X
0 1 2 3 4 5 6 7 8 9 a b c d e f
^
X---------------X-------X---X-X
| | |
+-------X---X-X +---X-X +-X
| | |
+---X-X +-X +-X
0 1 2 3 4 5 6 7 8 9 a b c d e f
^
X---------------X-------X---X-X
| | |
+-------X---X-X +---X-X +-X
| | |
+---X-X +-X +-X
|
+-X
0 1 2 3 4 5 6 7 8 9 a b c d e f
^
X---------------X-------X---X-X
| | |
+-------X---X-X +---X-X +-X
| | |
+---X-X +-X +-X
|
+-X
从这里可以看出,重复计算的次数是由O(log(N)) ,因为上面的图只是扁平化的二叉树,其高度是有对数限制的。
下面是一个基于CTZ的链式策略的演示。
正如Griewank所指出的,这个策略并不是最理想的策略,但它的优点是实现起来相当简单,特别是当计算步骤的数量不预先知道时。在他的论文中还有其他一些策略,你可能会觉得很有趣。