随机过程及其在机器学习中的应用指南许多物理和工程系统使用随机过程作为建模和推理的关键工具。随机过程是一个概率模型，描述

许多物理和工程系统使用随机过程作为建模和推理的关键工具。随机过程是一个概率模型，描述了代表可能的样本路径的时间有序的随机变量的集合。它被广泛用作系统和现象的数学模型，这些系统和现象似乎以随机的方式变化。作为统计学的一项经典技术，随机过程被广泛用于各种领域，包括生物信息学、神经科学、图像处理、金融市场等。在这篇文章中，我们将详细讨论随机过程，并试图了解它与机器学习的关系以及它的主要应用领域是什么。本文要讨论的主要内容概述如下。

随机性的一般意义

随机性是指被随机概率分布很好地描述的特性。虽然随机性和随机性是不同的，前者指的是一种建模方法，后者指的是现象，但这两个术语经常被互换使用。此外，随机过程的正式概念也被称为概率论中的随机过程。

随机性被应用于各种领域，包括生物学、化学、生态学、神经科学和物理学，以及图像处理、信号处理、信息理论、计算机科学、密码学和电信。它也被运用于健康、语言学、音乐、媒体、色彩理论、植物学、制造业和地貌学，所有这些都受到金融市场中看似随机的运动的影响。在社会科学中，利用了随机建模。

随机过程

尽管随机过程的定义各不相同，但它通常被描述为由某个集合索引的随机变量的集合。在没有明确描述索引集的情况下，随机过程和随机过程这两个短语被认为是同义词，可以互换使用。短语 "集合 "和 "族 "可以互换使用，而 "参数集 "或 "参数空间 "偶尔也被用来代替 "索引集"。

一些理论上定义的随机过程包括随机漫步、马汀格、马尔可夫过程、莱维过程、高斯过程、随机场、更新过程和分支过程。概率论、微积分、线性代数、集合论和拓扑学，以及实分析、度量论、傅里叶分析和函数分析，都被用于研究随机过程。

随机过程的例子

泊松过程

泊松过程是一个具有多个定义和应用的随机过程。它是一个计数过程，是一个随机过程，在这个过程中，随着时间的推移，会显示出随机数量的点或发生。一个随时间变化的泊松随机变量被定义为一个过程中在零和某一时间之间的点的数量。非负数构成了这个过程的索引集，但自然数构成了状态空间。因为它可以被设想为一种计数操作，所以这个过程通常被称为泊松计数过程。

伯努利过程

最基本的随机过程之一是伯努利过程。它是一组独立和相同分布（iid）的随机变量，每个变量的概率为1或0，例如，1的概率为p，0的概率为1-p。这种方法类似于反复投掷硬币，得到头的概率为p，数值为1，得到尾的概率为0。换句话说，伯努利过程是一组iid伯努利随机变量，每次抛硬币代表一次伯努利试验。

随机漫步

简单的随机漫步是随机漫步的一个典型例子。它是一个以整数为状态空间的离散时间的随机过程，以伯努利过程为基础，每个伯努利变量要么取正值，要么取负值。换句话说，简单的随机漫步发生在整数上，其数值以概率p增长1，或以概率1-p降低1，因此这种随机漫步的索引集是自然数，但其状态空间是整数。如果p=0.5，这种随机行走被称为对称随机行走。

将随机系统与其他系统进行比较

让我们把随机系统与其他偶尔被用作随机的同义词的类似术语进行比较，以便更好地掌握它。随机是随机和概率的同义词，尽管非决定性与随机有区别。

随机性与梯度

随机性与概率性

随机性和概率性这两个词经常被互换。概率性很可能是更广泛的术语。随机性取决于以前发生的情况，比如股票价格的波动是基于前一天的价格，但概率性是独立于其他观察的，比如中奖号码，它们应该是相互独立的。

随机性与非决定性

确定性指的是一个变量或过程可以根据当前情况预测发生的结果。简单地说，我们可以说明，在决定论的模型中没有任何东西是随机的。另一方面，非决定性是指一个变量或过程，同样的输入可能导致不同的结果。

因为结果是不可预测的，所以随机性经常与非决定性的方法交替使用。在我们可能使用预期结果和方差等概率工具进行分析时，随机性与非决定性略有不同。因此，将一个变量定义为随机性而不是非决定性是一个更有力的主张。

随机性 Vs 随机性

在大多数情况下，随机性与随机性是可以互换使用的。随机指的是不可预测，在理想的情况下，所有的结果都是同样可能的，意味着不依赖其他的观察，比如抛出一个公平的硬币，而随机指的是随机选择的变量的概率性质。

机器学习中的随机过程

随机性被用来解释几个机器学习方法和模型。这是由于许多优化和学习算法必须在随机领域发挥作用，而且一些算法依赖于随机性或概率性决定。让我们更详细地看看机器学习中不确定性的来源和随机算法的性质。

在机器学习中是如何识别的

涉及不确定性的领域被称为随机性。统计噪音或随机错误会导致目标或目标函数的不确定性。也可能是由于用于拟合模型的数据是更大群体的一个样本。最后，所采用的模型很少能够捕捉到领域的所有元素，而是必须概括到未知的情况，从而导致保真度的损失。

优化随机的

创建和采用随机变量的优化方法被称为随机优化（SO）。随机变量存在于随机问题的优化问题本身的表述中，它包含了随机目标函数或随机约束。随机迭代方法也包括在随机优化方法中。一些随机优化方法结合了随机优化的两个定义，使用随机迭代来解决随机问题。

以下是随机优化算法的一些实例：

粒子群优化
模拟退火
遗传算法

随机学习算法

机器学习中最普遍和广泛使用的两种算法是随机梯度下降和随机梯度提升。

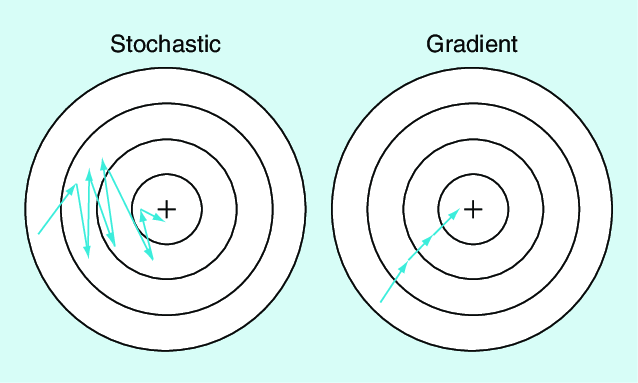
随机梯度下降（SGD）是梯度下降技术的一个变种，它为训练数据集中的每个例子计算误差并更新模型。由于模型是为每个训练实例更新的，随机梯度下降经常被称为在线机器学习算法。

随机梯度提升算法是决策树技术的集合。随机方面指的是从训练数据集中抽取的随机行子集，利用它来建立树，特别是树的分裂点。

随机过程的应用

随机模型被用于金融市场，以反映资产的看似随机的行为，如股票、商品、相对货币价值（即一种货币相对于另一种货币的价格，如美元相对于欧元的价格）和利率。
制造程序被认为是随机的。这个假设对批量和连续的制造过程都是正确的。过程控制图描绘了一个跨时间的特定过程控制参数，用于记录过程的测试和监测。
观众口味和偏好的营销和转移，以及某些电影和电视首映的招徕和科学的吸引力（即开幕周末、口碑、被调查群体中的首要知识、明星名字的认可，以及社会媒体宣传和广告的其他元素），都部分地受到随机模型的影响。
Stanislaw Ulam和Nicholas Metropolis推广了蒙特卡洛方法，这是一种随机方法。随机性的使用和程序的重复性让人想起了赌场活动。仿真和统计抽样方法通常被用来测试一个先前理解的确定性问题，而不是反过来。尽管历史上存在 "倒置 "技术的例子，但在蒙特卡洛方法得到普及之前，它们并没有被视为一种通用策略。

结论

在这篇文章中，我们用不同的概念和应用领域来理解随机过程。我们在这篇文章中经历了随机的定义，它与随机、概率、非确定性等相关术语的区别，以及随机在机器学习中的意义。此外，我们还有一些基本的和常见的随机过程的例子，这些例子可以在通用术语中看到。

随机过程及其在机器学习中的应用指南

目录