对 "无限 "有不同的定义,这取决于它们在不同框架和领域中的使用方式。我们强调的是在数学和计算机科学中利用的内容。无限可以定义为许多比实数大的 "不确定"。
既有正无穷,也有负无穷,因为它存在于数线的起点和终点。它可以被定义为 "不确定的程序 "的结果,如任何数字除以0。在编程中,它被利用来说明整个最大或最小的标准,在程序中与众不同的优化。例如,检测图中两个节点之间的直接路径的程序可以将直接路径距离的原始评估设定为无穷大。
如果指数部分的每一位都是1,尾数部分的每一位都是0,那么浮点数字就表示为无穷大。另外,当0为符号位时,它显示的是正无穷大,如果符号位是1,它就是负无穷大。无穷大是一个独特的数字,简单的二进制描述无法表示,所以浮点数是它在python中的数据类型。在这篇文章中,我们将讨论更多的无穷大。
声明无穷大
有一些方法可以在Python中表达无穷大。让我们看一下其中的一些。我们通过将系数为`inf`或`infinity`的字符串声明为float模式来断言无穷大是一个数据类型float。
还有一个 "负无穷大",我们可以通过声明'-inf'或使其成为正无穷大,然后在其前面加上'-'号来断言。
传递给float模式的字符串是不区分大小写的。传递的 "INF "或 "inFINIty "也被正确地估价为inf。我们还利用Python的数学模式来象征无穷大。该段包含预定义的数字math.inf,它被分配到一个标志着无穷大的变量。

在这种情况下,我们取两个无穷大。一个由'c'变量表示的无限是正数,另一个由'd'表示的无限是负数。

为了运行这段代码,我们在键盘上按下了F5。打印值打印出c和d的值,也打印出c的数据类型。
关于无穷大的加法
由于无穷大是一个浮动的数字,我们对它进行了各种算术处理。当我们在一个有限实数和无穷大之间做加法时,结果是无穷大。当我们将一个无穷大的数字与其他无穷大的数字做加法时,结果又是无穷大。但是,当我们做一个负的无穷大数与正的无穷大数之间的加法时,其结果是不确定的或NaN(不是一个数字)。

在这个例子中,NaN是一个不同的数字,类似于无穷大,在Python中被表示为数据类型float。这段代码显示了一个无穷大的数字与任何浮点数、与任何整数、与其他整数,以及与具有相反符号的数字相加的结果。

无限大的最大值
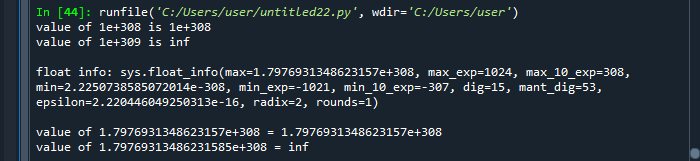
我们已经解释过,无穷大是一个 "不确定的数字",大于任何有限的数量。然而,计算机对一个变量可能保存的极端值有一个限制。我们不会赋予它极大的价值,并将其与无穷大联系起来。在Python中,这里我们使用1e + 308和1e + 309之间的值。这是由浮动变量保存的最高值。特定的值可以通过利用'sys.float_info'参数来确定。

它显示了数据类型float在这个例子中的几个占有率,比如说由浮点变量保存的最高值。大于这个数字的值被推断为无穷大。同样,小于一个确定的最小数的数字被推断为负数的无穷大。
NumPy的无穷大
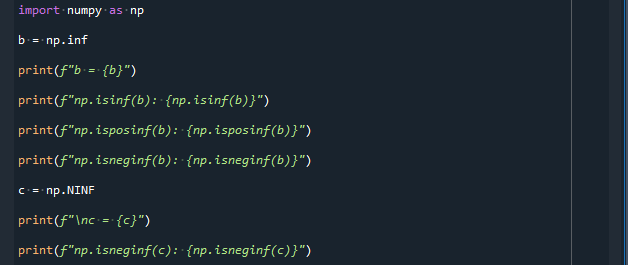
就像数学模块,float方法一样,我们也可以利用np.inf系数来分配无穷大。NumPy遵从IEEE 754惯例保存浮点数;因此,np.inf的数字等同于float("inf")和math.inf。我们利用np.inf的数据类型float。
我们也可以通过多个假名来访问NumPy的无穷大系数,例如,np.Infinity、np.Inf和np.infty。NumPy还陈述了正负无限的孤立数字。正的永恒可以通过np.pinf(也称为np.inf)来检索,而我们使用系数np.ninf来访问负的无限。NumPy还包含一个技术来检查数字是否是无限的。也有一种独特的方法来查找数字是否为正数或数字是否为负无穷大。我们可以向这些方法传递一个NumPy的组合。给出一个布尔数字的数组,表示无限值数组中的一个位置。
模式数学也包含isinf技术,但没有检查正负无限的程序。另一方面,NumPy包含一个叫做np.isinf的技术,可以发现数字是否是有限的。在对变量'b'和'c'施加不同条件后,我们通过运行这段代码看到了结果。

总结
在计算机科学中,对无限的利用是非常好的。一般来说,当我们将数字与大数字或非常小的数字进行比较时,我们会利用无限大。此外,它还被利用到制定各种算法的程度。这通常被用于广泛的计算。