布隆过滤器(Bloom Filter)，是由Howard Bloom在1970年提出的二进制向量数据结构，具有很好的空间和时间效率，尤其是空间效率极高，BF常常被用来检测某个元素是否是巨量数据集合中的成员。

基本原理

BF可以高效地表征集合数据，其使用长度为m的位数组来存储集合信息，同时使用k个相互独立的哈希函数将数据映射到位数组空间。

其基本思想如下：首先，将长度为m的位数组元素全部置为0。对于集合S中的某个成员a，分别使用k个哈希函数对其计算，如果 $h_i(a)=x, (1 \le i \le k, 1 \le x \le m)$ ，将位数组的第x位置为1，对于成员a来说，经过k个哈希函数计算后，可能会将位数组中的 $w(w \le k)$ 位为1。对于集合中的其他成员也如此处理，这样即可完成位数组空间的集合表示。其算法流程如下：

BloomFilter(set A, hash_functions, integer m)
	filter[1...m]= 0;   //大小为m的位数组初始化为0
 	foreach ai xin A:
 		foreach hash function hj:
 			filter[hj(ai)] = 1;
 		end foreach
	end foreach
	return filter

当查询某个成员a是否在集合S中出现时，使用相同的k个哈希函数计算，如果其对应位数组中的w位( $w \le k$ )都为1，则判断成员a 属于集合S，只要w位中有任意一位为0，则判断成员a不属于集合S，其算法流程如下：

 MembershipTest(element, filter, hash_functions)
 	foreach hash function hj:
 		if filter[hj(element)] != 1 then
 			return False
 		end foreach
	return True

在查询某个成员是否属于集合时，会发生误判（False Positive）。也就是说，如果某个成员不在集合中，有可能BF会得出其在集合中的结论。但是不会发生漏判（False Negative）的情况，即如果某个成员确实属于集合，那么BF一定能够给出正确判断。

误判率计算

集合大小n、哈希函数的个数k和位数组大小m会影响误判率,对其关系进行推导:

\begin{array}{l} 某元素由Hash函数插入时相应位置不为1的概率为: 1-\frac{1}{m}\\ 经过k个Hash函数，该位置仍然没有被置为1的概率为: (1-\frac{1}{m})^k\\ 那么插入n个元素，该位置仍未被置为1的概率为: (1-\frac{1}{m})^{kn}\\ 该位置被置为1的概率为：1 - (1-\frac{1}{m})^{kn} \\ 在检测某个元素是否存在于集合中时，误判时会认为相应位置所有的Hash值对应的位置的值都是1，误判的概率\left[1 - (1-\frac{1}{m})^{kn} \right ]^k \\ 由于\lim_{x \to 0} (1+\frac{1}{x})^{x} = e\\ \Rightarrow \left[1 - (1-\frac{1}{m})^{kn} \right ]^k = \left[1 - (1-\frac{1}{m})^{-m * -\frac{kn}{m}} \right ]^k \approx (1-e^{-\frac{kn}{m}})^k \\ \\ \\ 假设给定m和n，计算k为什么值时误判率最低？\\ 对于误判函数f(k) = (1-e^{-\frac{kn}{m}})^k \\ 记b = e^{(\frac{n}{m})},则f(k) = (1-b^{-k})^k \\ 两边去对数则, ln[f(k)] = k * ln(1-b^{-k}),对其求导得 \\ \frac{1}{f(k)}*{f}'(k) = ln(1-b^{-k}) + k * \frac{1}{1-b^{-k}} * (-b^{-k}) * lnb * (-1) \\ = ln(1-b^{-k}) + k * \frac{b^{-k} * lnb}{1-b^{-k}} \\ 令ln(1-b^{-k}) + k * \frac{b^{-k} * lnb}{1-b^{-k}} =0\\ \Rightarrow ln(1-b^{-k}) * (1-b^{-k}) = -k * b^{-k} * lnb \\ \Rightarrow ln(1-b^{-k}) * (1-b^{-k}) = b^{-k} * lnb^{-k} \\ \Rightarrow 1-b^{-k} = b^{-k} \\ \Rightarrow b^{-k} = \frac{1}{2} \\ \Rightarrow e^{(-\frac{kn}{m})} = \frac{1}{2} \\ \Rightarrow \frac{kn}{m} = ln2 \\ \Rightarrow k = ln2 * \frac{m}{n} = 0.7 * \frac{m}{n} \\ \\ \\ 假设已知集合大小n，并设定好误判率p，需要计算给BF分配多大内存合适 \\ 当k已经取得最优时：P(error) = 2^{-k} \\ \Rightarrow log_2P = -k \Rightarrow k = log_2\frac{1}{P} \\ \Rightarrow ln2 * \frac{m}{n} = log_2\frac{1}{P} \\ \Rightarrow \frac{m}{n} = \frac{1}{ln2} *log_2\frac{1}{P} = -\frac{lnp}{{ln2}^2} \end{array}

有上述关系可知：

集合大小n、哈希函数的个数k和位数组大小m和误判率之间的关系:

\begin{array}{c} 误判率pfp= (1−e^\frac{-kn}{m})^k \end{array}

假设n和m已知，即已知位数组大小和集合元素个数，设定多少个哈希函数误判率能够达到最低呢？经过分析，最优的哈希函数个数为：

\begin{array}{c} k = \frac{m}{n} ln2 \end{array}

假设已知集合大小n，并设定好误判率p，需要计算给BF分配多大内存合适，即确定m的大小。

\begin{array}{c} m = -\frac{nlnp}{(ln2)^2} \end{array}

ClickHouse BloomFilter代码实现

上面的公式推导可以看到，当 $\frac{m}{n}$ 固定，存在一个 $k$ 使得误判率 $p$ 最低，这就是k的最右取值。如表就展示了不同m/n和 $k$ 的误判率

不同m/n和k的误判率

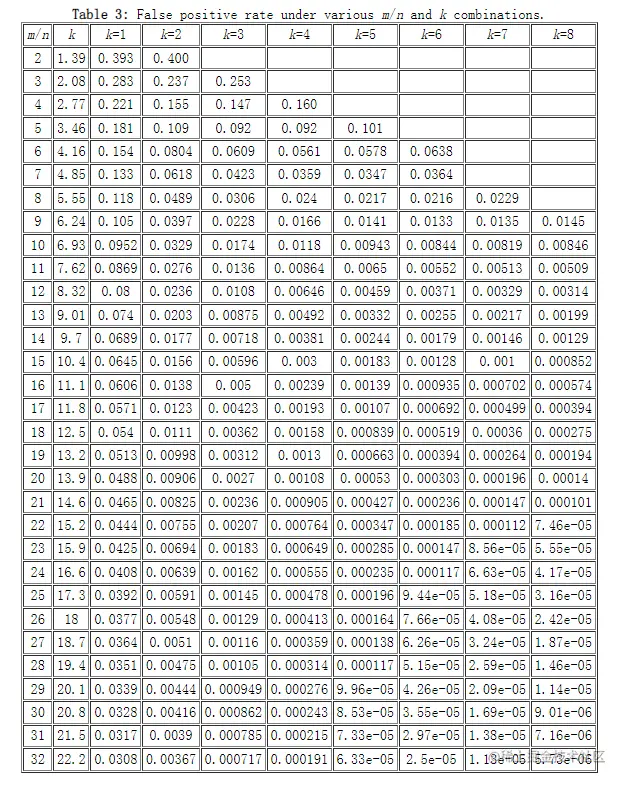
ClickHouse就利用了查表的原理，根据输入的误判率的大小，反推出k和 $\frac{m}{n}$ 的大小。相关实现详见src\Interpreters\BloomFilterHash.h中的calculationBestPractices函数。

    /**
     * @brief   理论上，在m/n固定的情况下，存在一个k值使得误判概率p最小。其中:
     *              m : 位数组的个数
     *              k : Hash函数的个数
     *              n : 集合的大小，放入BloomFiliter中元素的个数
     *          该函数实现可以根据用户传入的误判率的大小反推出该bf的最佳k和m/n取值,类似于loookupTable原理
     * 
     * @param max_conflict_probability      最大误判概率
     * @return std::pair<size_t, size_t>    由m/n和hash函数个数k组成的pair
     */
    static std::pair<size_t, size_t> calculationBestPractices(double max_conflict_probability)

ClickHouse的BloomFilter的实现源码位于src\Interpreters\BloomFilter.cpp,代码实现BloomFilterParameters封装了BF相关输入参数。

/**
 * @brief       BloomFiliter构造关键参数
 * 
 * @param filter_size_      位数组的个数m
 * @param filter_hashes_    Hash函数的个数
 * @param seed_             生成哈希函数的random seed
 * 
 */
BloomFilterParameters::BloomFilterParameters(size_t filter_size_, size_t filter_hashes_, size_t seed_)
    : filter_size(filter_size_), filter_hashes(filter_hashes_), seed(seed_)

BloomFilter负责实现布隆过滤器的功能，主要的功能接口:

// 布隆过滤器加入成员
void BloomFilter::add(const char * data, size_t len)

// 查找元素是否存在
bool BloomFilter::find(const char * data, size_t len)

布隆过滤器

基本原理

误判率计算

ClickHouse BloomFilter代码实现

参考资料