简介
在本教程中,我们将展示Python Sklearn(又称Scikit Learn)中PCA的实现。首先,我们将介绍降维的基本概念,以及它如何帮助你的机器学习项目。接下来,我们将简要地了解用于降维的PCA算法。最后,我们将用一个真实世界的数据集向你解释Sklearn中PCA的端到端实现。
1.机器学习中的维度诅咒
机器学习中的维度诅咒是指由于数据集的高维度而产生的问题。通俗地讲,维度可以指结构化数据集中的属性或字段的数量。在图像的情况下,维度可以被认为是像素的数量,以此类推。
通常在现实世界的机器学习问题中,数据集可能包含数百个维度,在某些情况下甚至是数千个。
- 人类无法将超过3维的数据可视化。因此,可视化和分析具有非常高维度的数据是非常具有挑战性的。
- 用机器学习算法来处理高维数据可能需要大量的计算资源。
- 用高维数据集生成的ML模型可能不会显示出良好的准确性或遭受过度拟合。
2.什么是降维?
降维是指将数据从高维空间转换到低维空间而不损失数据中的信息的各种技术。它本质上是一种避免我们上面讨论的维度诅咒的方法。
降维的优势
你可能想在数据集上应用降维,因为有以下好处
- 它减少了训练ML模型所需的计算时间。
- 它更容易在二维或三维图中对数据进行可视化分析。
- 它消除了数据中存在的冗余,只保留了相关信息。
降维技术
用于降维的各种方法包括:
- 主成分分析(PCA)
- 线性判别分析(LDA)
- 广义判别分析(GDA)
在这篇文章中,我们将只关注PCA算法和它在Sklearn中的实现。
3.什么是PCA?
主成分分析(PCA)是一种多变量统计技术,是由英国数学家和生物统计学家卡尔-皮尔逊提出的。
在这种方法中,我们将数据从高维空间转换到低维空间,并将信息损失降到最低,同时去除数据集中的冗余部分。
在应用PCA时,高维数据被映射成若干成分,这是应该提供的输入超参数。分量的数量必须小于数据的维度。这些分量以不同的表现形式持有实际数据的信息,如第一分量持有最大的信息,其次是第二分量,依此类推。
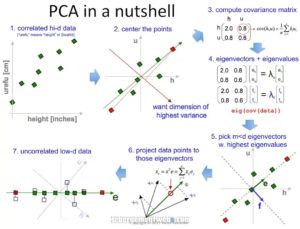
PCA涉及的步骤
在高层次上,PCA涉及的步骤有
- 在应用PCA之前,数据集的标准化是必须的,因为PCA对数值差异大的数据集相当敏感。
- 计算协方差矩阵
- 使用前一步的协方差矩阵计算特征值和特征向量,以确定主成分。
- 将特征值和其特征向量按降序排列。这里,数值最高的特征向量具有最高的意义,形成第一个主成分,以此类推。因此,如果我们选择取成分n=2,那么将选择前两个特征向量。
- 通过与上面选择的前n个特征向量相乘来转换数据的原始矩阵。
Scikit Learn对PCA的实现抽象了所有这些数学计算,并用PCA对数据进行转换,我们需要提供的只是我们希望得到的主成分数量。
4.我们的PCA实例概述
在这个使用Sklearn库的PCA例子中,我们将使用一个帕金森病的高维数据集,并向你展示--
- 如何使用PCA来可视化高维数据集。
- PCA如何避免分类器因高维数据集而过度拟合。
- PCA如何提高训练过程的速度。
那么让我们开始吧。
关于数据集
我们正在使用一个包含754个属性和756条记录的帕金森病数据集。正如你所看到的,它有754个属性,是高维度的。它包含一个属性 "class",包含0和1,表示没有或存在帕金森病。
该数据集可以从这里下载。
导入必要的库
我们首先加载本例所需的库。
在[0]:
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
读取CSV数据集
接下来,我们使用Pandas读取数据集CSV文件,并将其加载到一个数据框中。我们将通过使用head函数获取5条记录来快速检查数据集是否被正确加载。我们还通过使用数据框架的shape属性来验证行和列的数量。
最后,我们计算数据集中0和1两个类的数量。
In[1]:
df= pd.read_csv(r"pd_speech_features.csv")
df.head()
Out[1]:
| 性别 | PPE | DFA | RPDE | numPulses | numPeriodsPulses | 平均周期脉冲 | stdDevPeriodPulses | locPctJitter | locAbsJitter | ... | tqwt_kurtosisValue_dec_28 | tqwt_kurtosisValue_dec_29 | tqwt_kurtosisValue_dec_30 | tqwt_kurtosisValue_dec_31 | tqwt_kurtosisValue_dec_32 | tqwt_kurtosisValue_dec_33 | tqwt_kurtosisValue_dec_34 | tqwt_kurtosisValue_dec_35 | tqwt_kurtosisValue_dec_36 | 类 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0.85247 | 0.71826 | 0.57227 | 240 | 239 | 0.008064 | 0.000087 | 0.00218 | 0.000018 | ... | 1.5620 | 2.6445 | 3.8686 | 4.2105 | 5.1221 | 4.4625 | 2.6202 | 3.0004 | 18.9405 | 1 |
| 1 | 1 | 0.76686 | 0.69481 | 0.53966 | 234 | 233 | 0.008258 | 0.000073 | 0.00195 | 0.000016 | ... | 1.5589 | 3.6107 | 23.5155 | 14.1962 | 11.0261 | 9.5082 | 6.5245 | 6.3431 | 45.1780 | 1 |
| 2 | 1 | 0.85083 | 0.67604 | 0.58982 | 232 | 231 | 0.008340 | 0.000060 | 0.00176 | 0.000015 | ... | 1.5643 | 2.3308 | 9.4959 | 10.7458 | 11.0177 | 4.8066 | 2.9199 | 3.1495 | 4.7666 | 1 |
| 3 | 0 | 0.41121 | 0.79672 | 0.59257 | 178 | 177 | 0.010858 | 0.000183 | 0.00419 | 0.000046 | ... | 3.7805 | 3.5664 | 5.2558 | 14.0403 | 4.2235 | 4.6857 | 4.8460 | 6.2650 | 4.0603 | 1 |
| 4 | 0 | 0.32790 | 0.79782 | 0.53028 | 236 | 235 | 0.008162 | 0.002669 | 0.00535 | 0.000044 | ... | 6.1727 | 5.8416 | 6.0805 | 5.7621 | 7.7817 | 11.6891 | 8.2103 | 5.0559 | 6.1164 | 1 |
5行×754列
在[2]:
df.shape
出[2]:
(756, 754)
在[3]中:
df['class'].value_counts()
Out[3]:
1 564
0 192
Name: class, dtype: int64
5.用Sklearn的PCA实现高维数据集的可视化
正如我们前面所讨论的,人类不可能将超过3维的数据可视化。在这个数据集中,有754个维度。让我们用PCA来降低数据集的高维度,使其在2-D和3-D中都能可视化。
数据集的标准化
在应用PCA之前,必须对数据集进行标准化,否则会产生错误的结果。
这里我们使用sklearn.preprocessing模块中的StandardScaler()函数对训练和测试数据集进行标准化。
在[4]中:
X_Scale = scaler.transform(X)
- 同时阅读 - 为什么要在机器学习中进行特征缩放?
应用主成分=2的PCA
现在让我们对整个数据集应用PCA,并将其减少为两个成分。我们使用sklearn.decomposition模块的PCA功能。
在应用PCA之后,我们将结果与类别列串联起来,以便更好地理解。
In[5]:
pca2 = PCA(n_components=2)
principalComponents = pca2.fit_transform(X_Scale)
principalDf = pd.DataFrame(data = principalComponents, columns = ['principal component 1', 'principal component 2'])
finalDf = pd.concat([principalDf, df[['class']]], axis = 1)
finalDf.head()
Out[5]:
| 主成分1 | 主成分2 | 类 | |
|---|---|---|---|
| 0 | -10.184156 | 1.252252 | 1 |
| 1 | -10.621219 | 1.659891 | 1 |
| 2 | -13.507782 | -1.231873 | 1 |
| 3 | -9.277452 | 8.087223 | 1 |
| 4 | -7.142122 | 3.815401 | 1 |
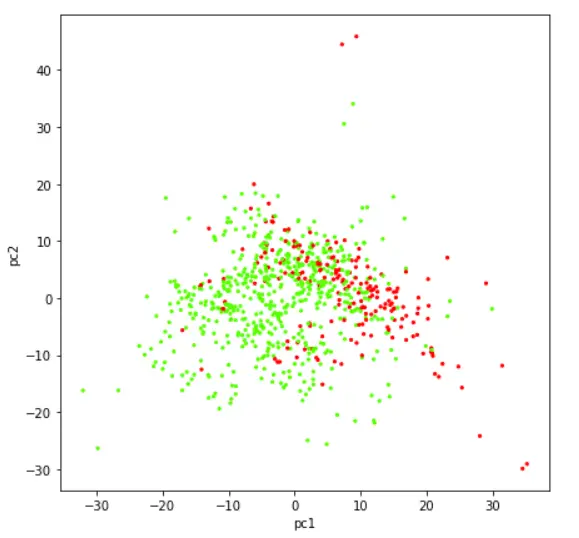
在二维散点图中实现数据的可视化
现在让我们借助于散点图来可视化已经被简化为两个组成部分的数据集。
In[6]:
plt.figure(figsize=(7,7))
plt.scatter(finalDf['principal component 1'],finalDf['principal component 2'],c=finalDf['class'],cmap='prism', s =5)
plt.xlabel('pc1')
plt.y;label('pc2')
输出[6]:
应用PCA,主成分=3
就像先前一样,让我们再次对整个数据集应用PCA,产生3个成分。
在[7]中:
pca3 = PCA(n_components=3)
principalComponents = pca3.fit_transform(X_Scale)
principalDf = pd.DataFrame(data = principalComponents, columns = ['principal component 1', 'principal component 2', 'principal component 3'])
finalDf = pd.concat([principalDf, df[['class']]], axis = 1)
finalDf.head()
Out[7]:
| 主成分1 | 主成分2 | 主成分3 | 种类 | |
|---|---|---|---|---|
| 0 | -10.184156 | 1.252253 | -7.185881 | 1 |
| 1 | -10.621219 | 1.659890 | -6.873706 | 1 |
| 2 | -13.507782 | -1.231873 | -7.076563 | 1 |
| 3 | -9.277453 | 8.087221 | 14.467958 | 1 |
| 4 | -7.142122 | 3.815398 | 15.474813 | 1 |
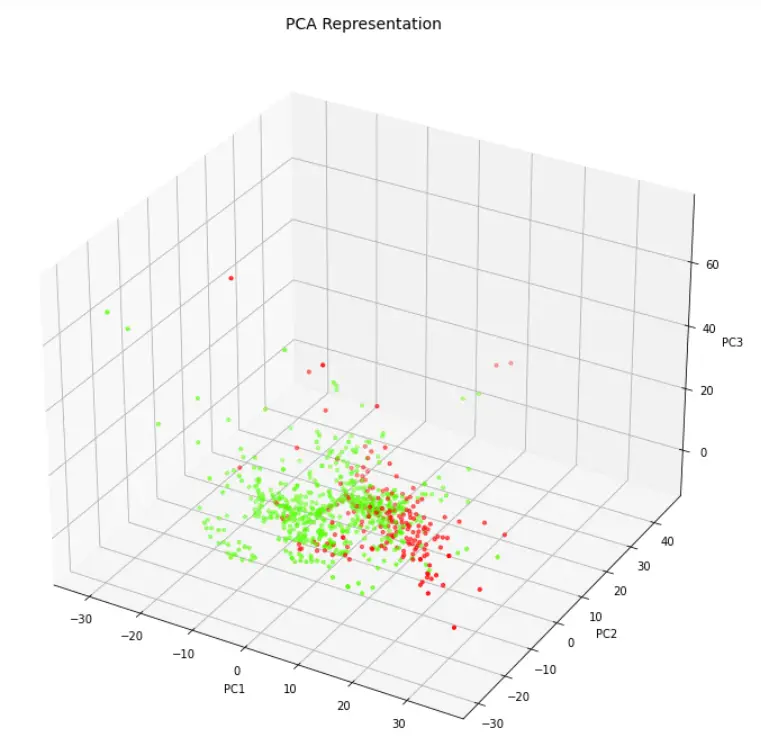
三维散点图中的数据可视化
让我们在三维散点图的帮助下,将PCA的三个组成部分可视化。
In[8]:
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(9,9))
axes = Axes3D(fig)
axes.set_title('PCA Representation', size=14)
axes.set_xlabel('PC1')
axes.set_ylabel('PC2')
axes.set_zlabel('PC3')
axes.scatter(finalDf['principal component 1'],finalDf['principal component 2'],finalDf['principal component 3'],c=finalDf['class'], cmap = 'prism', s=10)
输出[8]:
6.使用Sklearn的PCA提高速度并避免ML模型的过度拟合
现在我们将看到维度的诅咒在发挥作用。我们将创建两个逻辑回归模型--首先不应用PCA,然后通过应用PCA。我们将捕获它们的训练时间和准确度,并对它们进行比较。
将数据集分割成训练集和测试集
在这里,我们将把依赖标签列分离到y数据框中。所有剩下的列都放入X数据框。
然后,我们使用Sklearn的train_test_split函数将它们按70%-30%的比例分成训练集和测试集。
在[9]中:
X = df.drop('class',axis=1).values
y = df['class'].values
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.3,random_state=0)
数据集的标准化
这一次我们对训练和测试数据集分别进行标准化处理。
在[10]中:
scaler = StandardScaler()
# Fit on training set only.
scaler.fit(X_train)
# Apply transform to both the training set and the test set.
X_train_pca = scaler.transform(X_train)
X_test_pca = scaler.transform(X_test)
创建没有PCA的Logistic回归模型
在这里,我们创建了一个逻辑回归模型,可以看到该模型已经严重过拟合。训练精度是100%,测试精度是84.5%。
另外,请注意,这里的训练时间是151.7毫秒。
在[11]:
%%time
logisticRegr = LogisticRegression()
logisticRegr.fit(X_train,y_train)
y_train_hat =logisticRegr.predict(X_train)
train_accuracy = accuracy_score(y_train, y_train_hat)*100
print('"Accuracy for our Training dataset with PCA is: %.4f %%' % train_accuracy)
Out[11]:
"Accuracy for our Training dataset with PCA is: 100.0000 %
Wall time: 151.7 ms
在[12]中:
y_test_hat=logisticRegr.predict(X_test)
test_accuracy=accuracy_score(y_test,y_test_hat)*100
test_accuracy
print("Accuracy for our Testing dataset with tuning is : {:.3f}%".format(test_accuracy) )
Out[12]:
Accuracy for our Testing dataset with tuning is : 84.581%
用PCA创建Logistic回归模型
下面我们在对数据集应用PCA后创建了逻辑回归模型。可以看出,这次PCA数据集没有出现过拟合的情况。训练和测试的准确性都是79%,这是一个相当好的概括。
另外,在这里我们看到,训练时间只有7.96毫秒,比151.7毫秒明显下降。这里几乎快了20倍。你可能不太欣赏这种改进,因为两者都是以毫秒为单位的,但是当我们在处理大量的数据时,这种规模的训练速度改进就变得相当重要了。
在[13]:
%%time
logisticRegr = LogisticRegression()
logisticRegr.fit(X_train_pca,y_train)
y_train_hat =logisticRegr.predict(X_train_pca)
train_accuracy = accuracy_score(y_train, y_train_hat)*100
print('"Accuracy for our Training dataset with PCA is: %.4f %%' % train_accuracy)
Out[13]:
"Accuracy for our Training dataset with PCA is: 79.7732 %
Wall time: 7.96 ms
在[14]中:
y_test_hat=logisticRegr.predict(X_test_pca)
test_accuracy=accuracy_score(y_test,y_test_hat)*100
test_accuracy
print("Accuracy for our Testing dataset with PCA is : {:.3f}%".format(test_accuracy) )
Out[15]:
Accuracy for our Testing dataset with PCA is : 79.295%
结语
我们希望你喜欢我们的教程,现在能更好地理解如何在Python中使用Sklearn(Scikit Learn)实现PCA算法。在这里,我们用一个例子实际展示了PCA如何帮助实现高维数据集的可视化,减少计算时间,并避免过度拟合。