问题陈述

该问题要求设计一个数据结构来存储字符串和它们的计数。它应该能够在恒定时间内执行以下操作。

递增键数，inc(key)-- 插入一个计数为1的新键或增加一个现有键的计数。
Decrement key count, dec(key)-- 如果键的计数为1，我们就删除它，否则我们就递减它的计数。如果该键不存在，该函数不做任何事情。在此操作之前，保证键存在于数据结构中。
Get max key getMax(key)
-- 返回具有最大计数的键之一，否则如果没有键存在，则返回一个空字符串。
Get min key, getMin(key)
-- 返回具有最小计数的键之一，否则返回一个空字符串，表示没有键存在。

简单的方法（使用二维双链表）

我们的想法是使用一个有序的二维双链表，每一行对应一个计数值，同一行的所有键都有相同的计数值。为了便于理解，我把行和节点互换使用。

假设我们对这个数据结构进行以下操作：

将 "a "和 "b "增加4倍。
将 "c "和 "d "增加3倍
增加 "e "2次
增加 "f "和 "g "1次

下面是我们在上面的操作之后的额外操作的结果：

allOne.drawio-1-

当一个键被递增时，如果最后一行的计数=current_row.count+1，则将键从当前行移到最后一行，否则在当前行之前插入新行，其计数为current_row.count+1。
当一个键被递减时，如果最后一行的计数=current_row.count-1，则将键从当前行移到最后一行，否则在当前行之后插入行，其计数为current_row_count-1。

通过这种方法，获得最大值和最小值的时间是恒定的O(1)，我们只需在恒定的O(1)时间内返回第一行的第一个键为最大计数，最后一行的第一个键为最小计数，只要这些行是按降序排列。

这种方法的问题是，当我们增加键或减少键时，我们必须做更多的工作来维持这个降序，这使得时间复杂度为线性O(n)。

这可以通过采用一种以其高效的访问时间而闻名的数据结构来改善。一个哈希图。你可以在本帖末尾的链接中了解更多关于它是如何做到这一点的。
同时，我们将在下面讨论这种方法。

优化的方法（使用哈希图和双链表）

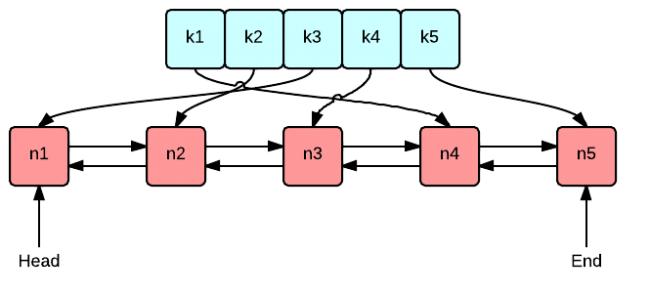
在这种方法中，我们的想法是使用一个双链表，这将导致O(1)操作的插入和删除，头部将有最大的计数，尾部的计数最少。因此，头部将在恒定的时间内返回最大键，尾部返回最小键。我们使用hashmap来引用列表节点以获得有效的访问时间，这也是我们在之前的天真方法中遇到的问题。

递增

条件1：键存在于列表中

检查key是否在第一行。
如果上述条件成立，在当前行之前创建并插入一个新行，其计数值为currentRow.count + 1，其数据为key(string)。
否则从当前行中删除key(string)，并将其放在当前行之前的行中，其计数为currentRow.count+1。

条件2：键不存在于列表中

检查列表是否为空。
如果上述条件成立，创建并插入一个新的节点，其计数为1，并将key(string)作为其数据放在列表的最后。
否则，存在一个节点，所以将key(string)放在列表最后的现有节点中。

递减

条件1：键存在于列表中

检查带有key的节点的值是否为1，如果是，将其从列表中删除。
检查key是否在第一个节点上。
如果上述条件成立，在当前行之后创建并插入一个新行，其计数值为currentRow.count - 1，其值为key(string)。
否则从当前节点移除key(string)并将其放在列表的最后一行。

条件2：键不存在于列表中
键不存在于列表中，所以不做任何事情：

getMax()

检查列表是否为空，不返回。
否则返回第一个节点的第一个键。

getMin()

检查列表是否为空，并不返回。
否则返回最后一个节点的第一个键。

代码

class AllOne{
    public:
        //create the structure of a row
        struct row{
            list<string> strings;
            int val;
            row(const string &s, int x) : strings({s}), val(x){}
        };
        
        //initialize hashmap and doubly linked list
        unordered_map<string, pair<list<row>::iterator, list<string>::iterator>> strMap;
        list<row> strList;
        
        //increment procedure
        void inc(string key){
            //the key does not exist in the map
            if(strMap.find(key) == strMap.end()){
                if(strList.empty() || strList.back().val != 1){
                    auto newRow = strList.emplace(strList.end(), key, 1);
                    strMap[key] = make_pair(newRow, newRow->strings.begin());
                }else{
                    auto newRow = --strList.end();
                    newRow->strings.push_front(key);
                    strMap[key] = make_pair(newRow, newRow->strings.begin());
                }
            }else{
                //key exist in the map
                auto row = strMap[key].first;
                auto col = strMap[key].second;
                auto lastRow = row;
                --lastRow;
                if(lastRow == strList.end() || lastRow->val != row->val + 1){
                    auto newRow = strList.emplace(row, key, row->val + 1);
                    strMap[key] = make_pair(newRow, newRow->strings.begin());
                }else{
                    auto newRow = lastRow;
                    newRow->strings.push_front(key);
                    strMap[key] = make_pair(newRow, newRow->strings.begin());
                }
                row->strings.erase(col);
                if(row->strings.empty())
                    strList.erase(row);
            }
        }

        void dec(string key){
            //key does not exist in the map
            if(strMap.find(key) == strMap.end())
                return;
            else{
                //key exists in the map
                auto row = strMap[key].first;
                auto col = strMap[key].second;
                if(row->val == 1){
                    row->strings.erase(col);
                    if(row->strings.empty())
                        strList.erase(row);
                    strMap.erase(key);
                    return;
                }
                auto nextRow = row;
                ++nextRow;
                if(nextRow == strList.end() || nextRow->val != row->val - 1){
                    auto newRow = strList.emplace(nextRow, key, row->val - 1);
                    strMap[key] = make_pair(newRow, newRow->strings.begin());
                }else{
                    auto newRow = nextRow;
                    newRow->strings.push_front(key);
                    strMap[key] = make_pair(newRow, newRow->strings.begin());
                }
                row->strings.erase(col);
                if(row->strings.empty())
                    strList.erase(row);
            }
        }
        //get first key in first row in the map
        string getMax(){
            if(strList.empty())
                return "";
            return strList.front().strings.front();
        }
        
        //get the first key in the last row in the map
        string getMin(){
            if(strList.empty())
                return "";
            return strList.back().strings.front();
        }
};

时间和空间复杂度分析

通过使用哈希姆，我们跟踪一个键的位置，访问时间是O(1)，使用一个链接列表来存储节点，增量和减量也是O(1)。总的来说，这些操作的运行时间是恒定的O(1)

另一方面，空间复杂度将是线性的O(n)，n是我们需要存储的键的数量。

问题

你能想到这种数据结构在现实世界中的应用吗？

O'one数据结构的详细指南