本文已参与「新人创作礼」活动,一起开启掘金创作之路。
一、什么是树?
[总结] 不同于我们之前所学的链表和数组,树是一种非线性的结构。判断是否为树只需注意一点:
- 每个结点有且只有一个父节点(否则就变成了图)
二、树的重要术语
这是一棵树:
①结点之间的关系
②度的概念
③层次的概念
④叶节点/分支结点
⑤祖先与子孙
三、树与二叉树
①树来存储数据? 【答】树存储数据的效率比较低下,原因之一在于无法知道每一层结点的个数。因此若要使用树来存储数据,最恰当(没有之一)的结构是孩子兄弟表示法:

②二叉树 二叉树的存储效率非常之高,因为每一个父节点只有确定的两个子节点
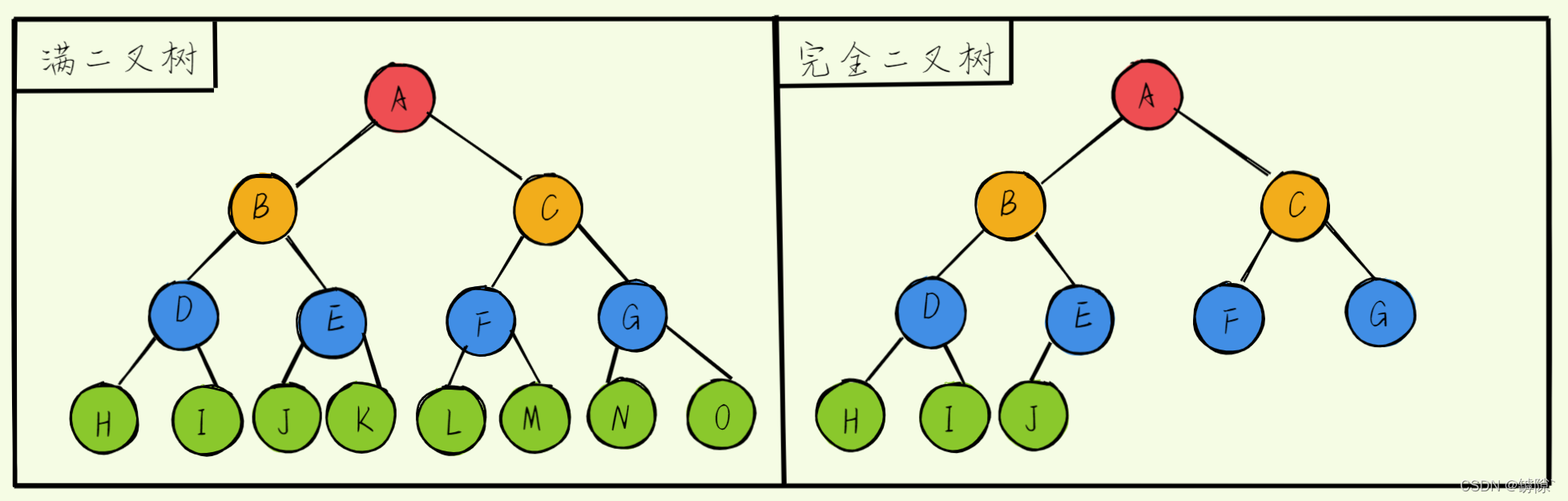
③两种特殊的二叉树
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树(特殊的完全二叉树)。
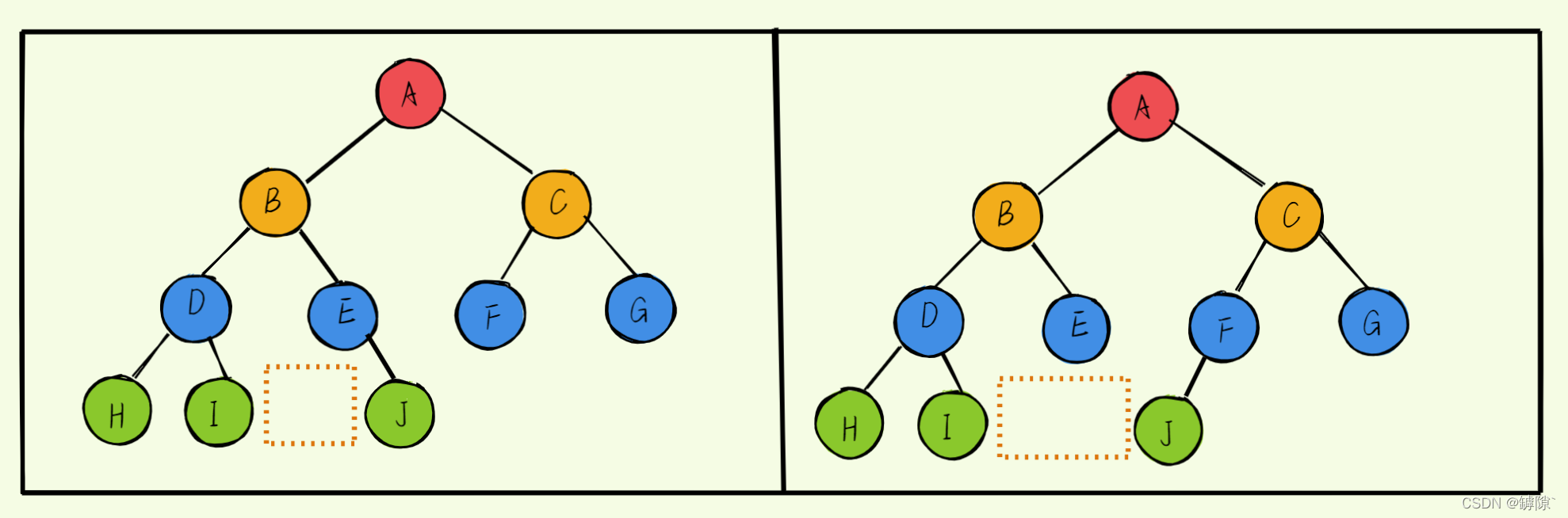
- 完全二叉树:对于深度为K的树,K-1层都是满的。最后一层如果不满但各个结点之间还是连续的(以下两张图都不是完全二叉树,因为他们不连续,中间有空隙)。
四、二叉树的重要性质
①重要性质:
- 对任何一棵二叉树, 如果度为0其叶结点个数为 N0, 度为2的分支结点个数为 N2,则有 N0 = N2 + 1 (数学归纳法证明,对任何树都满足)
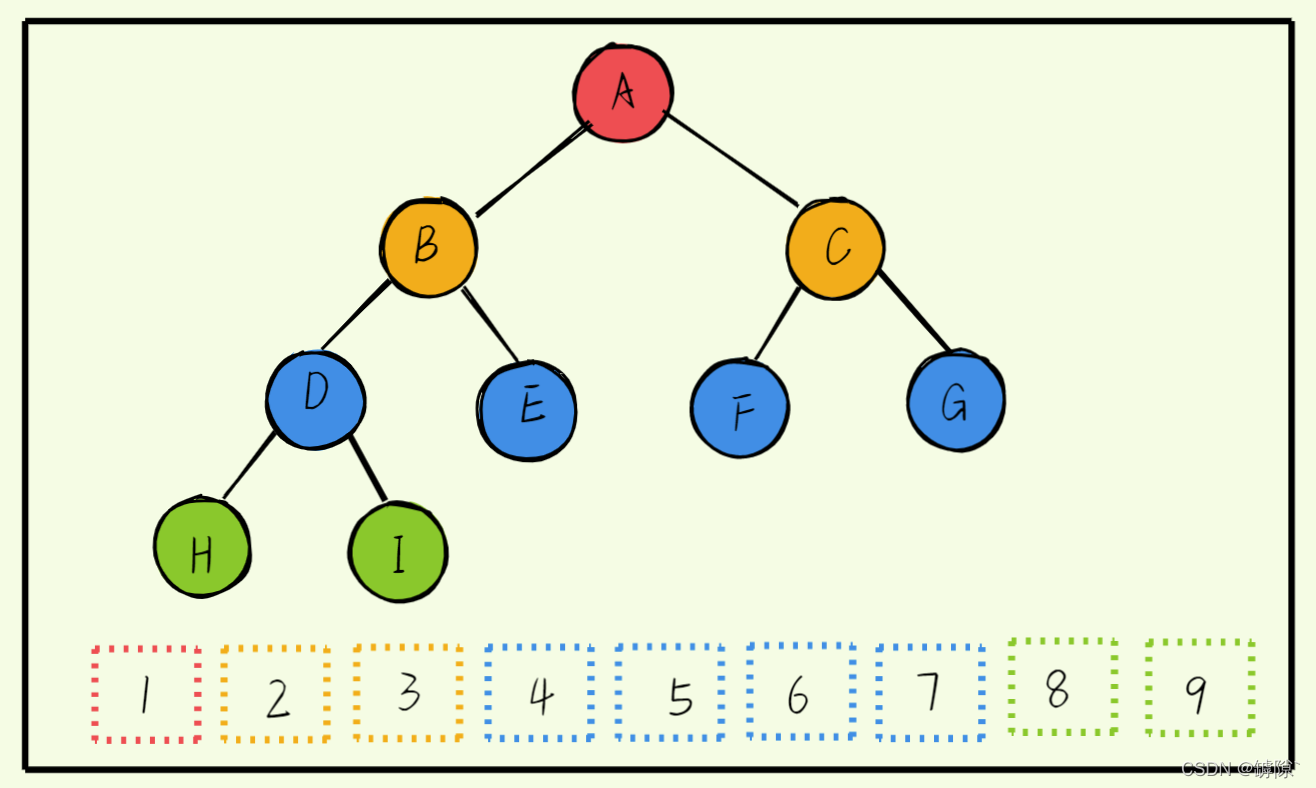
- 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h = log2(n + 1)
- 将二叉树映射到数组中,则父节点与左右孩子结点的关系是: leftson = parent * 2 + 1 rightson = parent * 2 + 2
②练习题1.
【提示】 总结点数为N,则一共有N-1条边,列方程解的答案为C 练习题②.
【提示】 最极端的情况,每一个结点的度都是4。答案选B 练习题③
【提示】 完全二叉树,则度为1的结点要么为0个要么为1个。在结合N0 = N2 + 1求解。答案为C