寻找最小切口的Karger算法

在这篇文章中，我们将探讨Karger算法是如何在图中寻找最小切口的，以及它的C++实现。这是一种基于图的随机算法。

目录：

1. 什么是最小切口？
2. 卡格尔的算法
3. 成功概率和时间复杂度
4. Karger算法的代码实现

前提是：随机化算法，最小切口

让我们开始学习Karger的算法来寻找最小切口。

什么是最小切口？

图中的最小切割指的是图中必须断开的边的数量，以便将图分成两个不相交的部分。让我们举几个象形的例子来了解更清楚的概念。

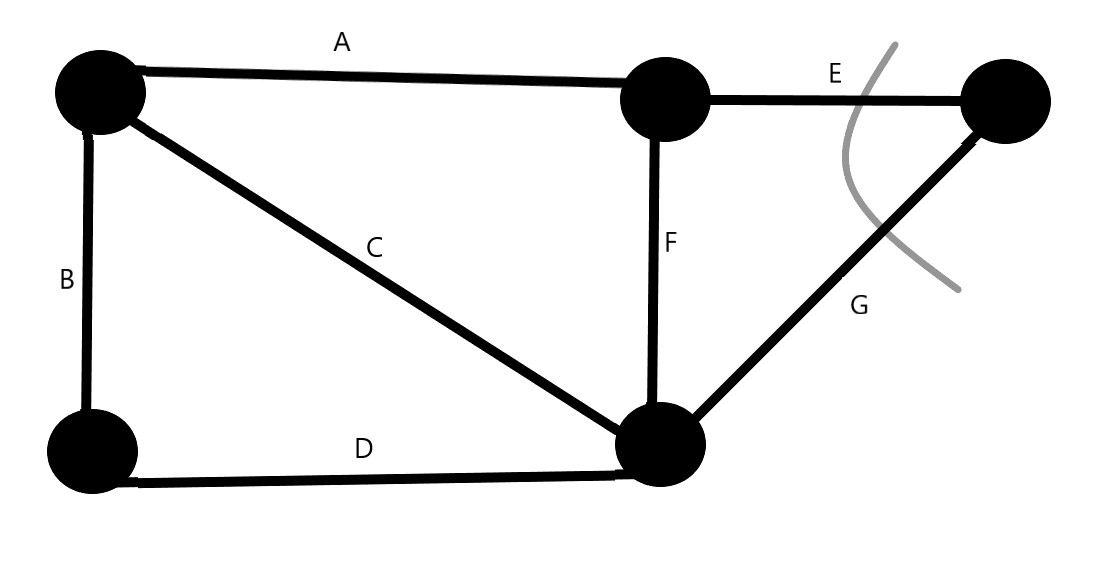
在这个例子中，最小切割将是切断边E和G，因此，最小切割=2。

最小切口也可以通过切断边B和边D来实现：

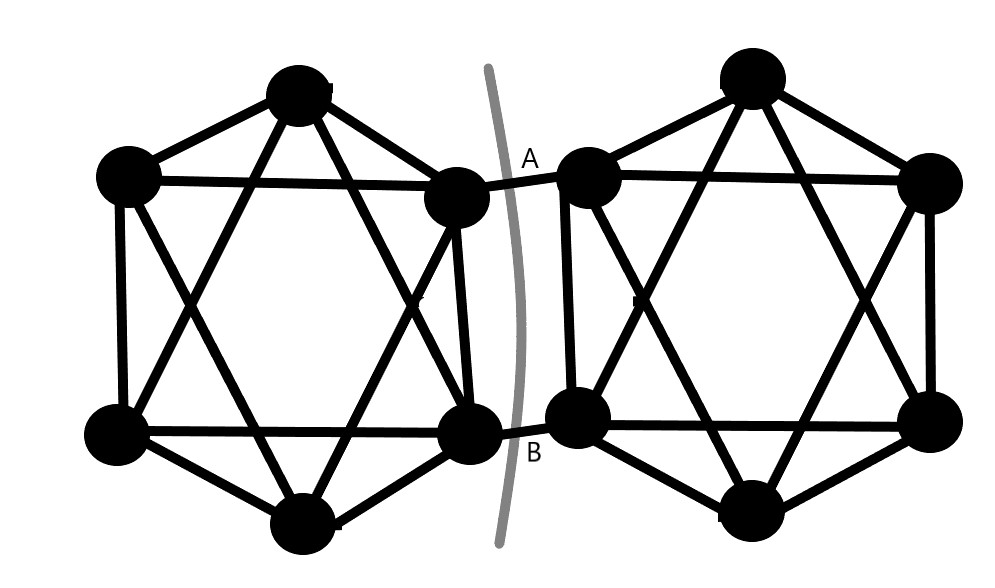
在这个例子中，我们看到最小切口是通过切断边A和B来实现的，这就把图形分成了两个对称的部分。因此，最小切割=2。
我们看到，两个不相交部分的大小对我们来说并不重要，也就是说，这两个部分的大小可以大不相同，也可以几乎相等。

Karger算法

Karger算法是一种随机算法，用于寻找无权无向图中的最小切口，在这种算法中，我们随机抽取一条边，并将边的两端收缩或凝聚成一个点。因此，所有的点最终都会结合成超级节点，而图的大小则不断减少。同时，所有的自循环都被删除。在算法的最后，我们留下了两个由若干条边连接的节点。连接两个最终超级节点的边的数量给出了所需的最小切割。

因此，我们有以下算法：

While there are more than 2 vertices-
      a) Pick a random edge (x, y) in the contracted graph.
      b) Merge the points x and y into a single vertex (update the contracted graph).
      c) Remove self-loops.

Return cut represented by two vertices.

让我们回到第一个例子，直观地看看这个算法的作用。

• 所以，在第一步中，我们合并了边B两端的顶点。因此，我们最终得到一个超级节点，它现在成为边A、C和D的一端。所以，我们省略它。

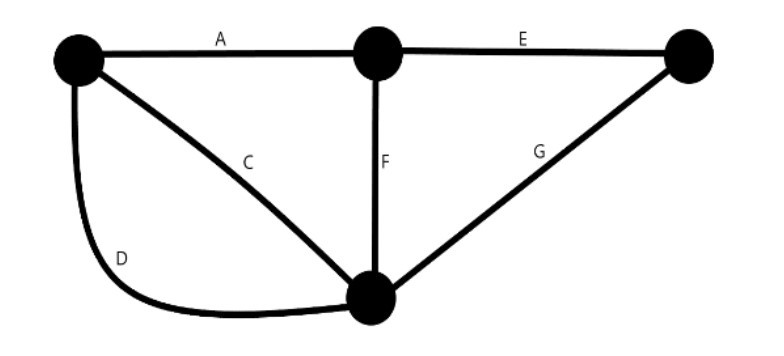
• 我们收缩边C（或D，意义相同）。边缘C和D都将形成自循环，因此被省略。我们现在有一个超级节点，它成为边A和边F的另一个端点。

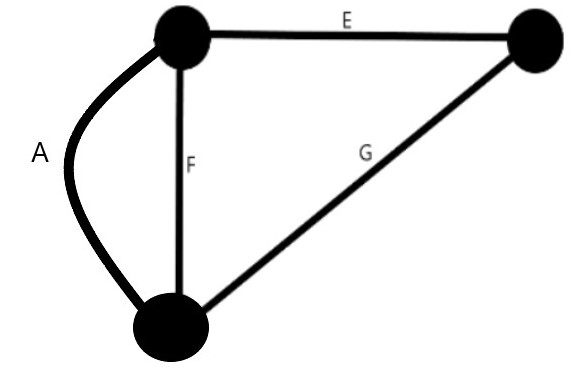
• 我们选取边A（或F），将两端的点汇合。因此，A和F都形成了自循环，并从图中被删除。我们最终得到一个由边E和G连接的两个顶点的图形。

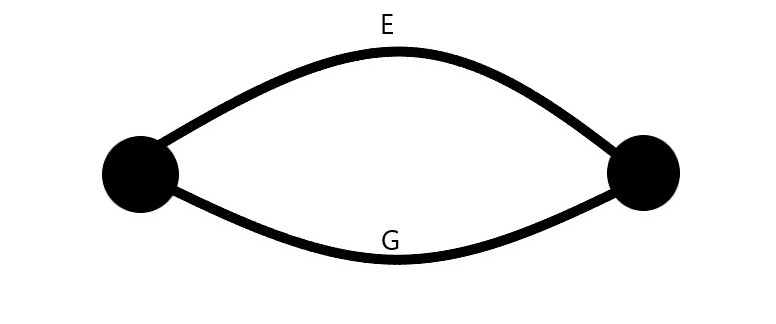
由于只剩下两个顶点，算法终止，2（图中剩余的边数）被作为最小值返回。

成功概率和时间复杂度

由于Karger的算法是一种随机算法，它在第一次运行时并不总是能得出正确的答案。事实上，达到最小切割的概率是2/n(n-1)，这很低。因此，为了确保最小切口，我们必须运行足够多的算法次数。 据观察，我们至少需要运行*n2 log(n)*次才能到达最优解，其中n是图中顶点的数量。

任何一对顶点的合并以及去除自循环的时间复杂度是O(n)。由于这两项工作都将在图上进行，直到只剩下2个顶点，所以单次运行的时间复杂度为O(n2)。但为了达到最佳效果，我们将运行该算法n2 log(n)次，因此我们的整体复杂度飙升至O(n4 log(n))。

Karger算法的代码实现

在c++的实现中，我们将使用邻接矩阵来存储图形。这将被定义为一个向量的向量vector<vector<int>> edges 。矩阵中的行和列的数量等于图中顶点的数量vertices 。我们将制作一些set和get函数来设置图中的值，并将其检索出来。我们也有关于矩阵大小的get和set函数。
除此之外，我们还有对算法至关重要的三个主要函数--remove_self_loops() 、merge_vertices() 和kargers_algorithm() 。让我们逐一看看这些函数。

• remove_self_loops() 迭代图形并删除所有自循环，即开始和结束于同一顶点的边。由于我们使用的是邻接矩阵，这个函数将把所有对角线元素设置为0。

graph& remove_self_loops(){
        for(int i=0;i<vertices;i++){
            set(i,i,0);
        }
        return *this;
   }

我们将在以后检查整个程序时看到set() 函数的定义。

• merge_vertices() 函数需要两个参数u和v，它们是要合并的顶点。该函数遍历图形，对于每一个顶点i，它将其所有的边（i,u）添加到顶点v，然后，将顶点u的边设置为0。由于图形是无定向的，这也是对所有（u,i）对进行的。

graph& merge_vertices(int u, int v){
   if(u< vertices && v< vertices){
        for(int i=0;i<vertices;i++){
            set(i,v,get(i,u)+get(i,v));
            set(i,u,0);
            set(v,i,get(u,i)+get(v,i));
            set(u,i,0);
          }
   }
   return *this;
   }

• 现在，我们来看看我们的kargers_algorithm() 函数。这个函数在图中有两个以上的顶点时进行迭代，它随机挑选两个顶点，将它们合并并删除自循环。因此，我们有了代码：

void kargers_algorithm(graph& g)
{
   g.remove_self_loops();
   while (g.count_vertices() > 2)
   {
      int u = 0, v = 0;
      do
      {
         u = rand() % g.get_size();
         v = rand() % g.get_size();
      }
      while (g.get(u, v) == 0);
   // Merge both vertices
      g.merge_vertices(u, v);
   //Remove self-loops
      g.remove_self_loops();
   }
   return;
}

该函数只定义了算法的一次运行。因此，为了优化，我们将在我们的main() 函数中多次调用它。
现在，我们可以看到最终的代码，其中有一个图类和它的所有成员函数，看看它是如何形成的：

#include <bits/stdc++.h>
using namespace std;

class graph{
public:
    int vertices;
    vector<vector<int>> edges;

   void set(int r, int c, int d) {
       edges[r][c] = d;
       return;
       }
   int get(int r, int c) {
       return edges[r][c];
       }

   void set_size(int s) {
       vertices = s;
       edges.resize(vertices * vertices);
       return;
       }
   int get_size(){
       return vertices;
       }
   int count_vertices() {
        int v=0;
        for(int i=0;i<vertices;i++){
             for(int j=0;j<vertices;j++){
                if(get(i,j)>0){  
                v++; break;
                }
            }
        }
        return v;
   }
   int count_edges(){
        int e=0;
        for(int i=0;i<vertices;i++){
            for(int j=0;j<vertices;j++){
                e+=get(i,j);
            }
        }
        return e/2;
   }

   graph& remove_self_loops(){
        for(int i=0;i<vertices;i++){
        set(i,i,0);
        }
        return *this;
   }

   graph& merge_vertices(int u, int v){
   if(u< vertices && v<vertices){
        for(int i=0;i<vertices;i++){
            set(i,v,get(i,u)+get(i,v));
            set(i,u,0);
            set(v,i,get(u,i)+get(v,i));
            set(u,i,0);
          }
   }
   return *this;
   }
};
void kargers_algorithm(graph& g)
{
   g.remove_self_loops();
   while (g.count_vertices() > 2)
   {
      int u = 0, v = 0;
      do
      {
         u = rand() % g.get_size();
         v = rand() % g.get_size();
      }
      while (g.get(u, v) == 0);
   // Merge both vertices
      g.merge_vertices(u, v);
   //Remove self-loops
      g.remove_self_loops();
   }
   return;
}
int main()
{
     graph g;
     g.vertices=6;
     g.edges={{0 ,1 ,0, 1, 1, 0},
              {1, 0, 1, 0, 1, 0},
              {0, 1, 0, 0, 1, 1},
              {1, 0, 0, 0, 1, 0},
              {1, 1, 1, 1, 0, 1},
              {0, 0, 1, 0, 1, 0}};
      graph ming; ming.set_size(0);

      cout << "Input vertex count: " << g.count_vertices() << endl;
      cout << "Input edge count: " << (g.count_edges()) << endl;

      int n = g.count_vertices();
      float ln = log((float) n);
      float runs = n * n * ln, mincut = INT_MAX;

      for (int i = 0; i < runs; ++i)
      {
         graph copy = g;
         kargers_algorithm(copy);
         int cut = copy.count_edges();
         if (cut < mincut)
         {
            mincut = cut;
            ming = copy;
         }
      }
      cout << "Output vertex count: " << ming.count_vertices() << endl;
      cout << "Output edge count: " << ming.count_edges()<< endl;
    cout<< "Minimum cut for the graph is "<< mincut<<endl;
    return 0;
}

在主函数中，我们已经使用适当的数据类型计算了运行次数=n2log(n)。我们初始化了一个新的图形明，以存储具有最小切割的图形。我们还创建了一个图形副本，它被初始化为我们给定的图形g，这个副本被算法修改以得到最小切割。如果达到的切割量低于当前的最小切割量mincut，那么mincut值就会被更新，图明就会存储最小切割量的图。
输出:

Input vertex count: 6
Input edge count: 9
Output vertex count: 2
Output edge count: 2
Minimum cut for the graph is 2

因此，在OpenGenus的这篇文章中，我们已经探讨了什么是图形的最小切割，Karger的算法是为了找出相同的算法以及它的C++实现。继续学习!