最佳优先搜索是一种搜索算法,在一组定义的规则上工作。它利用了优先队列和启发式搜索的概念。该算法的目标是以最短的路线从初始状态到达目标状态或最终状态。
目录:
- 什么是搜索算法?
- 什么是最佳第一搜索?
- 最佳第一搜索算法的比较
- 最佳优先搜索的例子
- 最佳第一搜索算法的优点和缺点
我们将开始讨论最佳第一搜索算法。
什么是搜索算法?
1997年,"深蓝 "人工智能在国际象棋中击败了传奇人物加里-卡斯帕罗夫,2016年,"阿尔法围棋 "击败了围棋冠军。随着时间的推移,人工智能模仿人类并超越其心理能力的能力已经超过了人类。
搜索算法构成了此类程序的基础,它们被用于课程和成本优化、行动规划、信息挖掘、机械技术、独立驾驶、计算科学、编程和设备检查、假设论证等领域。
就像它一样,相当多的人工智能问题可以被认为是这样的,其目标是通过状态变化规则从初始点达到最终目标。因此,搜索空间或选项被描述为一个图(或一棵树),重点是通过最短的路径从基础状态到达目标。
搜索算法可以分为两种类型
- 无信息的方法:在这种方法中没有提供额外的信息。这种方法的例子是搜索的广度或搜索算法的深度。
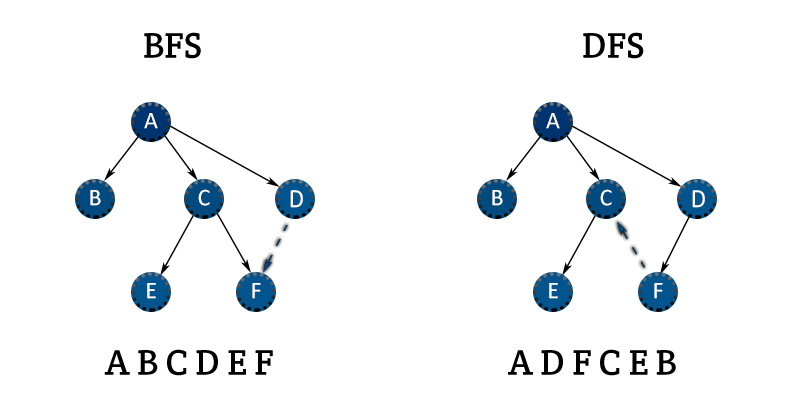
- 有信息的方法:也被称为启发式方法,通过使用额外的信息来寻找下一步要采取的行动。
如何执行这一算法,解释如下
什么是最佳优先搜索?
与不知情的搜索不同,在最佳优先搜索中,代理人盲目地穿越到下一个节点,使用一个评估函数来确定哪个邻居节点最适合移动。
它使用优先队列和启发式搜索的概念。
最佳第一搜索算法的方法
- 创建两个空列表
- 从最初的节点开始,将其添加到有序的开放列表中
- 接下来重复下面的步骤,直到到达最后的节点或端点
- 如果开放列表是空的,则退出循环,并返回一个False语句,表示无法到达最终节点。
- 选择开放列表中的顶级节点,并将其移到封闭列表中,同时保持对父节点的跟踪
- 如果被移除的节点是终点节点,则返回True语句,这意味着已经找到了一条路径,并将该节点移到封闭列表中。
- 然而,如果它不是端点节点,则列出它的所有相邻节点,并将它们添加到开放列表中。
- 根据评估函数对节点重新排序。
这个算法将首先遍历队列中最短的路径。该算法的时间复杂度为O(n*log(n)) 。
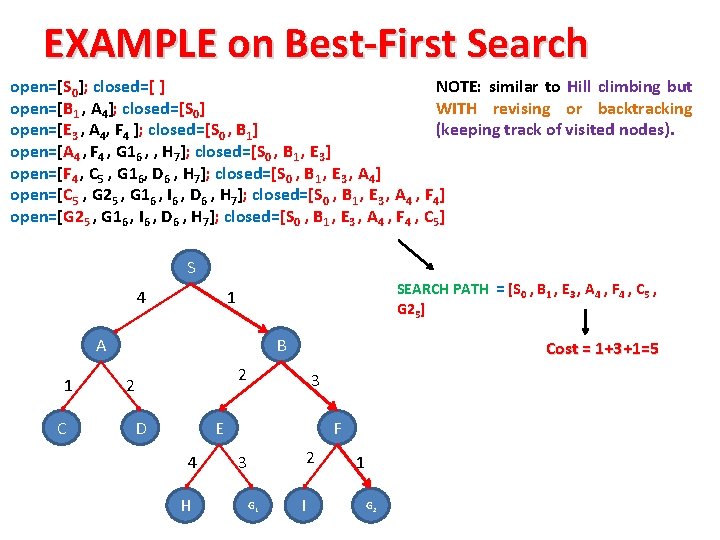
最佳优先搜索算法的比较
A*算法
在最佳优先搜索算法中,系统根据启发式函数移动到下一个状态,选择最低的启发式值,然而在A*算法中,下一个状态取决于启发式以及g组件,即从初始状态到特定状态的路径。
最佳第一算法并不考虑通往特定状态的路径的成本。它所关心的是,从当前状态到下一个状态的启发式算法是最低的。A*算法在考虑启发式算法的同时,也考虑了去往该状态的成本。
A*也允许回到之前的状态,但是在最佳搜索中,决定是最终的。
贪婪
贪婪地逐个建立解决方案,总是选择能提供最大利益的下一个节点,而最佳优先搜索算法则根据启发式函数选择下一个节点。
贪婪地选择下一个节点的短期最佳方案,移动到下一个节点的成本越低,它将采取特定的路线,最佳优先搜索算法根据所有选项中最便宜的路径来选择下一个最佳方案。
最佳优先搜索的例子
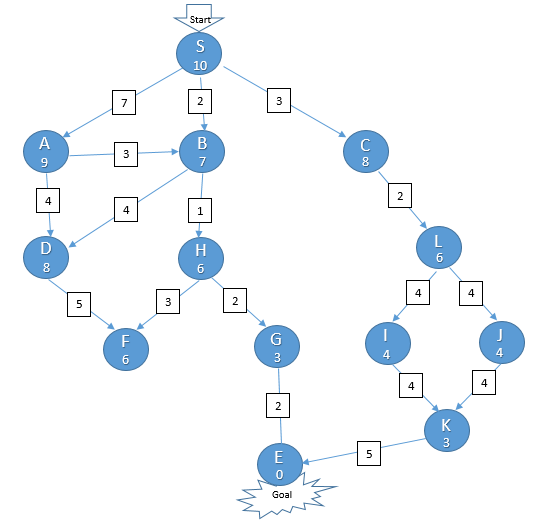
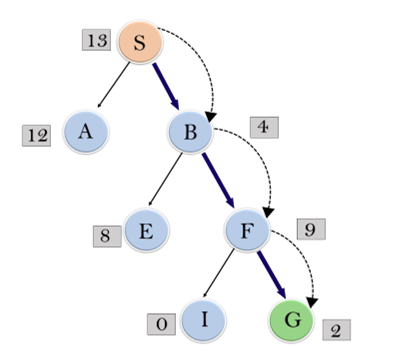
这里我们有一个图,我们的目标是从节点S到节点G的穿越。
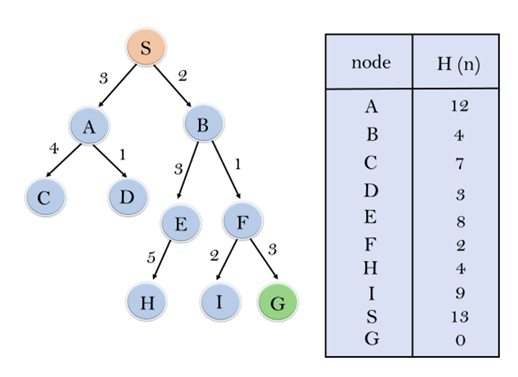
与每个节点相关的启发式价值已经提供。
我们使用两个列表open和close,最初只有节点S存在于open列表中,close是空的:
open : [S]
Closed:[]
在第一次迭代中,我们弹出节点S并将其移到封闭列表中,邻居节点被添加到开放列表中
开放:[A,B]
关闭:
[S]
[S]
在第二次迭代中,比较节点A和B的启发式数值,因为B的启发式数值较低,所以它被弹出并移到关闭列表中:
打开:[E,F,A]
关闭:[S,B]。
在第三次迭代中,比较E,F和A的启发式数值,由于F的启发式最低,它被添加到关闭列表中:
打开:[I,G,E,A]
关闭:[S,B,F]。
在第四次迭代中,我们的目标节点在开放列表中,因此我们选择该节点并将其移到封闭列表中:
开放:[I,E,A]
关闭:[S,B,F,G]
采取的路径是S->B->F->G
最佳优先搜索算法的优势和劣势
优点
- 与DFS等算法相比,效率更高
- 具有DFS和BFS的优点,因为可以在二者之间进行切换
劣势
- 算法可能会陷入循环之中
通过OpenGenus的这篇文章,你一定对最佳优先搜索算法有了完整的了解。