如何编写一个Java程序来获取斐波那契数列（多种方法）

斐波那契数列是一种特殊的数列，以0 和1 开始，这两个数字之后的每一个数字都是前面两个数字之和。

斐波那契数列是这样的：0, 1, 1, 2, 3, 5, 8, 13, 21, … ，依次类推。它最早是在印度数学中描述的：

源于此。缩放器专题

斐波那契数列被用于金融和科技等许多领域。你也可以在许多自然过程中看到它。

Guy Murchie的名言很好地解释了斐波那契数列在自然界中的重要性

"斐波那契数列原来是理解自然界如何设计的关键......并且是......同样无处不在的球体音乐的一部分，它将和谐构建在原子、分子、晶体、贝壳、太阳和星系中，使宇宙歌唱。"-盖伊-默奇，《生命的七个奥秘》，科学与哲学的探索

你知道这些事实吗？

• 斐波那契数列中任何两个连续数字的比率大约为1.6。例如：21 / 13 = 1.61和55 / 34 = 1.61
• 11月23日是斐波那契日，因为这一天的日期与斐波那契数列的mm/dd格式相似，因为它是（11/23）。

如何使用自上而下的方法计算斐波那契数列

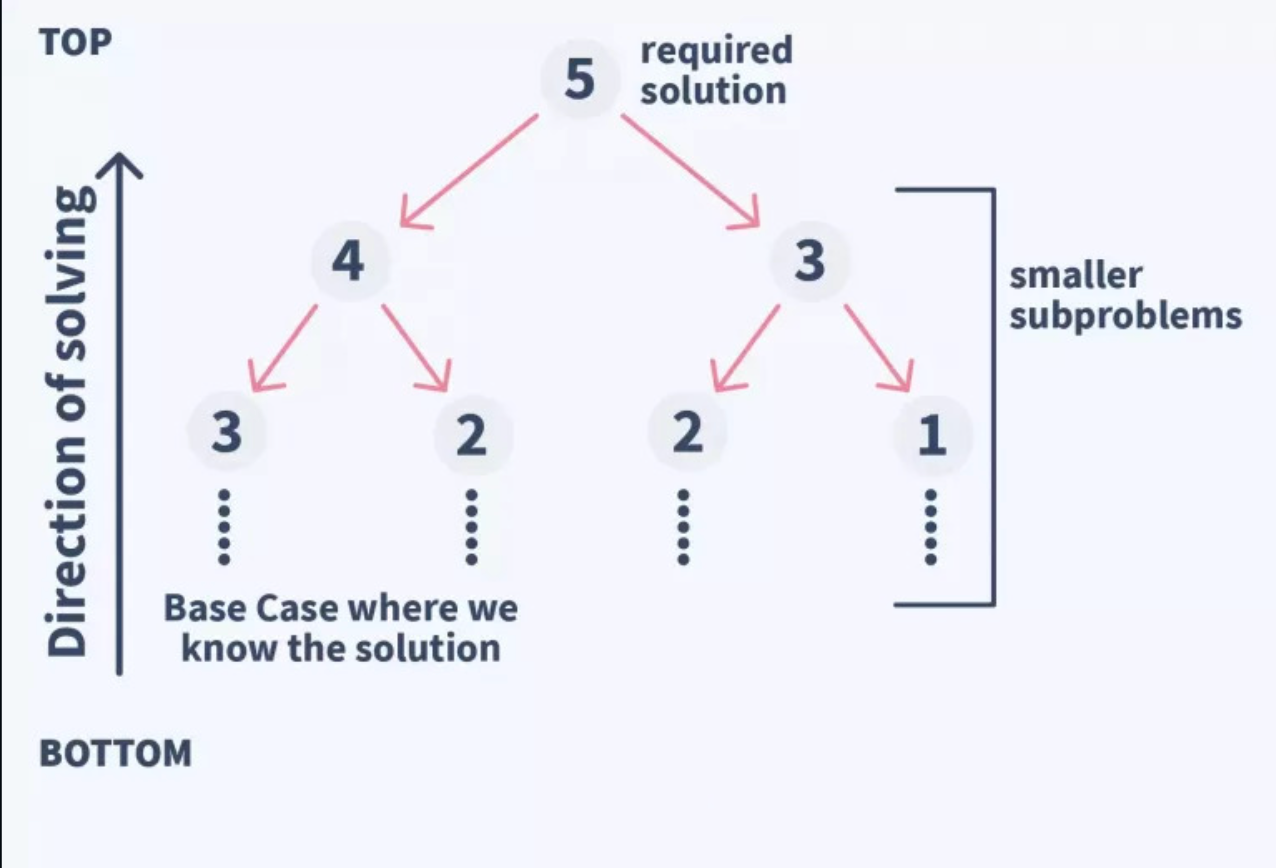
在这种自上而下的方法中，我们将所需指数的值计算为前两个指数的值之和。

如果我们无法获得前两个数值，我们也要对它们重复同样的过程。

如果它们的值也不可用，我们就重复同样的过程，直到我们得不到这两个值。这是一种理论驱动的方法。

我们在这里使用树状的方法--我们只是寻找前两个值，如果这些值不可用，我们就重复这个过程，直到我们没有得到这两个值。

我们将复杂的算法分解成更小的片段，这些片段可以被称为模块。而我们可以将这些模块进一步分解成更小的片段，直到它们不能再被分解：

源于此。缩放器专题

自上而下方法的算法

首先，你把输入的'n'拿到斐波那契数列中的相应数字。

然后，你计算所需指数的值，作为前两个指数的值的总和（也就是把n-1 指数和n-2 指数的值相加）。如果没有找到前两个指数的值，你将以同样的方式来寻找该指数的值。

每当你得到前两个连续索引的值时，你就将它们相加，并将结果作为下一个索引的值返回。

然后，你将“n - 1” 索引和”n - 2 ” 索引的值相加，并返回所需的值。

自上而下方法的优点

• 调试你的项目变得更有效率。
• 实现代码变得更容易。
• 它使代码易于解决和管理。
• 由于有独立的模块，测试过程变得更容易。

自上而下方法的缺点

• 对其他模块有很高的依赖性。一个模块的变化会影响到所有其他模块。
• 与动态编程中的 "自下而上 "方法相比，由于递归的原因，这种方法速度较慢。

如何使用自下而上的方法来计算斐波那契数列

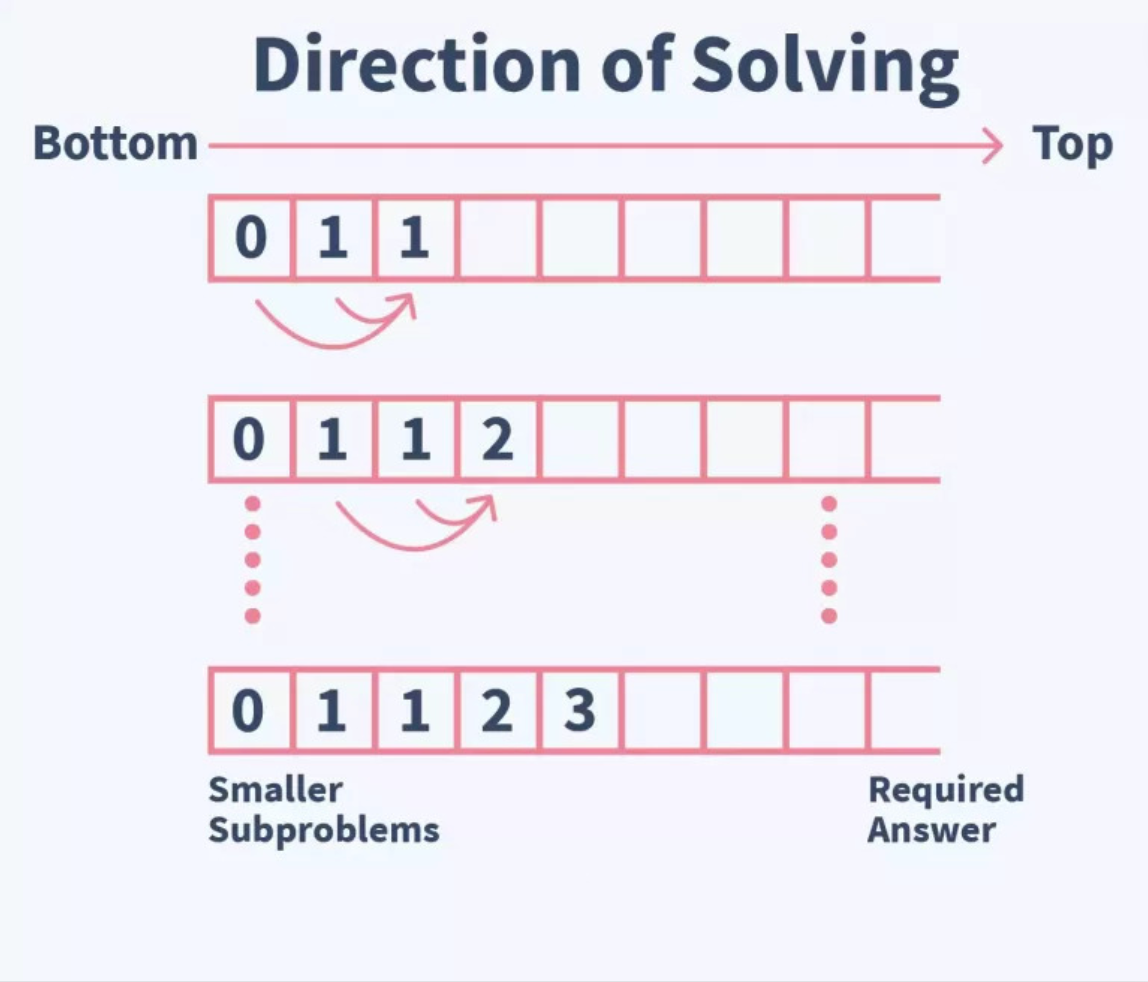
在这种自下而上的方法中，我们创建一个数组，并将前两个索引的值分别填为0 和1 。

之后，我们用这两个值来计算所有索引的值，并将其存储在数组中。

我们可以从任何一个索引中取值，以获得斐波那契数列中的相应数字。

**例如：**如果fibNum 是一个存储斐波那契数字的数组，那么我们就插入：

fibNum[0]  = 0 ;  fibNum[1] = 1 ;

然后在一个有指针变量i的迭代循环里面，我们写：

fibNum[i] = fibNum[ i - 1 ] + fibNum[ i - 2 ] ;

源于此。缩放器专题

自下而上方法的算法

首先，你把输入‘n’ ，得到斐波那契数列中的相应数字。

然后，你需要存储斐波那契数列的值，所以你为此声明一个大小为‘n’ 的数组。

接下来，插入前两个索引的值，分别为0 和1 ，。

对第三个和其他剩余的索引使用一个迭代循环，如上面的解释中所述。

最后，返回数组中最后一个索引的值。

自下而上方法的优点

• 更容易创建测试用例。
• 你的代码是可重复使用的
• 由于数据的封装和数据的隐藏，冗余度较低。

自下而上方法的缺点

• 它有时会消耗额外的空间和时间。
• 有时，在最初阶段工作时很难理解。

如何对斐波那契数列进行编码

有多种方法可以在Java中写一个程序来寻找斐波那契数。

1.如何用简单的迭代循环来编码斐波那契数列

下面是如何在Java中使用for循环得到第n个斐波那契数的代码：

import java.util.*;
public class fibonacci{
    public static void main(String args[]){
        int n,k;
        Scanner snr= new Scanner(System.in);
        n=snr.nextInt();
        snr.close();
        int array[]=new int[n];
        // The space used here is O(N)
        array[0]=0;
        array[1]=1;
        for(k=2;k<n;k++)array[k]=array[k-1]+array[k-2];
        // The array is traversed only once so time complexity is O(N)
        System.out.println("Nth number in Fibonacci series is "+array[n-1]);
    }
}

下面是如何在Java中使用while循环得到第n个斐波那契数的代码：

import java.util.*;
public class fibonacci{
    public static void main(String args[]){
        int n,k;
        Scanner snr= new Scanner(System.in);
        n=snr.nextInt();
        snr.close();
        int array[]=new int[n];
        // The space used here is O(N)
        array[0]=0;
        array[1]=1;
        k=2;
        while(k<n)
            array[k]=array[k-1]+array[k-2];
            k++;
        System.out.println("Nth number in Fibonacci series is "+array[n-1]);
    }
    // The array is traversed only once so the time complexity is O(N)
}

时间复杂度

这种方法的时间复杂度是O(N) ，这是线性时间复杂度，因为我们只遍历了一次阵列。

空间复杂度

这种方法的空间复杂度是O(N) ，这是线性的空间复杂度，因为我们把子问题的答案存储在一个数组中。

2.如何使用递归对斐波那契数列进行编码

现在我们来看看在Java中使用递归的斐波那契数列的算法。

在递归中，我们使用一个定义好的函数（假设在这段代码中是fib ）来寻找斐波那契数字。

在main() 函数中，我们为斐波那契数列中的第 n 个数字调用函数fib() 。

我们为这个递归调用定义了基本情况--即它分别为第0个和第1个斐波那契数字返回0 和1 。

我们将像fib( x ) = fib( x-1 ) + fib( x-2) 一样在自身内部调用该函数，直到它达到基数情况，然后我们将从那里获得数值。

如何在Java中使用递归获得第n个斐波那契数的代码

import java.util.*;
public class fibonacci{
    public static void main(String args[]){
        int n;
        Scanner snr= new Scanner(System.in);
        n=snr.nextInt();
        snr.close();
        System.out.println(fib(n)); 
//Printing number in Fibonacci series
    }
    public static int fib(int n){
        if(n==0){
            return 0;
        }
        // Base cases return itself 0 and 1
        else if(n==1){
            return 1;
        }
        else{
            return fib(n-1)+fib(n-2);
            // Recursive calls
        }
    }
}

时间复杂度

这种方法的时间复杂度是O( 2 ^ N ) ，这是指数级的时间复杂度，其中n是第n个斐波那契数的索引。

我们需要找到前两个值来获得每个值。为此，我们为每个值调用两次函数，树最多可以有n 级。

这使得树上有大约2 ^ n 个节点。

空间复杂度

使用递归方法的空间复杂度是O( 2 ^ N ) ，这是指数空间复杂度，其中n是第n个斐波那契数的索引。

由于我们需要存储每个节点的值，并且我们有2 ^ N ，我们需要的总空间是2 ^ N 。

3.如何使用递归和记忆化对斐波那契数列进行编码？

记忆化意味着我们不断地存储所有子问题的解决方案，这样我们就可以在未来的程序中直接检索和使用任何需要它的值。这可以为我们节省时间和空间。

在Java中使用递归进行斐波那契数列的算法

在这里，我们定义了一个函数（我们使用的是fib() ）并使用它来寻找我们想要的斐波那契数。

我们声明一个全局数组，其长度足以存储所有计算后的斐波纳契数。

在main() 函数中，我们为第 n 个数字调用函数fib() 。然后我们为递归调用设置基数，并返回0 和1 ，分别为第0和第1个索引。

我们为所有的x > 2 ，调用fib(x) = fib( x-1 ) + fib( x-2 ) 。对于每一个计算出的值，我们都将其存储在全局数组中。

每个斐波那契数的值都存储在全局索引的相应索引中。然后我们可以检索和使用它们以备后用。这极大地提高了时间的复杂性。

如何在Java中使用递归与记忆化获得第n个斐波那契数的代码

import java.util.*;
public class fibonacci{
    public static int fib(int n){
        if(n==1){
            return array[0];
        }
        // base cases
        if(n==2){
            return array[1];
        }
        else{
            array[n-1] = fib(n-1) + fib(n-2);
            return (array [n-1]);
        }
    }
    public static void main(String args[]){
        int n;
        Scanner snr= new Scanner(System.in);
        n=snr.nextInt();
        snr.close();
        array[0]=0;
        array[1]=1;
        System.out.println(fib(n));
        // printing number in fibonacci series
    }
    static int array[]=new int[1000];
    // Declaring global array large enough
 }

时间复杂度

这种方法的时间复杂度是O( N ) ，这是线性时间复杂度，其中n 是第n个斐波那契数的索引。

我们需要找到前两个值来获取每个值--但在这里我们已经将它们存储在数组中，所以我们只需要对所有元素调用一次函数。

空间复杂度

这种方法的空间复杂度是O( N ) ，这是线性空间复杂度，其中n 是第n个斐波那契数的索引。

我们只需要存储每个节点的值，而且我们只有N个节点。

总结

在这篇文章中，我们学习了如何用四种不同的方法在Java中寻找斐波那契数列，自下而上的方法和自上而下的方法各有两种。

我们还了解到，带有备忘功能的递归是获得斐波那契数的最省时省力的方法。

在这篇文章中，我们讨论了每种方法的空间和时间复杂度，以及它们的算法、优点和缺点。

学习和编码愉快!