和QuickSort一样,合并排序也是一种排序方法,在这种方法中,数组被分成两半,按这两半进行排序。在排序之后,这些半数被合并起来。这个过程是递归的,因为数组的每一半都被再次分成两半,进行排序和合并。
Java中的合并排序
Java合并排序是一种 "分而治之 "的算法,我们首先将问题分成许多子问题。 然后,它 将输入的数组 分成两半,为它们调用自己,然后将这两半排序的数组合并。
merge()函数用于合并这两个半数。因此,用一句话来说,我们可以说,在合并排序中,我们先进行分割操作,然后是征服和合并操作。
当我们有了子问题的解决方案后,我们把它们合并起来,得到一个最终的解决方案。
这是一个简单的算法,可以很容易地使用递归来实现,因为我们处理的是子问题而不是大的主问题。
简而言之,MergeSort算法可以描述为以下两步过程。
- 分割:在这一步中,我们将一个输入数组分成两半,中枢是一个数组的中点。这一步对所有的半数数组递归进行,直到没有更多的半数数组需要划分。
- 征服:在这一步中,我们将被分割的数组从下到上进行排序和合并,得到排序后的数组。
举例说明
在每一个环节中对元素的处理可以理解为以下几点。
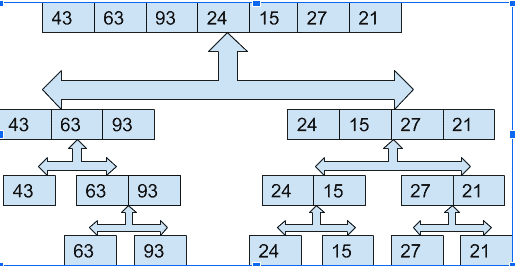
假设我们得到了下面的数组,它需要被排序。
| 43 | 63 | 93 | 24 | 15 | 27 | 21 |
这里,数组的大小是7,所以,我们把它分成两半。由于这里的元素数是奇数,我们的后半部分将比前半部分多一个元素。
| 43 | 63 | 93 | |
| 24 | 15 | 27 | 21 |
现在,这两半将被分类和合并。但这又将以同样的方式发生,即分成两半,进行排序,然后合并。
因此,将遵循以下算法:
int[] Merge_sort(arr[], start, end)
if(end>start):
mid=(start+end)/2
first[]=Merge_sort(arr, start, mid)
second[]=Merge_sort(arr, mid+1, end)
arr[]=Merge( first, second)
return arr[]
| 43 | 63 | 93 | 24 | 15 | 27 | 21 |
所以,在上面的例子中,数组的排序将如下进行:
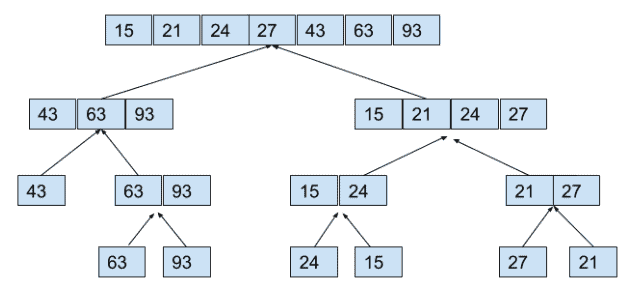
所以,在分割数组并将其分离成一个单元后,我们现在将执行征服操作,在这里将进行排序。 下面的图显示了如何进行征服操作和最终的排序数组:
最后,这两半将被合并:
| 15 | 21 | 24 | 27 | 43 | 63 | 93 |
合并排序的Java程序
Java中合并排序的代码如下:
import java.util.*;
public class MergeSort {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println("Enter the size of the Array: ");
int size_of_arry = sc.nextInt(); // size of array, to b entered by the user
int arr[] = new int[size_of_arry];
System.out.println("Enter Array Elements ");
for (int i = 0; i < size_of_arry; i++)
arr[i] = sc.nextInt(); // element of array, to be entered by the user
arr = Merge_sort(arr, size_of_arry);
System.out.println("Array after Merge Sort is: ");
for (int i = 0; i < size_of_arry; i++)
System.out.print(arr[i] + " ");
System.out.println("\n");
}
static int[] Merge_sort(int arr[], int size) {
if (size > 1) {
int mid = size / 2;
int[] first = Arrays.copyOfRange(arr, 0, mid);
first = Merge_sort(first, mid); // recursive call for first half array
int[] second = Arrays.copyOfRange(arr, mid, size);
second = Merge_sort(second, size - mid); // recursive call for second half array
arr = Merge_arrays(first, second, mid, size - mid);
}
return arr;
}
static int[] Merge_arrays(int first[], int second[], int n, int m) // respectively
{
int arr[] = new int[n + m];
int i = 0, f = 0, s = 0;
while (f < n && s < m) {
if (first[f] < second[s])
arr[i++] = first[f++];
else
arr[i++] = second[s++];
}
while (f < n)
arr[i++] = first[f++];
while (s < m)
arr[i++] = second[s++];
return arr;
}
}
请看下面的例子:
时间复杂度
合并排序算法的时间复杂度是O(n log n)。
该程序代码的时间复杂度在所有情况下都是一样的,即最坏情况或最好情况。
应用
- 合并排序对于在**O(n log n)**时间内对链表进行排序很有用
- 它被用于反转计数问题中
- 我们可以在外部排序中使用它
- 如果发生大量的并行化,那么并行化的Mergesort比其他算法更直接
- 当你需要稳定排序时,你可以使用合并排序。这是合并排序的一个基本特征
- 当对不适合内存的文件进行排序时,你可能会把它分成适合内存的小块,使用独立的方式对这些进行排序,把每一个写到文件中,然后对生成的文件进行合并排序
本教程就到此为止。