在这篇文章中,我们提出了一种算法来检查给定井字形配置的输赢。
注意:这个算法假定游戏数据是以以下格式传递的
data = [
# the lists are rows while the individual dictionaries are tiles (the move made and the tile number)
[
{'move': 'x', 'number': 1},
{'move': 'o', 'number': 2},
{'move': 'x', 'number': 3}
],
[
{'move': 'x', 'number': 4},
{'move': 'o', 'number': 5},
{'move': 'o', 'number': 6}
],
[
{'move': 'x', 'number': 7},
{'move': 'x', 'number': 8},
{'move': 'x', 'number': 9}
]
]
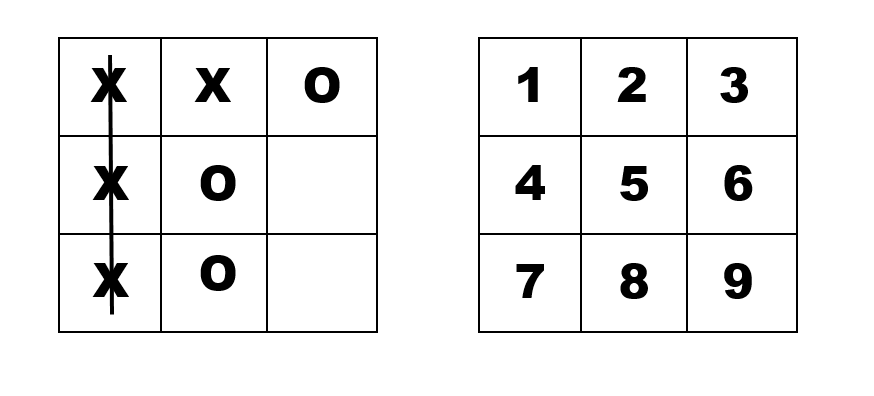
为什么采用上述格式?看看下面的图片吧
从上面的图片中,我们可以看到有一个大块,就像容器一样,我们有行(水平方向从左到右的块)和列(垂直方向从上到下的块),每行有3个小块或瓷砖。
在我们上面的代码中,我们有同样的结构。
- 我们有一个列表(命名为data),它就像一个容器。
- 在 "容器列表 "中的其他3个列表代表了3行。
- 在每一行中,我们有一个瓦片,它被表示为python字典。为什么呢?这是因为我们需要跟踪移动和移动所处的瓷砖编号。
现在,让我们来谈谈算法的实现
对于这个例子,我们将把X
作为我们的 "胜利 "之举(为了使事情更简单)
第1步:什么算作是赢?
- 如果同一步棋横跨(水平方向)在一行上,即
[1,2,3]、[4,5,6]、[7,8,9],都是同一步棋。这是最简单的实现。 - 如果同一步棋在垂直方向上跨越一列,即
[1,4,7]或[2,5,8]或[3,6,9]都是同一步棋。 - 如果同一步棋沿对角线跨过对局,那就是
[1,5,9]或[3,5,7]。注意:永远只有两个数字。
第2步:如何计算第1.1步的胜负:同一步棋横跨(水平方向)在一行上
# assuming we are checking for the move x
data = [
[{'move': 'x', 'number': 1}, {'move': 'x', 'number': 2}, {'move': 'o', 'number': 3}], [{'move': 'o', 'number': 4}, {'move': 'o', 'number': 5}, {'move': 'x', 'number': 6}], [{'move': 'x', 'number': 7}, {'move': 'x', 'number': 8}, {'move': 'x', 'number': 9}]
]
def row_win(row):
for tile in row:
if tile['move'] != 'x':
return False
现在就这样了,这也将成为计算其他胜利的基础(继续阅读,你会明白为什么)。
这里我们有一个叫做row_win 的函数,它检查是否有除'x'以外的任何其他棋步,如果有,就意味着胜利的条件被违反了,因此所检查的行没有胜利。
我们用它来检查所有的行,如果返回除False 以外的任何其他值,就有胜利。
要检查所有行的胜利
for row in game:
if row_win(row) != False:
return 'x wins!'
第3步:如何计算1.2的胜率:同一步棋沿着一列垂直横行
现在事情变得有趣了,你会明白为什么我选择了这样的数据结构。
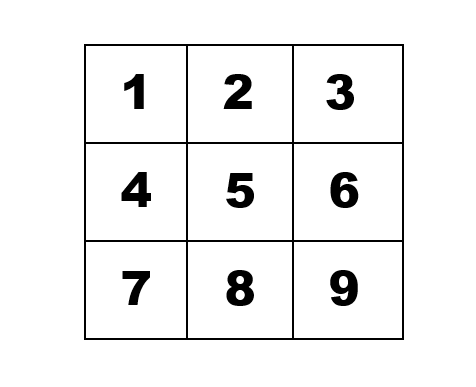
如果你回头看看我给瓷砖编号的图片。
你可以清楚地看到,第一行包含数字1、2和3,或者作为一个列表[1,2,3] ,其他行也是如此。
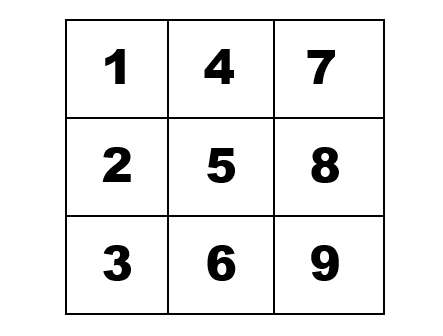
但是,再次看一下这一列,只是第一列。它包含瓷砖1、4和7,或者作为一个列表[1,4,7] 。因此,我们要做的是找到一种方法,将这些元素组合在一起,形成与我们的数据相同的结构,但看起来像这样。
让我们从这个角度看一下。
[[1,2,3], [4,5,6], [7,8,9]]
现在,这些元素都排成了队,我想它更清楚了。我们很幸运,Python提供了一个内置的函数,叫做zip() ,它几乎可以为我们做这些事情。就像这样!
vertical_list = list(zip(*data))
就是这样!zip() 函数返回一个zip 对象,当你对它进行迭代时,它会产生每个值。我们使用list()
将其转换为一个列表
现在,为了计算所有行,我们使用与第2
步
相同的函数
for row in vertical_list:
if row_win(row) != False:
return 'x wins!'
第4步:如何计算第3局的胜利:同一步棋横跨对角线的棋局
同样,我们需要找到一种方法来过滤掉形成对角线的棋局的数值。这就是[1,5,9] 和[3,5,7] 。
与上次不同的是,我们没有一个内置的函数,但要实现一个可以为我们做的函数非常容易。
让我们先想想我们要做什么,然后再看看我们如何做。
data = [
[1,2,3],
[4,5,6],
[7,8,9]
]
我们想从第一个列表中获得第一个元素,从第二个列表中获得第二个元素,从第三个列表中获得第三个元素。现在这就是我所说的清晰的模式。
我们必须得到这个[data[0][0], data[1][1], data[2][2]]
,
记住
阵列的索引从0开始。
output = []
count = 0
for i in range(0, len(lst)):
for _ in lst[i]: # we use _ because we don't need to store the item as a variable. its a "throw away" variable.
output.append(lst[i][count])
count += 1
让我们来分析一下这段代码
这段代码的输出将是一个列表,也就是一个对角线。我们创建一个空的列表output = [] ,我们将在其中存储我们的值(瓦片)。
然后我们在行中循环,对于每一行,我们得到比前一行多一步的瓦片。
range(0, len(lst)) 我们将返回0到2,总共是3。
然后我们循环浏览每张瓷砖,并将 ,输出列表中的值为append
lst[i][count]
我们用0的值初始化了count 这个变量。只有当一行中的所有项目/瓦片都被遍历,并且所需的瓦片被追加到输出列表中后,我们才将其递增1。
但问题就出在这里,在第二个循环中,也就是内循环。它运行的次数与我们行中的项目/瓷砖的数量一样多,也就是3个。每一次,它都存储一个值,也就是lst[0][0] ,与第一行一样。这是因为直到内循环结束后,count变量才会被递增。
所以,我们最终会出现重复的结果。一个看起来像这样的输出列表
output = [1,1,1,5,5,5,9,9,9]
如果我们的列表和上面的一样简单,只有数字,我们可以这样做
list(set(output))
theset 是一个不允许重复对象的数据结构。在 python 中,你可以用以下方法创建一个新的集合set()
但只有一点,你不能用字典的列表来做这个。为什么呢?字典是不可哈希的。
这是什么意思呢?这就是今天的挑战。
总之,要使dict 对象具有哈希性,关键是使用.item() 方法。它返回一个对象的元组。
tuple 是一个不可变的
对象,意味着它的值永远不会改变。
output = []
count = 0
for i in range(0, len(lst)):
seen = set() # create a new set instance
for item in lst[i]: # loops through each item in the row
t = tuple(lst[i][count].items()) # create a tuple, immutable, from each tile which is a dict object
if t not in seen: # checks if the tuple which is the tile is not in the set
seen.add(t) # adds to the set
output.append(lst[i][count]) # adds to the ouput list
count += 1
如果我要解释散列和不可变性的概念,那么这将变得非常大,所以我继续前进并找到了一个非常好的解释。
但请记住,我们有两个对角线,那么我们如何获得另一个对角线呢,我直接说吧,我们只需要反转或逆转瓷砖:
Original:
---------------|
1 | 2 | 3 |
---------------|
4 | 5 | 6 |
---------------|
7 | 8 | 9 |
---------------|
Reversed:
---------------|
3 | 2 | 1 |
---------------|
6 | 5 | 4 |
---------------|
9 | 8 | 7 |
---------------|
有了反转的瓷砖或结构,我们就可以用得到第一个对角线的同样方法轻松得到另一条对角线。感谢Python,我们有另一个内置的叫做revsered() ,它返回一个list_reverseiterator object 。因此我们可以做这样的事情。
reversed_data = []
for row in data:
reversed_game_lst.append(list(reversed(row)))
现在我们已经有了获得垂直列表和水平列表的代码,为了计算胜负,我们只需使用第1步的代码
,把它们打包成函数,让它接受棋步和对局数据作为参数:
def row_win(row, move):
for tile in row:
if tile['move'] != move:
return False # no win in this row!
# if it returns anything other than False, it is a win.
def get_diagonal_lst(lst):
output = []
count = 0
for i in range(0, len(lst)):
seen = set()
for _ in lst[i]: # unused variable represented as '_'
t = tuple(lst[i][count].items())
if t not in seen:
seen.add(t)
output.append(lst[i][count])
count += 1
return output
# 1
def horizontal_win(game, move):
for row in game:
if row_win(row, move) != False:
return True # there is a win!
# 2
def vertical_win(data, move):
tilted = list(zip(*data))
for row in tilted:
if row_win(row, move) != False:
return True # there is a win!
# 3
def diagonal_win(data, move):
reversed_data = []
for row in data:
reversed_data.append(list(reversed(row)))
d_lst = [get_diagonal_lst(data), get_diagonal_lst(reversed_data)]
for row in d_lst:
if row_win(row, move) != False:
return True # there is a win!
def check_for_win(data, move):
if horizontal_win(data, move) or vertical_win(data, move) or diagonal_win(data, move):
print(f'{move} wins')
else:
print(f'no win for {move}')
# or you could return what you want
让我们试试吧,我做了一个简单的方法来获取输入(我们假设是游戏):
game = []
for i in range(1, 10):
move = input('enter your move [x or o]: ')
game.append({'move': move, 'number': i})
# divide game into 3 lists (rows)
game = [ game[0:3],
game[3:6],
game[6:9]
]
check_for_win(game, 'x')
check_for_win(game, 'o')
这将接受9个输入,也就是9个棋子,并将数据的格式化,使其符合我们想要的结构。
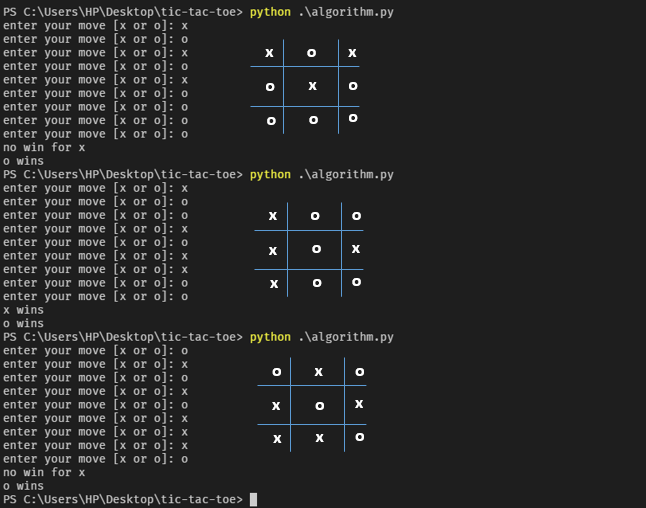
这是一个输出样本。
现在,有些人或每个人都可能会看一看,然后说,等一下,所有的牌都被使用了,或者X和O都赢了!这就是为什么这个算法应该被称为 "X"。这就是为什么这个算法应该用于计算任何棋手下棋后的胜利。这是对你的另一个挑战,实现它。
谢谢大家的阅读 :)