掉蛋之谜的算法介绍

在这篇文章中，我们用包括组合学和动态编程在内的各种算法深入探讨了掉蛋之谜。

目录

I.对问题的介绍
II.2个鸡蛋k个楼层
III.N个鸡蛋k层
3.1 使用组合学
3.1.1 自上而下的方法
3.1.2 自下而上的方法
3.2 使用动态编程
3.2.1 自上而下的方法
3.2.2 自下而上的方法

I.对问题的介绍

丢蛋之谜代表了一个问题，即在尽可能少的资源和尝试的情况下，找到测试从某个楼层丢蛋的最佳方法。

在现实中，鸡蛋是非常脆弱的，所以从你的手中掉下来会变得非常恶心:)

那么，你将如何测试从10层楼掉落1个鸡蛋，或从100层楼掉落2个鸡蛋，或从k层楼掉落N个鸡蛋？

在第一种情况下，你可以尝试从第一层楼掉下来，然后继续到第十层楼。这将是一个复杂度为O(n)的线性方法。
不如先从5楼开始尝试，如果它破了，那么你就会知道如果你从以上楼层扔下它，它肯定会破，但你不知道从哪个低级楼层扔下是安全的，因为你没有任何其他鸡蛋可以测试。
如果它没有破，那么你可以继续从7楼，也就是未测试楼层的一半，以此类推。
你可以意识到，对于一个鸡蛋，这种测试方法不是一个好方法，所以你可能考虑增加一个鸡蛋。

II.2个鸡蛋K楼层

对于2个鸡蛋，你可以尝试之前的策略，但同样，在某些时候，它可能会再次破裂，而你没有其他鸡蛋可以测试，尤其是当楼层数增加到100层的时候！
如果改变策略，从指定楼层开始投下第一个鸡蛋，如果它破裂，第二个鸡蛋将覆盖它后面所有未测试的楼层呢？
在这种情况下，如果第一个鸡蛋在k层打碎了，你将有第二次机会用第二个鸡蛋去检查剩下的k-1层，总的尝试次数为(x-1)+1，也就是x，其中x-1是在之前的尝试安全完成后从k-1层掉下来的鸡蛋，1是在k层的尝试。

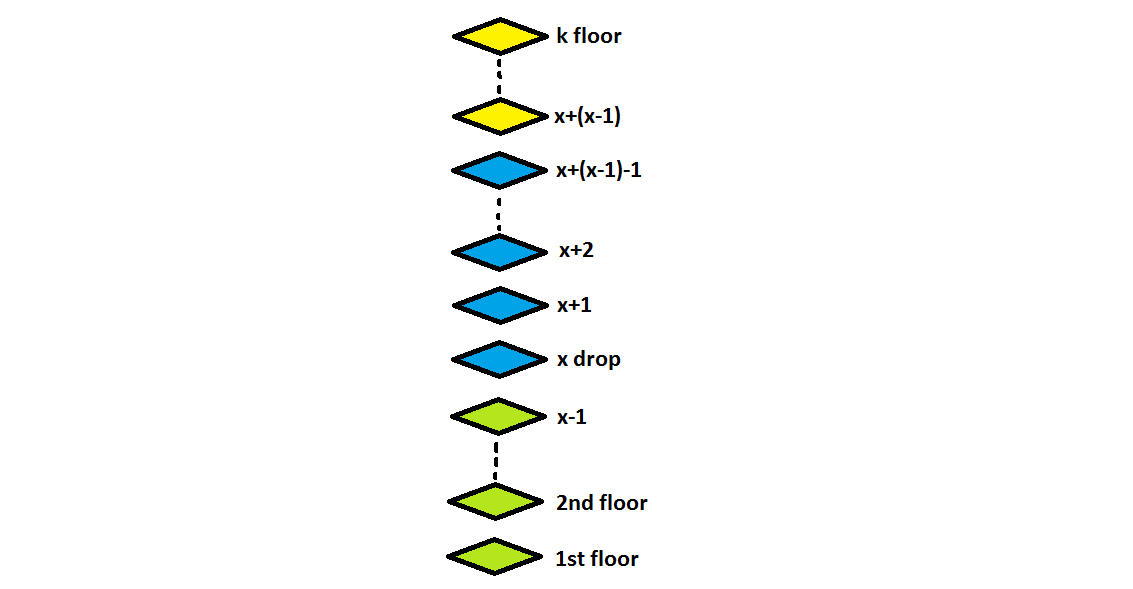
这将导致我们在任何时候都能覆盖固定数量的楼层，这可以通过下一个公式进行数学转换。

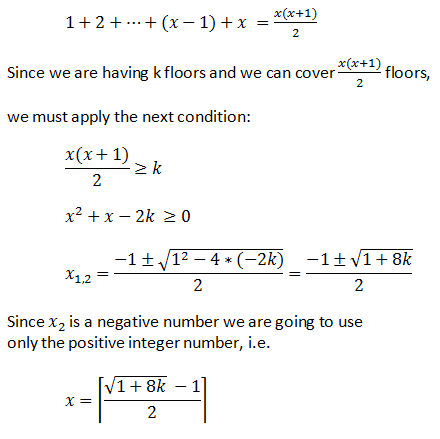
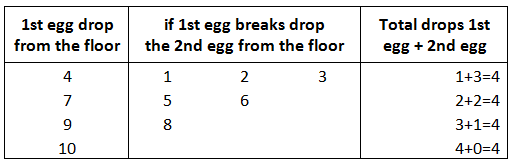
如果是10层楼，x = 4滴。

如果是100层楼，x = 13.65 = 14滴

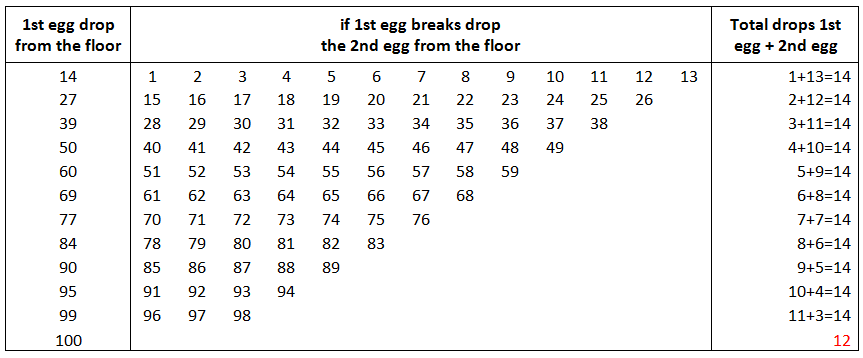
注意第一个鸡蛋的总尝试次数，小于14次，因此因为x的模数2不同于0 !

上述逻辑可以转化为下一个C++程序:

    #include <iostream>
    #include <math.h>

    using namespace std;

    int main()
    {
        int i=0,j=0,l=1;
        int k=108;
        double f=(sqrt(8*k+1)-1) / 2.0;
        int x = (int)(f+0.9); //round up the number of floors

        for (i=x; i<=k && l<=x; i+=x-l++ )
            {
                cout<<i<<endl;
                for (j=i-(x-l); j<i; j++)
                    cout<<" "<<j;
                cout<<endl;
            }
        //next for is used to cover the untested floors for the 1st egg    
        for (i=i-(x-l); i<=k; i++ )
            cout<<i<<endl;
        return 0;
    }

输出为k=108。

    15
     1 2 3 4 5 6 7 8 9 10 11 12 13 14
    29
     16 17 18 19 20 21 22 23 24 25 26 27 28
    42
     30 31 32 33 34 35 36 37 38 39 40 41
    54
     43 44 45 46 47 48 49 50 51 52 53
    65
     55 56 57 58 59 60 61 62 63 64
    75
     66 67 68 69 70 71 72 73 74
    84
     76 77 78 79 80 81 82 83
    92
     85 86 87 88 89 90 91
    99
     93 94 95 96 97 98
    105
     100 101 102 103 104
    106
    107
    108

III.N个鸡蛋 k层

3.1 使用组合学

上述解决方案可以用组合学来写，并扩展到一般情况下。

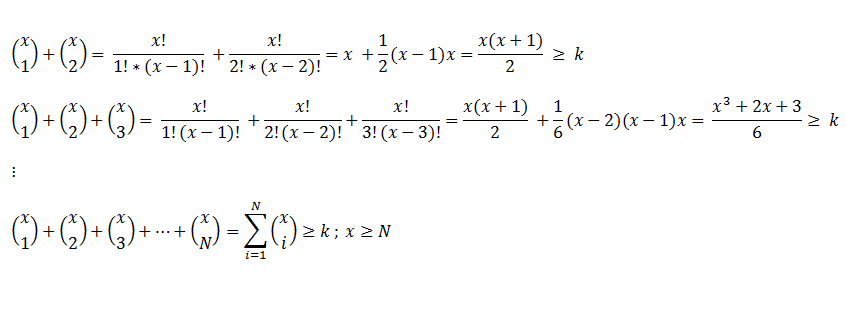
如果鸡蛋的数量N大于尝试的数量x，那么就需要增加一个最小化的条件。

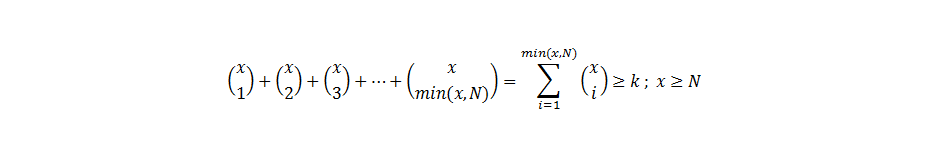
当你看到所有这些方程时，情况相当复杂，但事实上，如果我们要应用组合的递归特性，这在编程时将很容易实现。

基本上，我们需要做的是确定第一个x，或最小的尝试次数，当组合之和大于或等于楼层数时。

我们可以使用线性搜索或二进制搜索算法来找到x

• 在线性搜索的情况下是O(n)
• 在二进制搜索的情况下是O(log n)

在这些算法中，将增加确定组合的时间执行，其中

• 在组合函数的情况下是O(2^n)
• 在sum_comb函数的情况下是O(n)

    #include <iostream>
    #include <bits/stdc++.h>
    #include <chrono>

    using namespace std;

    int comb (int attemps, int eggs)
    {
      if (eggs == 0 || attemps == eggs)
        return 1;
      return comb (attemps - 1, eggs) + comb (attemps - 1, eggs - 1);
    }

    int sum_comb (int attemps, int eggs)
    {
      long long unsigned int sum = 0;
      
      if(attemps < eggs) eggs = attemps;

      for (int i = 1; i <= eggs; i++)
        sum += comb (attemps, i);

      return sum;
    }

    int linear_search (int eggs, int floors)
    {
      int attemps, sum=0, i = 1;

      while ( sum < floors)  
        {
            sum = sum_comb(i,eggs);
            attemps = i++;
        };

      return attemps;
    }
    
    int binary_search (int eggs, int floors)
    { int sum ;
      int limit_inf = 1;
      int limit_sup = floors;
      int mid ;

      while (limit_inf <= limit_sup)
        {
            mid = (limit_inf + limit_sup) / 2.0;
            sum = sum_comb(mid,eggs);
            if(sum < floors)
                limit_inf = mid + 1;
            else if(sum > floors) 
                    limit_sup = mid - 1;
                 else
                    return mid;
        }
        return mid;
    }
    int main ()
    {
      double time_taken;
      
      int N=2, k=100;  
      
      auto start = chrono::high_resolution_clock::now();
      ios_base::sync_with_stdio(false);
      cout <<"linear search: "<< linear_search (N, k)<<endl;
      auto end = chrono::high_resolution_clock::now();
      time_taken = chrono::duration_cast<chrono::nanoseconds>(end - start).count();
      time_taken *= 1e-9;
      cout << "Time taken by linear search is : " << fixed 
             << time_taken << setprecision(6)<< " sec" << endl;
      
      start = chrono::high_resolution_clock::now();
      ios_base::sync_with_stdio(false);
      cout <<"binary search: "<< binary_search (N, k)<<endl;
      end = chrono::high_resolution_clock::now();
      time_taken = chrono::duration_cast<chrono::nanoseconds>(end - start).count();
      time_taken *= 1e-9;
      cout << "Time taken by binary search is : " << fixed 
             << time_taken << setprecision(6)<< " sec" << endl;
      
      return 0;
    }

输出:

线性搜索。14
线性搜索花费的时间是：0.000065秒
二进制搜索。14
二元搜索耗时：0.000025秒

3.1.1 自上而下的方法

我们在前面看到了如何使用组合的递归定义来生成解决方案。
我们可以改进之前的程序吗？

二元搜索已经被优化，组合的总和只是一个简单的和，所以唯一需要改进的代码是梳子函数。
因为我们是利用它们的递归特性进行计算，所以多次调用函数会导致多次调用同一个函数得到相同的结果。
接下来的例子说明了这一点：

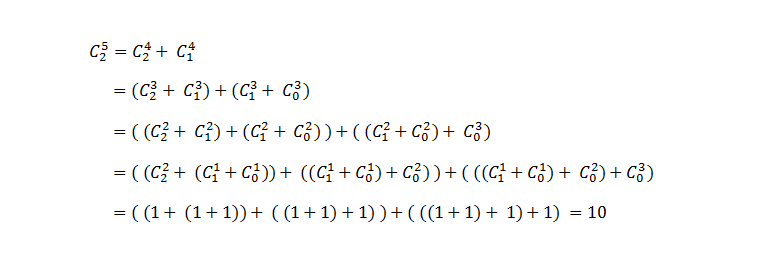
我们能不能改进一下？

如果在调用函数后保存之前的结果，并在其他调用中只引用该值，那会怎么样？这种技术被称为 "记忆化"（memoization），意思是我们首先将问题分割成子问题，然后计算并存储结果。

注意：由于我们是从1开始的，而且为了简化学习，矩阵中的第一列不被使用。

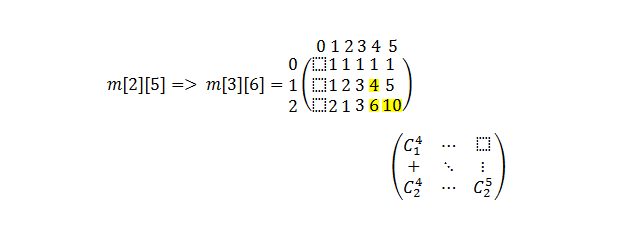
    #include <iostream>
    #include <bits/stdc++.h>
    #include <chrono>

    using namespace std;

    int **m;

    void init (int N, int k)
    {
        int i;

        //dynamically memory allocation
        m = new int* [N+1];
        for (i=0;i<k+1;i++)
            m[i] = new int[k+1]; 

        //matrix initialization
        for (i=1; i<= k; i++)
            {
                m[0][i] = 1;
                if (i<=N) m[i][i] = 1;
            }
    }

    int comb_memoization (int N, int k)
    {
        if (m[N][k] != 1)
            m[N][k] = comb_memoization(N-1,k-1) + comb_memoization(N,k-1) ;

        return m[N][k];                        
    }

    int sum_comb (int attemps, int eggs)
    {
      int sum = 0;

      if(attemps < eggs) eggs = attemps;

      for (int i = 1; i <= eggs; i++)
        sum += comb_memoization (i, attemps);

      return sum;
    }

    int linear_search (int eggs, int floors)
    {
      int attemps, sum=0, i = 1;

      while ( sum < floors)  
        {
            sum = sum_comb(i,eggs);
            attemps = i++;
        };

      return attemps;
    }

    int binary_search (int eggs, int floors)
    { int sum ;
      int limit_inf = 1;
      int limit_sup = floors;
      int mid ;

      while (limit_inf <= limit_sup)
        {
            mid = (limit_inf + limit_sup) / 2.0;
            sum = sum_comb(mid,eggs);
            if(sum < floors)
                limit_inf = mid + 1;
            else if(sum > floors) 
                    limit_sup = mid - 1;
                 else
                    return mid;
        }
        return mid;
    }
    int main ()
    {

      double time_taken;

      int N=2, k=100;  

      init(N,k);

      auto start = chrono::high_resolution_clock::now();
      ios_base::sync_with_stdio(false);
      cout <<"linear search: "<< linear_search (N, k)<<endl;
      auto end = chrono::high_resolution_clock::now();
      time_taken = chrono::duration_cast<chrono::nanoseconds>(end - start).count();
      time_taken *= 1e-9;
      cout << "Time taken by linear search is : " << fixed 
             << time_taken << setprecision(6)<< " sec" << endl;

      start = chrono::high_resolution_clock::now();
      ios_base::sync_with_stdio(false);
      cout <<"binary search: "<< binary_search (N, k)<<endl;
      end = chrono::high_resolution_clock::now();
      time_taken = chrono::duration_cast<chrono::nanoseconds>(end - start).count();
      time_taken *= 1e-9;
      cout << "Time taken by binary search is : " << fixed 
             << time_taken << setprecision(6)<< " sec" << endl;

      return 0;
    }

输出:

线性搜索。14
线性搜索花费的时间是：0.000055秒
二进制搜索。14
二元搜索耗时：0.000032秒

3.1.2 自下而上的方法

自上而下的方法使用递归公式计算组合，它需要多花一点时间来得到结果。我们可能会想到使用阶乘公式来计算组合，但在这种情况下，会有很多乘法要计算。

如果使用Pascal三角逻辑，从下往上计算组合，而不使用递归呢？这种方式，我们使用了组合的递归定义，但没有在编程中实现。
这种技术被称为制表法
。

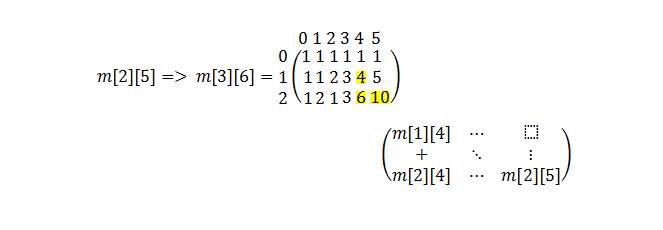
这将使我们的执行时间达到O(n^2)

下面的代码就是这样做的:

    #include <iostream>
    #include <bits/stdc++.h>
    #include <chrono>

    using namespace std;

    int **m;

    void init (int N, int k)
    {
        int i;
        
        //dynamically memory allocation
        m = new int* [N+1];
        for (i=0;i<k+1;i++)
            m[i] = new int[k+1]; 
        
        //matrix initialization
        for(int i=0; i<=N; i++)
            for (int j=0; j<=k; j++)
            {
                m[i][j] = 0;
                m[0][j] = 1;
                m[i][0] = 1;
                m[i][i] = 1;
            }
    }
    
    int comb_tabulation (int N, int k)
    {
        for(int i=1; i<=N; i++)
            for (int j=1; j<=k; j++)
                {
                if (m[i][j] != 1)
                    m[i][j] = m[i-1][j-1] + m[i][j-1] ;
               }
    return m[N][k];                        
    }
    
    int sum_comb (int attemps, int eggs)
    {
      long long unsigned int sum = 0;
      
      if(attemps < eggs) eggs = attemps;

      for (int i = 1; i <= eggs; i++)
        sum += comb_tabulation (i, attemps);

      return sum;
    }

    int linear_search (int eggs, int floors)
    {
      int attemps, sum=0, i = 1;

      while ( sum < floors)  
        {
            sum = sum_comb(i,eggs);
            attemps = i++;
        };

      return attemps;
    }
    
    int binary_search (int eggs, int floors)
    { int sum ;
      int limit_inf = 1;
      int limit_sup = floors;
      int mid ;

      while (limit_inf <= limit_sup)
        {
            mid = (limit_inf + limit_sup) / 2.0;
            sum = sum_comb(mid,eggs);
            if(sum < floors)
                limit_inf = mid + 1;
            else if(sum > floors) 
                    limit_sup = mid - 1;
                 else
                    return mid;
        }
        return mid;
    }
    
    int main ()
    {
      double time_taken;
      
      int N=2, k=100;  
      
      init(N,k);
      
      auto start = chrono::high_resolution_clock::now();
      ios_base::sync_with_stdio(false);
      cout <<"linear search: "<< linear_search (N, k)<<endl;
      auto end = chrono::high_resolution_clock::now();
      time_taken = chrono::duration_cast<chrono::nanoseconds>(end - start).count();
      time_taken *= 1e-9;
      cout << "Time taken by linear search is : " << fixed 
             << time_taken << setprecision(6)<< " sec" << endl;
      
      start = chrono::high_resolution_clock::now();
      ios_base::sync_with_stdio(false);
      cout <<"binary search: "<< binary_search (N, k)<<endl;
      end = chrono::high_resolution_clock::now();
      time_taken = chrono::duration_cast<chrono::nanoseconds>(end - start).count();
      time_taken *= 1e-9;
      cout << "Time taken by binary search is : " << fixed 
             << time_taken << setprecision(6)<< " sec" << endl;
      
      return 0;
    }

输出:

线性搜索。14
线性搜索花费的时间是：0.000052秒
二进制搜索。14
二进制搜索耗时：0.000004秒

3.2 使用动态编程

简而言之，动态编程指的是确定一个函数方程，使我们的问题从最初的解决状态向最优状态发展。

让我们把第n个待测蛋和第p个待测地板命名为s(n,p)，其中：
n = 0,1,2,..., N-1
p = 0,1,2,..., k-1

过程的初始状态是s = (N,k)，其中N表示实验开始时可用的测试蛋的数量。当没有更多的试验蛋（n=0）或p=0时，该过程就会终止，以先发生者为准。如果终止发生在状态s=(0,p)且p>0时，则试验失败。

现在，让W(n,p)=在最坏情况下确定临界底线值所需的最小试验次数，给定过程处于状态s = (n,p)。 (1)

然后，可以证明。

W(n,p) = 1 + min{ max( W(n-1, x-1), W(n, p-x) ); x = 1,2,...,p }。

有W(n,0)=0，对于所有n>0，W(1,p)=p，对于所有p>0 (2) (3)

w(2,5)=3的例子

注意每种颜色的执行次数。

这将使我们的执行时间为O(2^n)

接下来的代码会这样做，但会非常慢:

    #include <iostream>
    #include <limits.h>
    #include <bits/stdc++.h>
    #include <chrono>

    using namespace std;

    int w(int n, int p)
    {
        if (p==0)  return 0;
        if (n==1)  return p;

        int minimum=INT_MAX;

        for (int x = 1; x<=p; x++)
            minimum = min(minimum, max(w(n-1,x-1), w(n,p-x))) ; 

        return 1 + minimum;
    }

    int main()
    {
      double time_taken;
      
      int N=2, k=100;  
      
      auto start = chrono::high_resolution_clock::now();
      ios_base::sync_with_stdio(false);
      cout <<"DP top-down: "<< w (N, k)<<endl;
      auto end = chrono::high_resolution_clock::now();
      time_taken = chrono::duration_cast<chrono::nanoseconds>(end - start).count();
      time_taken *= 1e-9;
      cout << "Time taken by DP top-down is : " << fixed 
             << time_taken << setprecision(6)<< " sec" << endl;

        return 0;
    }

输出:

被杀

注意：你可以从输出中看到，我们的测试编译器因为执行时间过长而杀死了这个进程。你可以用另一个参数w(2,10)来运行它，看看它的输出，或者如果你希望在本地运行它，你可能有机会在得到结果之前打个盹。

3.2.1 自上而下的方法

为了改进DP递归，我们可以再次调用记忆化技术，将计算值以矩阵形式存储起来。

下一个程序将这样做:

    #include <iostream>
    #include <limits.h>
    #include <bits/stdc++.h>
    #include <chrono>

    using namespace std;

    int **m;

    void init (int N, int k)
    {
        int i,j;

        //dynamically memory allocation
        m = new int* [N+1];
        for (i=0;i<k+1;i++)
            m[i] = new int[k+1]; 

        //matrix initialization
        for(int i=0; i<=N; i++)
            for (int j=0; j<=k; j++)
            {
                m[i][j] = INT_MAX;
                m[i][0] = 0;
                m[1][j] = j;
            }
    }
    
    int w(int n, int p)
    {
        /*
        // v1 testing condition
        if (p == 0 ) return m[n][p];
        if (n == 1 ) return m[n][p];
        if (m[n][p] != INT_MAX) return m[n][p];
        
        // v2 testing condition
        if (m[n][p] == 0 || m[n][p] == 1 || m[n][p] != INT_MAX) return m[n][p];
        */
        
        // v3 testing condition
        if (p == 0 || n == 1 || m[n][p] != INT_MAX) return m[n][p];

        for (int x = 1; x<=p; x++)
            m[n][p] = min(m[n][p], max(w(n-1,x-1), w(n,p-x))) ;
        
        m[n][p] = m[n][p] + 1;    
        
        return m[n][p];
    }

    int main()
    {
      double time_taken;
      
      int N=2, k=100;  
      
      init(N,k);
      
      auto start = chrono::high_resolution_clock::now();
      ios_base::sync_with_stdio(false);
      cout <<"DP top-down: "<< w (N, k)<<endl;
      auto end = chrono::high_resolution_clock::now();
      time_taken = chrono::duration_cast<chrono::nanoseconds>(end - start).count();
      time_taken *= 1e-9;
      cout << "Time taken by DP top-down is : " << fixed 
             << time_taken << setprecision(6)<< " sec" << endl;

        return 0;
    }

输出:

DP自上而下。14
DP自上而下花费的时间是：0.000190秒

注意在返回数值之前，单元格*m[n][k]*的增量。

另外，你认为哪个版本（1，2或3）的测试条件会很快？, 并不是说这在某种程度上会很重要。

3.2.2 自下而上的方法

由于前面的方法很慢，也许我们可以改进它。
同样，使用一个附加数组来存储以前的结果，将是一个很好的技术。
问题是：如何将函数方程转化为矩阵确定？
因为我们不会以递归的方式调用函数，增量需要在分配之前完成。

m[n][p] = min{ 1 + max( m[n-1][ x-1], m[n][p-x] ) ; x = 1,2,...,p }

有：
m[n][0] = 0 对于所有n > 0
m[1][p] = p 对于所有p > 0
m[0][p] = 0 对于所有p > 0
m[n][1] = 1 对于所有n > 0

w(2,5)=3的例子

这将使我们的执行时间为O(n^3)

接下来的代码将这样做:

    #include <iostream>
    #include <limits.h>
    #include <bits/stdc++.h>
    #include <chrono>

    using namespace std;

    int **m;

    void init (int N, int k)
    {
        int i,j;

        //dynamically memory allocation
        m = new int* [N+1];
        for (i=0;i<k+1;i++)
            m[i] = new int[k+1]; 

        //matrix initialization
        for(int i=0; i<=N; i++)
            for (int j=0; j<=k; j++)
            {
                m[i][j] = INT_MAX;
                m[i][0] = 0;
                m[0][j] = 0;
                m[i][1] = 1;
                m[1][j] = j;
            }
    }

    void print (int N, int k)
    {

        for(int i=0; i<=N; i++)
            {
            for (int j=0; j<=k; j++)
                cout<<m[i][j]<<" ";
            cout<<endl;    
            }
    }
    int w (int N, int k)
    {
         for(int i=2; i<=N; i++)
            for (int j=1; j<=k; j++)
                for(int x=1; x<=j; x++)
                    m[i][j] = min( m[i][j], 1+ max( m[i-1][x-1], m[i][j-x] ));

        return m[N][k];                        
    }

    int main()
    {
      double time_taken;
      
      int N=2, k=100;  
      
      init(N,k);

      auto start = chrono::high_resolution_clock::now();
      ios_base::sync_with_stdio(false);
      cout <<"DP bottom-up: "<< w (N, k)<<endl;
      auto end = chrono::high_resolution_clock::now();
      time_taken = chrono::duration_cast<chrono::nanoseconds>(end - start).count();
      time_taken *= 1e-9;
      cout << "Time taken by DP bottom-up is : " << fixed 
             << time_taken << setprecision(6)<< " sec" << endl;

        return 0;
    }

输出:

DP自下而上。14
DP自下而上花费的时间是：0.000159秒

结论

研究多种方法来找到一个好的算法来解决一个问题，在应用于生产时可能会有很大的影响。

从上述方法中，我们可以注意到，在这种情况下，最佳的时间解决方案是自下而上的组合方法。