什么是Trie？

Trie是一种特殊的数据结构，用于以有效的方式存储数据（一般来说，我们存储字符串）。它类似于树。它是一个n次方树，其中每个分支由n个组件组成。它也被称为前缀树或数字树。它由节点和边组成。它是一种索引结构，经常用于信息检索和组织。

它被用于字典中（存储、删除、搜索），寻找前缀字符串。它是一种有序的数据结构。

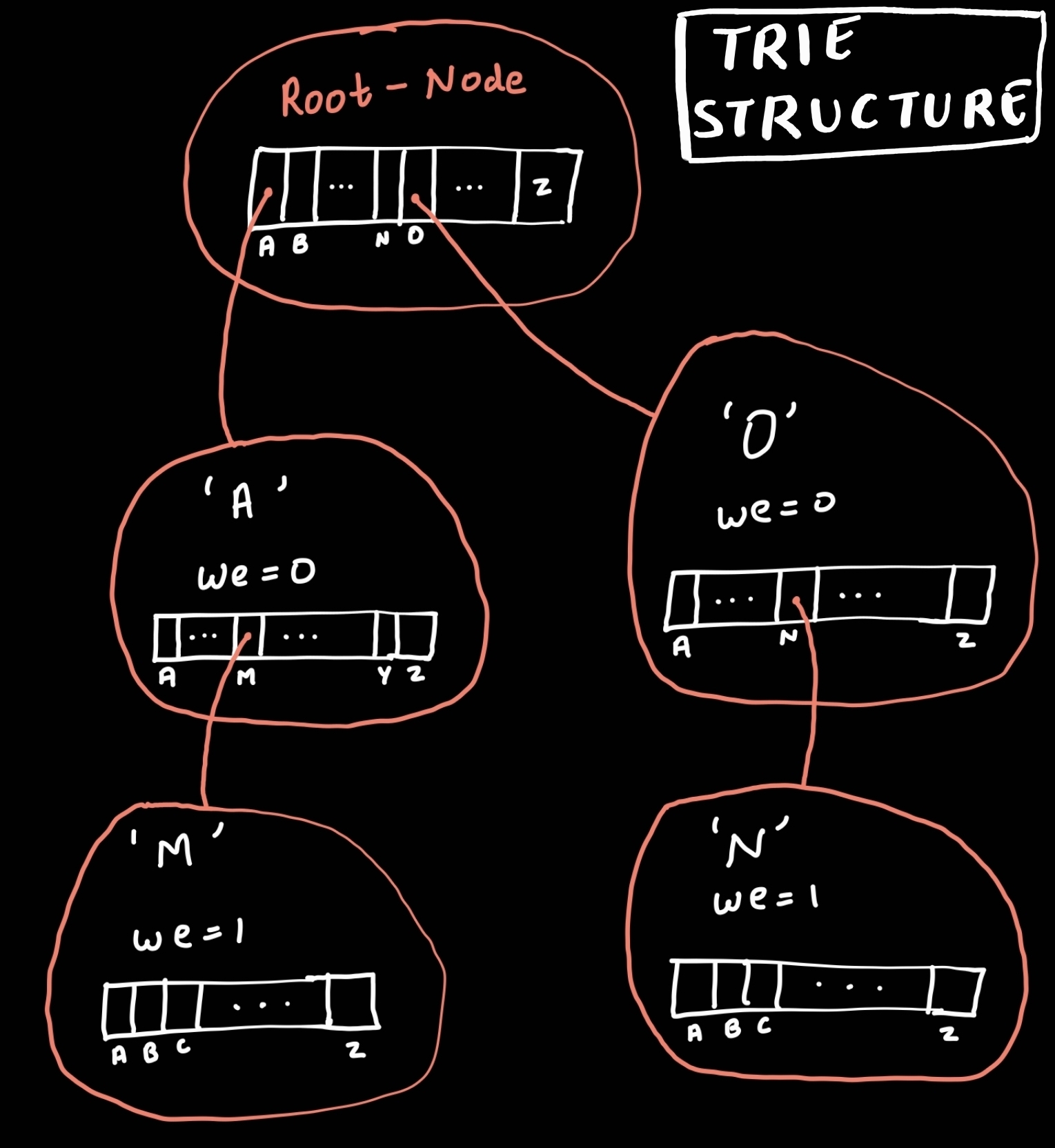
Trie数据结构的结构

struct trie-node{
    trie-node *child[26];        //26 because english have 26 alphabets
    //child will have 26 values
    bool we;        //"we" stands for end of word
};

"我们 "将告诉你这个字母是否是单词的结尾？
对于单词的最后一个字母，"我们 "将有1（1）或True，其余的字母有0（0）或False。
trie的数据结构如下图所示

三元组的自下而上的遍历

三元组自下而上的遍历是一种以从下到上的方式打印字母的方法。这是一个递归法。
例如。让我们把{ cat, coa, bat, bar, on }存储在Trie中。Trie看起来就像下面给出的那样：

Trie:
       Root-Node
    /      |      \
   b       c       o
   |      / \      |
   a     a   o     n
  / \    |   |
 r   t   t   a

现在，在打印时，我们将首先以自下而上的方式打印最左边的子树，然后以自下而上的方式打印第二个最左边的子树，然后以同样的方式打印第三个最左边的子树，最后到最右边的子树。
在自下而上中，我们从树的底部字母开始打印到顶部的字母。因此，输出将是:

Output: r, t, a, b, t, a, a, o, c, n, o

trie的自下而上的遍历类似于树的后序遍历。
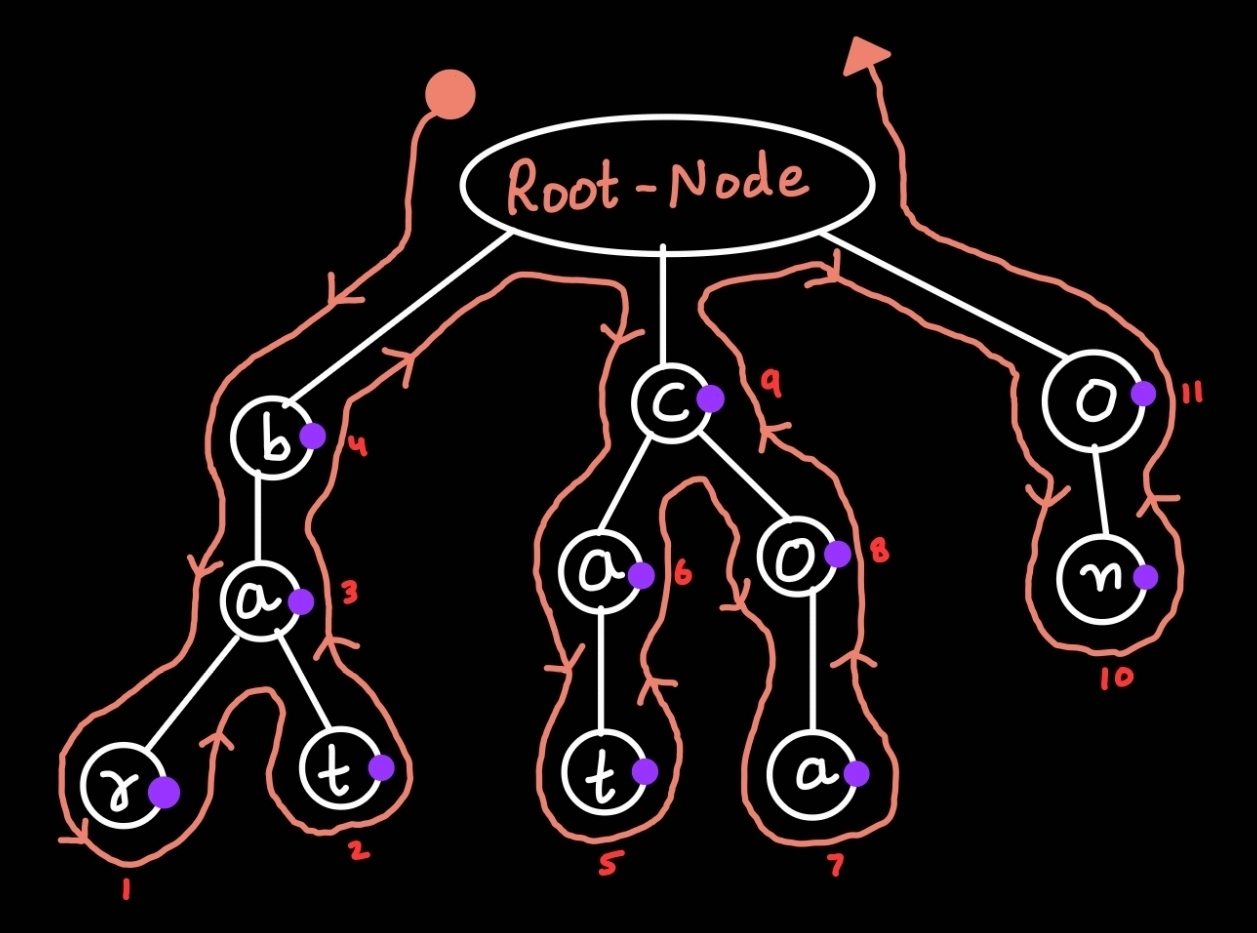
Trie3
这棵树的后序输出是。{ r, t, a, b, t, a, a, o, c, n, o }

算法

开始B-print。

我们以递归方式从上到下移动。
如果（头是NULL），则返回。
如果（头是NOT-NULL），则递归移动到下一个节点（子节点）。
我们一直往下走，直到找不到包含 "我们=1 "值的节点，因为其中的字母表将是这个词的最后一个字母表。
当我们返回时打印节点的值/字母表。

结束B-print。

代码

#include <bits/stdc++.h>

using namespace std;

/*------------Structure of trie-node-------------*/
struct T_node {
  bool we;
  T_node *child[26];        
  T_node()     //To create new node
  {
    we = false;
    for (int i = 0; i < 26; ++i) {
      child[i] = NULL;    //Initializing all child value to null
    }
  }
};


class trie {
  public:
    T_node *root;
  trie()        //Constructor
  {
    root = new T_node();
  }
  
  void insert(string );    //Fuction to insert
  
  void b_print(T_node *);     //Function to print in Bottom-up manner
  
};
  
/*-------------Function to insert the string--------------*/
  void trie::insert(string data) {
    T_node *head = root;        //assigning root to head
    int length = data.size();   //length of word
    int in= 0;      //"in" is for index for child[]
    int h = 0;      //'h' is for height or level of tree
    while (h < length) {
      in = data[h] - 'a';
      if (head->child[in] == NULL) {
        head->child[in] = new T_node();
      }
      head = head->child[in];
      h++;
    }
    if (head != NULL) {
    //assign the "we" true which represent the end of word
      head->we = true;    
    }
  }
  
/*-----------B-print Function to print data--------------*/
  void trie::b_print(T_node *head) {
    if (head == NULL)
        return;
        
      int i = 0;
      while (i <= 25) {
        if (head->child[i] != NULL && head->we != true) {
          b_print(head->child[i]);      //Recursive call
          cout <<"  "<< (char)(i + 97);     //To print alphabet
        }
        i++;
      }
  }


/*--------------Driver Function--------------*/
int main() {
  trie t1;    //"t1" is the Object of trie
  
  /*
       Root-Node
    /      |      \
   b       c       o
   |      / \      |
   a     a   o     n
  / \    |   |
 r   t   t   a
  
  */
  
  t1.insert("cat");
  t1.insert("coa");
  t1.insert("bar");
  t1.insert("bat");
  t1.insert("on");
  t1.b_print(t1.root);
  
  return 0;
}

Output:  r  t  a  b  t  a  a  o  c  n  o

复杂度

时间效率取决于 trie 数据结构，并且取决于用户输入的关键词字符串。
时间复杂性。O(K)，其中'K'是给定词的总长度（大约）。因为，程序将通过 trie 中的每一个节点来打印，例如: 如果给定的词是 {cat, rat, hat, set}
"cat "的长度=3
"rat
"的长度=3 "
hat "的长度
=3
"set "的长度=3
那么K = (3 + 3 + 3 + 3)
K = 12
空间复杂性：O(K)，其中 "K "代表三角形中的字母数量。因为程序会去打印三角形中的每一个节点。