如何在JavaScript中实现堆排序

简介

在本指南中，我们将探讨堆排序--它背后的理论以及如何在JavaScript中实现堆排序。

我们将从它所基于的数据结构开始（这里有一个巨大的预示：它是一个堆！），如何对该数据结构进行操作，以及该数据结构如何被用作高效排序算法的手段。

数据结构和排序算法是编程中的核心概念。一个计算机程序一直在处理大型数据集，不厌其烦地检索和注入数据。我们组织这些数据集并对其进行操作的方式是非常重要的，因为它直接影响到用户与我们的应用程序进行互动的便利性和速度。

一个排序算法的评估基于两个特征：算法使用的时间和空间是数据集大小的一个函数。它们分别被称为时间复杂度和空间复杂度，并允许我们在平均和最佳情况下对算法进行 "对比"。

堆排序被认为是一种高效的算法，其平均时间复杂度为θ*（n log(n*)）。

尽管存在其他算法在平均情况下优于堆排序，但它的重要性取决于它在最坏情况下与最佳情况下具有相同的功效，使其在不同的数据集上具有稳定的运行时间，而一些算法可能会受到或大或小的影响--这取决于其基础机制。

JavaScript中的堆排序

堆排序是一种就地的、非稳定的、基于比较的排序算法。

它不需要辅助数据结构--它对数据进行就地排序并影响原始数据**（就地**）。它不保留相对顺序或相等的元素。如果你在未排序的集合中有两个值相同的元素，它们的相对顺序可能会在排序后的集合中改变（或保持不变）（非稳定）。最后，元素之间进行比较以找到它们的顺序**（基于比较**）。

尽管Heap Sort是就地的（不需要辅助数据结构），但为了使实现更清晰一些，我们将在排序过程中招募一个额外的数组。

堆排序的基础机制相当简单，有些人甚至称它为**"改进的选择排序"**。

它首先将未排序的数组转换为一个堆--最大堆或最小堆。在最大堆的情况下，每个父级元素持有的值都比它的子级元素大，使得根元素成为堆中最大的元素，反之亦然。

堆排序依赖于这个堆的条件。

在每次迭代中，算法都会移除堆的根元素并将其推入一个空数组。每次移除后，堆都会自我恢复，将其第二大（或第二小）的元素冒到根上，以保持其堆条件。这个过程也被称为堆化（heapifying），你会经常看到人们把这样做的方法称为堆排序（heapify）。

堆排序继续将新定位的根元素移入排序后的数组中，直到没有剩余的元素。

以这种方式使用最大堆将导致数组中的元素以降序排列。如果要使数组按升序排列，就必须选择最小堆。

这种自我排序和选择性删除的方式让人想起了选择排序（除去自我排序的部分），因此人们将其并列。

什么是堆？

堆是一种树状的数据结构。我们将使用的堆的类型是二叉树（一种类似于树枝的数据结构，必然从一个节点开始，如果要分支，最多允许有两个从每个节点延伸出来的继承者）。虽然存在少数类型的堆，但堆有两个明显的特征。

1. 堆必须是*完整的，*这意味着树的每一层都应该从左到右被填满，而且不允许在没有填满上一层所有可能的节点的情况下创建树的另一层。

2. 每个节点必须持有一个大于或等于（在最小堆的情况下，小于或等于）其每一个后代的值。这被称为 "堆条件"。

将堆映射到数组

到目前为止，我们所定义和描述的堆只是一个图，一个圆和线的集合。为了在基于JavaScript的计算机程序中使用这种结构，我们需要把它重新加工成一个数组或一个列表。

幸运的是，这是一个相当直接的操作，模仿了我们最初建立堆的方式。我们将元素从堆中读出并移到数组中，其顺序与我们将它们放入堆中的顺序相同：从左到右，逐级进行。

一个堆和其数组对应的例子，在这种转移之后。

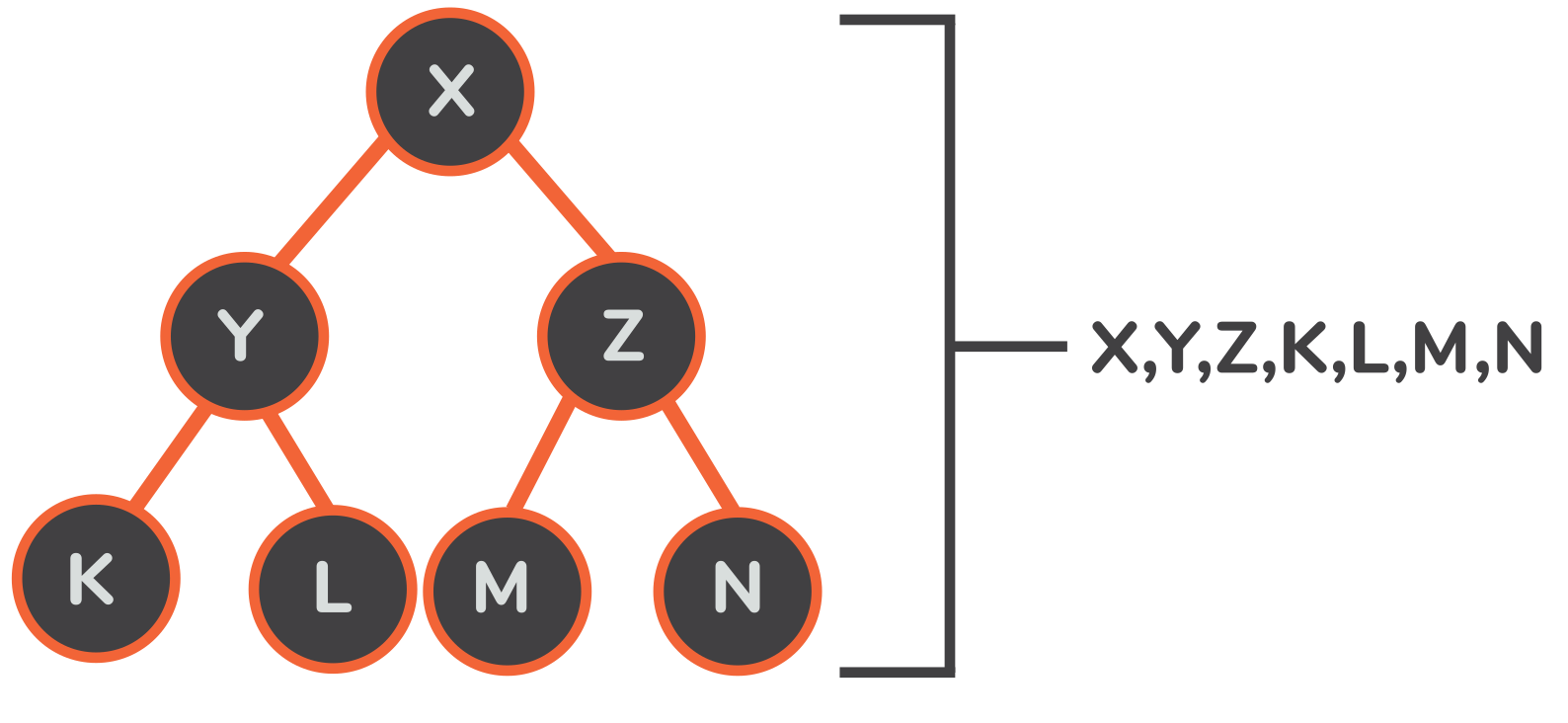
这样一来，我们不仅可以用代码来表达堆，而且还获得了一个指南针，可以在堆内进行导航。 我们可以推导出三个方程，给定每个节点的索引，就可以指出它的父节点和它在数组中的左右子节点的位置。

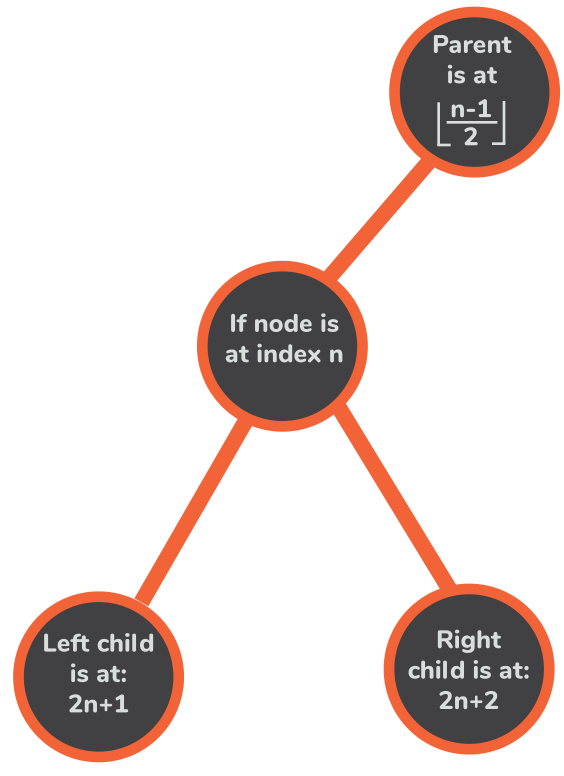
在JavaScript中创建一个堆

现在已经有了堆的详细定义，我们可以继续把它作为一个JavaScript类来实现。

在本指南中，我们将创建并使用一个最大堆。由于最大堆和最小堆之间的区别是微不足道的，并不影响堆排序算法背后的一般逻辑，因此，最小堆的实现以及通过堆排序创建升序是一个改变比较运算符的问题。

让我们继续下去，定义一个MaxHeap 类。

class MaxHeap{
    constructor(){
        this.heap = [];
    }

    parentIndex(index){
        return Math.floor((index-1)/2);
    }

    leftChildIndex(index){
        return (2*index + 1);
    }

    rightChildIndex(index){
        return (2*index + 2);
    }
}

在MaxHeap 类中，我们已经定义了一个初始化空数组的构造函数。以后，我们将创建额外的函数来填充这个数组内的堆。

然而，就目前而言，我们只创建了一些辅助函数，这些函数将返回给定节点的父节点和子节点的索引。

向堆中插入元素

每当一个新的元素被插入到堆中，它就会被放在底层的最右边的节点旁边（数组表示中的最后一个空位），或者，如果底层已经满了，就放在新层的最左边的节点上。在这种情况下，堆的第一个要求：树的完整性，得到了保证。

再往前走，可能已经被干扰的堆的属性需要重新建立。为了将新元素移到堆上的适当位置，需要将其与父元素进行比较，如果新元素比其父元素大，则两个元素要进行交换。

新元素在堆中不断上升，同时在每一级与它的父元素进行比较，直到最后恢复堆的属性。

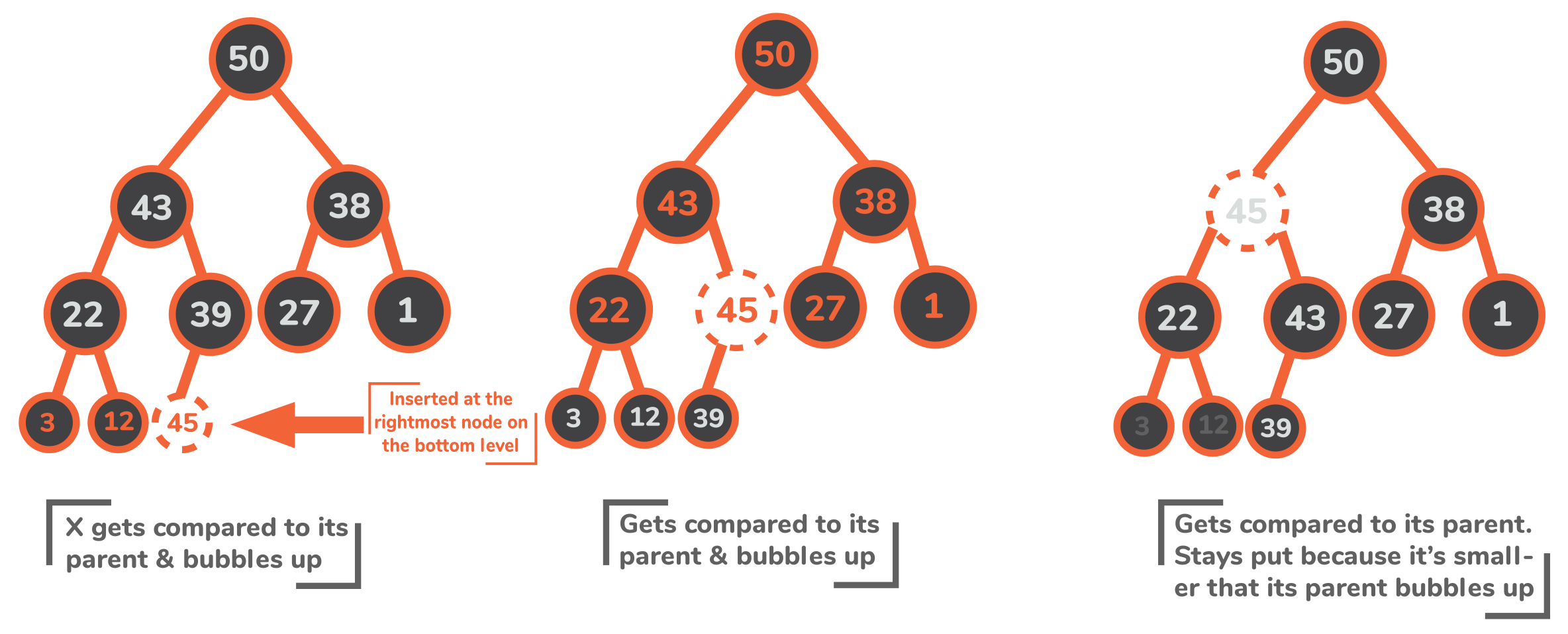
让我们把这个功能添加到我们之前创建的MaxHeap类中。

 swap(a, b) {
        let temp = this.heap[a];
        this.heap[a] = this.heap[b];
        this.heap[b] = temp;
    }

 insert(item) {
    this.heap.push(item);
    var index = this.heap.length - 1;
    var parent = this.parentIndex(index);
    while(this.heap[parent] && this.heap[parent] < this.heap[index]) {
        this.swap(parent, index);
        index = this.parentIndex(index);
        parent = this.parentIndex(index);
    }
}

swap() 作为一个辅助方法加入，以节省代码中的冗余，因为在插入新元素时，我们可能要执行几次这个动作--一个介于0和log(n)之间的数字（在新元素大于堆根的情况下，我们必须让它爬上整个树，其高度为log(the-total-number-of-its-elements)--换句话说，是很多。

insert() 操作如下。

1. 使用内置的JavaScript方法将给定的元素附加到heap ：push() 。
2. 将heap 的最后一个元素标记为index ，将其父元素标记为parent 。
3. 当堆中存在一个索引为parent (this.heap[parent])的元素，而这个元素恰好比index (this.heap[parent] < this.heap[index)的元素小，insert() 方法继续将两者交换 (this.swap(parent, index))，并将其光标向上移动一级。

从堆中删除元素

一个堆只允许删除根元素，之后我们就会得到一个完全扭曲的堆。因此，我们首先要通过将堆的最后一个节点移到根上来恢复完整的二叉树属性。然后我们需要将这个错位的值泡下去，直到堆的属性恢复原状。

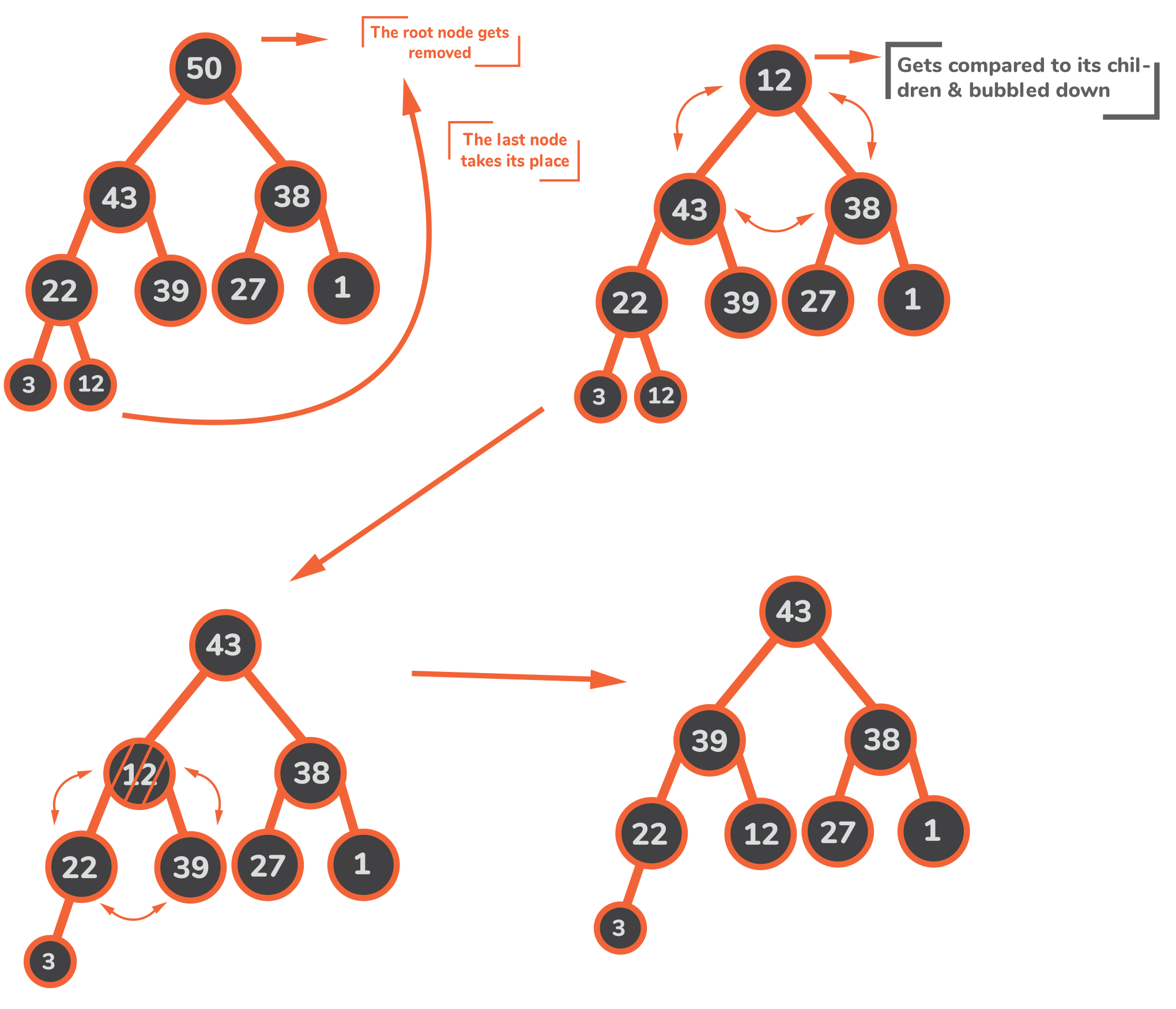
delete() {
    var item = this.heap.shift();
    this.heap.unshift(this.heap.pop());
    var index = 0;
    var leftChild = this.leftChildIndex(index);
    var rightChild = this.rightChildIndex(index);
    while(this.heap[leftChild] && this.heap[leftChild] > this.heap[index] || this.heap[rightChild] > this.heap[index]){
        var max = leftChild;
        if(this.heap[rightChild] && this.heap[rightChild] > this.heap[max]){
            max = rightChild
        }
        this.swap(max, index);
        index = max;
        leftChild = this.leftChildIndex(max);
        rightChild = this.rightChildIndex(max);
    }
    return item;
}

我们在MaxHeap 类内创建的delete() 方法，其操作方式如下。

1. 该方法从收获最大的元素开始--因此是堆的数组表示中的第一个元素。内置的shift() 方法删除数组的第一个元素并返回被删除的元素，然后我们将其存储在item 变量中。
2. heap 的最后一个元素通过pop() 被移除，并通过unshift() 被放置到heap 最近清空的第一个空间。unshift() 是一个内置的 JavaScript 方法，作为shift() 的对应方法。而shift() 移除数组的第一个元素并将其余的元素向后移动一个空间，unshift() 将一个元素推到数组的开头，并将其余的元素向前移动一个空间。
3. 为了能够将新的根向下冒泡，指向它的位置的指针（最初为0）和它的两个子节点（index,rightChild,leftChild ）被创建。
4. while() 循环检查index 节点是否存在一个左边的子节点，以确保下面的另一个层次的存在（还没有检查右边的子节点），如果这个层次的任何子节点比[index]的节点大。
5. 如果满足while循环里面的条件，就会创建一个max 变量来声明左边的节点是该方法目前遇到的最大值。然后在循环内部，在一个if 子句中，我们检查是否存在一个右边的子节点，如果存在，它是否比我们第一次检查的左边子节点大。如果右边的孩子的值确实更大，那么它的索引将取代max 中的值。
6. 通过this.swap(max, index) ，持有较大数值的子代与它的父代进行交换。
7. 该方法在while循环结束时将其假想的光标向下移动了一级，并继续重复执行while循环中的代码，直到其条件不再成立。

在JavaScript中实现堆排序

最后，为了实现本指南所承诺的目标，我们创建了一个heapSort() 函数（这次是在MaxHeap 类之外），并向它提供了一个我们想要排序的数组。

function heapSort(arr){
    var sorted = [];
    var heap1 = new MaxHeap();
    
    for(let i=0; i<arr.length; i++){
        heap1.insert(arr[i]);
    }
    
    for(let i=0; i<arr.length; i++){
        sorted.push(heap1.delete());
    }
    return sorted;
}

heapSort()把要排序的数组作为它的参数。然后，它创建一个空数组来放置排序后的版本，以及一个空堆，通过它来执行排序。

然后，heap1 填充了arr 的元素，并逐一删除，将删除的元素推入排序后的数组。heap1 在每次删除时都会自我组织，所以只要把其中的元素推到排序数组中就可以得到一个排序的数组了。

让我们创建一个数组，测试一下这个问题。

let arr = [1, 6, 2, 3, 7, 3, 4, 6, 9];
arr = heapSort(arr);

console.log(arr);

结论

在本指南中，我们已经了解了堆数据结构和堆排序的操作方法。

虽然不是最快的算法，但当数据被部分排序或需要一个稳定的算法时，堆排序是有优势的。

尽管我们使用了一个额外的数据结构来实现它，但堆排序本质上是一种原地排序算法，因此，在内存使用有问题的时候也可以使用。