Vue3 双端对比的diff算法
双端对比 diff 算法
顾名思义,双端对比,左端和右端。通过左端和右端的收缩比较,可以精准的确定旧节点和新节点的改变范围。
左侧对比
先来一张图给大家看看,咱们先别看右侧的流程图(那是关于往右侧新增节点的流程)
解析:
c1:旧的子节点的数组,比如:有 A、B 两个元素
c2:新的子节点的数组,比如:有 A、B、C、D 四个元素
i:头部指针,初始为 0,将会向右移动
e1:旧节点数组的指针,指针指向数组末尾,初始化值为c1.length - 1
e2:新节点数组的指针,指针指向数组末尾,初始化值为c2.length - 1
要想知道有哪些节点是需要被新增的,那不得遍历两个数组进行比较嘛,相同就证明不需要新增,不相同就证明旧节点数组没有,新节点数组有的元素,这要新增元素了。这就引出一个索引值i,通过索引值可以得出要新增哪些节点以及新增节点的范围。比如上图中,e1 < i <= e2这个范围就是需要新增节点的范围。i 在什么条件下会移动呢?当然是c1[i]和c2[i]有值的时候啊,所以当i<=e1 && i<=e2,要判断c1[i]和c2[i]是否是相同的 vnode,如果相同就i++,下一轮循环的时候根据这个已自增的 i 取得 vnode。有进行下一轮的比较。
而这个比较方法isSameVNodeType()的实现就是根据 vnode 的 type 属性和 key 属性进行比较。
// n1是旧的vnode n2是新的vnode 返回boolean
function isSameVNodeType(n1: any, n2: any) {
return n1.type === n2.type && n1.key === n2.key
}
所以为什么 vue3 里面渲染列表的时候 v-for 后面要顺便定义 key,就是为了能精准确定两个 vnode 节点是不是相同的 vnode,从而提升渲染时的性能。
如果发现两个 vnode 节点是相同的节点,那么调用 patch 方法,否则直接跳出循环,拿到这个i值,这个 i 值就是要新增节点的开始索引值。
while (i <= e1 && i <= e2) {
const n1 = c1[i] // 旧的vnode节点
const n2 = c2[i] // 新的vnode节点
if (isSameVNodeType(n1, n2)) {
patch(n1, n2, container, parentComponent, anchor)
} else {
break
}
i++
}
右侧对比
和左侧对比的方向相反,注意的是:右侧对比不再以 i 为索引获取 vnode 节点,而是用 e1 和 e2 作为索引获取 vnode,并且不再对 i 自增,反而利用 e1 和 e2 自减来获取不同的 vnode 节点。但是判断条件还是一样的i <= e1 && i <= e2,i 始终为 0。
while (i <= e1 && i <= e2) {
const n1 = c1[e1]
const n2 = c2[e2]
if (isSameVNodeType(n1, n2)) {
patch(n1, n2, container, parentComponent, anchor)
} else {
break
}
e1--
e2--
}
新增节点
新增节点我们使用Node.insertBefore(),第一个入参用于插入的节点,第二个入参用于指定插在哪个节点之前,如果入参为 null,将会插入的节点插入到末尾。
我们可以利用第二个入参为 null 来实现右侧添加节点。至于往左侧添加节点我们可以在第二个参数填上对应的引用节点就好。
图1中循环下来 i、e1、e2 的值分别是:
i: 2
e1: 1
e2: 3
图2中循环下来 i、e1、e2 的值分别是:
i: 0
e1: -1
e2: 1
可以看出:i 始终大于 e1,始终小于等于 e2
if (i > e1) {
if (i <= e2) {
const nextPos = e2 + 1
// c2[nextPos].el 将会拿到 Node实例 ,c2[nextPos]是vnode对象
const anchor = nextPos < c2.length ? c2[nextPos].el : null
while (i <= e2) {
// 新增
patch(null, c2[i], container, parentComponent, anchor)
i++
}
}
}
// 核心的新增节点函数
export function insert(child: any, container: any, anchor: any = null) {
container.insertBefore(child, anchor)
}
anchor 是作为一个锚点的存在,当右侧添加节点的时候,它将会是 null,会传入 insertBefore 的第二个参数。当需要左边添加节点的时候,他将作为被插入节点的下一个节点。这里可能很难理解,我打个比方:
图2中需要我们插入 C 和 D 到 A 之前,那么这个 anchor 锚点就是 A。前面两个 while 循环(分别是左侧对比和右侧对比)走完之后,i 还是 0,e1 是-1,e2 是 1。最后nextPos = 2,nextPos < c2.length这个判断自然就走 true 了,而c2[nextPos].el就是 A。
在下一段代码 patch 的时候,内部调用 insertBefore 就能把 D、C 插入到 A 之前,仔细你会发现其实是先插入 D 再插入 C 的 🤣。
😟why?为什么是先插入 D 再插入 C 呢?
因为 i 为 0,c2[i]取得是 c2 的第一个元素(D)进行 patch,patch 完之后 i 自增加一,这时候才开始取第二个元素(C)进行 patch。
while (i <= e2) {
// 新增
patch(null, c2[i], container, parentComponent, anchor)
i++
}
删除节点
i: 2
e1: 3
e2: 1
右侧删除节点时:i、e1、e2 的值分别是:
i: 0
e1: 1
e2: -1
可以知道规律:c1 的数组长度大于 c2 的数组长度的时候,需要删除节点。删除的范围将会是:i > e2的时候
if (i > e2) {
while (i <= e1) {
remove(c1[i].el)
i++
}
}
// 删除节点的核心函数
// 这里可以换成 child.remove()
export function remove(child: HTMLElement) {
const parent = child.parentNode
if (parent) {
parent.removeChild(child)
}
}
右侧删除节点,删除的顺序是:C、D
左侧删除节点,删除的顺序是:A、B
进入真正复杂的 diff 场景
diff 有几个场景:
- 删除场景:旧节点的子节点中间部分中某一个节点在新节点的子节点中不存在。旧节点需要删除该子节点。
- 新增场景:新节点的子节点中间部分中某一个节点在旧节点的子节点中不存在。旧节点需要新增该子节点。
- 更新场景:旧节点的子节点某一个节点在新节点的子节点中状态发生改变了。旧节点需要更新该子节点。
- 移动场景:旧节点的子节点某一个节点在新节点的子节点中位置发生改变了。旧节点需要移动该子节点到目标位置。
先考虑删除和更新的逻辑(交换位置和新增节点逻辑先不考虑)
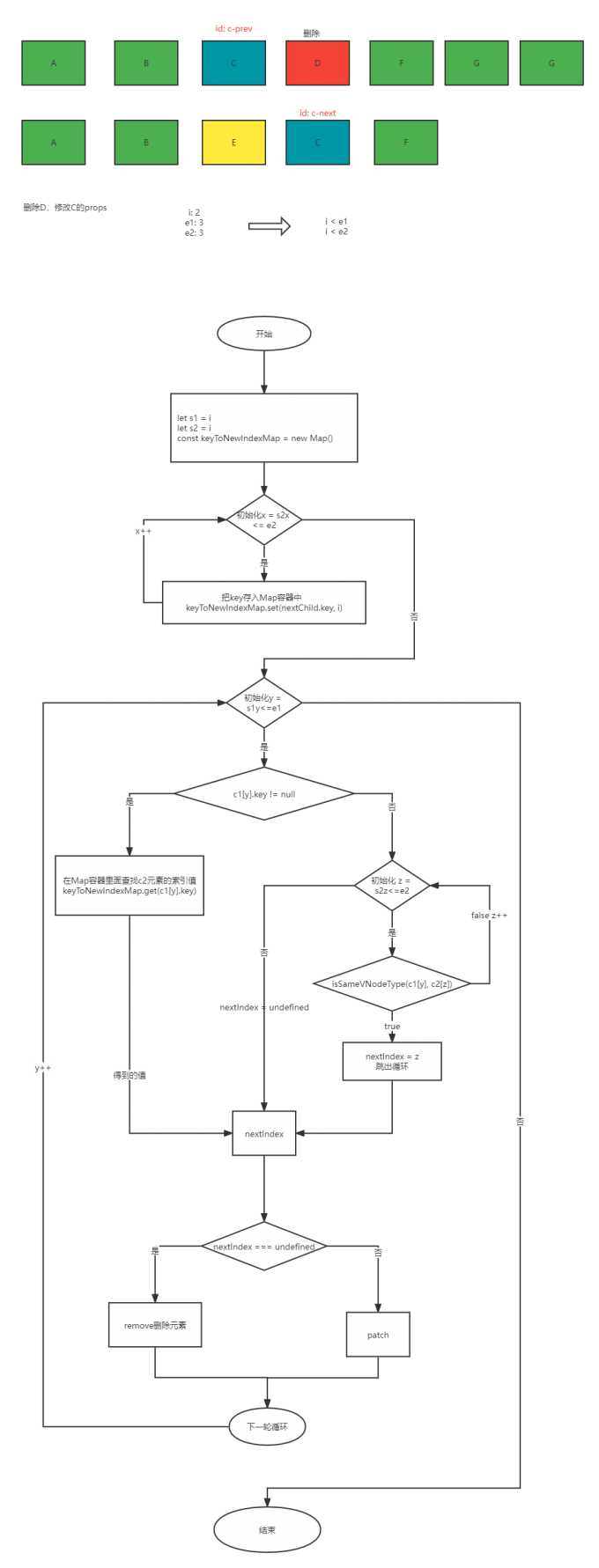
这里给一个例子:
我们把之前的左端对比和右端对比结合起来,计算出 i、e1、e2 的值就能知道中间部分的范围在哪了。
上图所示:中间部分的范围:i ~ e1、i ~ e2
目光聚焦到 c1 和 c2 的中间部分,都有 C,但是 C 的 property 并不相同,主要还是 id 不一样,需要 patch。再看 D,D 在 c2 数组里面是没有的,所以 D 需要被删除。
那怎么知道 c1 的元素在 c2 有没有呢?那就需要双重遍历了,先遍历 c1 的中间部分,拿到 c1 的索引值再遍历 c2 的中间部分,拿着这个 c1 的元素依次跟 c2 的元素进行比较,第一轮比较完之后接着拿 c1 的下一个元素跟 c2 的元素进行比较。不过这样做的话时间复杂度是 O(n^2)。要想快速找到 c1 的元素对应再 c2 上有没有,我们可以用映射查找的方式(Map)。
先把 c2 的中间部分的每一个元素的索引值都存入一个 Map 中。当遍历 c1 的时候,首先去 Map 查找看看有没有对应的元素。如果有值,直接走 patch,如果没有值,才用上面所说的双重遍历的方式查找,还是没有查找到在 c2 对应的元素呢?说明该元素是需要被删除的。当然如果查找到了还是走 patch。这样时间复杂度就从 O(n^2)变成 O(1)了。这也是为什么列表渲染的时候我们必须给元素添加一个唯一值 key 提升渲染性能
// 处理中间部分
// a b (c d) e f
// a b (e c) e f
let s1 = i
let s2 = i
// 为了能使用映射查找方式需要的map容器,提高patch的效率
const keyToNewIndexMap = new Map()
// 遍历c2中间部分
for (let i = s2; i <= e2; i++) {
const nextChild = c2[i]
keyToNewIndexMap.set(nextChild.key, i)
}
// 遍历c1中间部分,找出c1在c2对应的元素,如果找不到,就删除,找到了就更新走patch
// 遍历旧节点
for (let i = s1; i <= e1; i++) {
const prevChild = c1[i]
let nextIndex
if (prevChild.key != null) {
nextIndex = keyToNewIndexMap.get(prevChild.key)
} else {
for (let j = s2; j <= e2; j++) {
if (isSameVNodeType(prevChild, c2[j])) {
nextIndex = j
break
}
}
}
if (nextIndex === undefined) {
hostRemove(prevChild.el)
} else {
patch(prevChild, c2[nextIndex], container, parentComponent, null)
}
}
Map 实际上用 vnode.key 作为键去存储 c2 元素的索引值,这个 vnode.key 就是上面代码中的nextChild.key和prevChild.key,这也是为什么列表渲染的时候我们必须给元素添加一个唯一值 key 提升渲染性能。
删除逻辑的优化点:
上面的代码就是删除节点和更新节点的逻辑了,其中也有一个可以优化的点,那就是当知道 c2 中的元素都已经被比较过了以后,c1 中剩余的元素就没必要处理了,直接删除,提高了性能。
如图,红色部分为新增代码。
我们需要定义两个变量:
toBePatched:表示需要patch的元素的数量
patched:表示已经patch的元素的数量
已经执行了 patch 处理的时候,我们可以把 patched 自增加一,当patched >= toBePatched时,也就是说该 patch 的都已经 patch 完了,那剩下 c1 的元素干嘛管他呢,都认定为 c2 中没有的元素,代表要删除的元素,直接 remove 掉就好了。之后的流程不必往下走了直接进入下一轮循环。
let s1 = i
let s2 = i
// 新增
let toBePatched = e2 - s2 + 1
let patched = 0
const keyToNewIndexMap = new Map()
// 遍历c2中间部分
for (let i = s2; i <= e2; i++) {
const nextChild = c2[i]
keyToNewIndexMap.set(nextChild.key, i)
}
for (let i = s1; i <= e1; i++) {
const prevChild = c1[i]
let newIndex
// 如果该patch的都已经patch完了,之后的元素直接remove掉
if (patched >= toBePatched) {
hostRemove(prevChild.el)
continue
}
if (prevChild.key != null) {
newIndex = keyToNewIndexMap.get(prevChild.key)
} else {
for (let j = s2; j <= e2; j++) {
if (isSameVNodeType(prevChild, c2[j])) {
newIndex = j
break
}
}
}
if (newIndex === undefined) {
hostRemove(prevChild.el)
} else {
patch(prevChild, c2[newIndex], container, parentComponent, null)
// 被patched的数量 +1
patched++
}
}
移动节点逻辑
上图是 diff 算法中需要处理的节点的位置变更场景,通常我们说的 diff 的节点移动逻辑。
图中 E 被移动到了 C、D 的前面,而 C、D 也跟着发生位置的变换,如果我们思考移动逻辑该怎么实现的话,我们会很自然的想到,遍历 c2,让 c2 的每一个元素和 c1 的元素进行比较,看看位置是否发生变化,发生变化就移动到新位置。但是!这种移动逻辑真的太消耗性能了,找这样的逻辑,就需要移动三遍,执行三次insertBefore。
我们不妨换一种逻辑。
首先我们可以给 c1 的中间部分的节点添加一个索引(关于怎么确定中间部分就是通过 i,e1,e2 这些指针来确定 i 的变化范围)
以下是旧节点的索引(为什么是从 2 开始?因为前面还有 A、B,A 是 0,B 是 1)
索引 2 3 4
C D E
映射到已交换位置的新节点上那就是
索引 4 2 3
E C D
仔细观察,C、D 它们之间的关系并没有发生改变,C、D 排列顺序不变,只是 E 被移动到了 C、D 的前面,E 无论插入到哪个位置,比如插入到 C、D 的前面,还是说插入到 C、D 的中间,都不会改变 C、D 的顺序,那我们可以把 C、D 当成一个稳定序列,只需要对 E 执行一次insertBefore就好了啊。这是不是就减少了我们移动元素的个数了呢,从而优化了 diff 的性能。
那怎么确定我们要移动的是 E 呢?而不是 C 或者 D 呢?换言之,哪些是需要被移动的,哪些是不需要移动的?
首先我们需要在中间部分生成这个稳定序列,判断中间部分的每个节点在不在这个稳定序列里面,如果不在,那就意味着这个节点是需要移动的,并且这个稳定序列我想要尽可能长,这样的话就能找到更多需要移动的节点和不需要移动的节点,让优化性能最大化。
尽可能长的稳定序列,稳定递增的子序列,也就是最长递增子序列
关于怎么实现最长递增子序列,这里略过,具体代码在下方。该实现来自 vue3 源码里面的renderer.ts文件。该方法传入的是一个数组,比如[4,2,3],计算出来最长递增子序列是[2,3],返回的是一个索引数组[1,2]。其中 1 2 代表元素在传入的数组中的索引值。
// 最长递增子序列
function getSequence(arr: number[]): number[] {
const p = arr.slice()
const result = [0]
let i, j, u, v, c
const len = arr.length
for (i = 0; i < len; i++) {
const arrI = arr[i]
if (arrI !== 0) {
j = result[result.length - 1]
if (arr[j] < arrI) {
p[i] = j
result.push(i)
continue
}
u = 0
v = result.length - 1
while (u < v) {
c = (u + v) >> 1
if (arr[result[c]] < arrI) {
u = c + 1
} else {
v = c
}
}
if (arrI < arr[result[u]]) {
if (u > 0) {
p[i] = result[u - 1]
}
result[u] = i
}
}
}
u = result.length
v = result[u - 1]
while (u-- > 0) {
result[u] = v
v = p[v]
}
return result
}
拿到这个索引值数组之后,我们就可以拿 c2 的中间部分组成的索引数组和这个索引数组作比较了。
例如:
E C D
[0,1,2] c2的中间部分索引值数组
[1,2] 利用最长递增子序列求出的索引值数组
发现 0 并不在索引值数组中,证明 E 是需要被移动的。
我们稍微在删除节点的逻辑代码上改动:
let s1 = i
let s2 = i
let toBePatched = e2 - s2 + 1
let patched = 0
// 为了能使用映射查找方式需要的map容器,提高patch的效率
const keyToNewIndexMap = new Map()
// 定义数组映射,用于查找出需要移动的元素以及移动的位置在哪(这极大的减少了使用insert api的次数)
const newIndexToOldIndexMap = new Array(toBePatched) // 定长的数组比不定长的数组性能更好
for (let i = 0; i < toBePatched; i++) {
newIndexToOldIndexMap[i] = 0 // 初始化为0,表示没有被移动
}
// 遍历c2中间部分
for (let i = s2; i <= e2; i++) {
const nextChild = c2[i]
keyToNewIndexMap.set(nextChild.key, i)
}
for (let i = s1; i <= e1; i++) {
const prevChild = c1[i]
let newIndex
// 这里是针对删除做优化,c2的中间部分都已经被遍历过了,c1剩下的部分就没必要处理了,直接删除就好。
if (patched >= toBePatched) {
hostRemove(prevChild.el)
continue
}
if (prevChild.key != null) {
newIndex = keyToNewIndexMap.get(prevChild.key)
} else {
for (let j = s2; j <= e2; j++) {
if (isSameVNodeType(prevChild, c2[j])) {
newIndex = j
break
}
}
}
if (newIndex === undefined) {
hostRemove(prevChild.el)
} else {
// 能确认新的节点是存在的
newIndexToOldIndexMap[newIndex - s2] = i + 1 // 这里为什么要+1,因为为0另外代表着该元素在c1上没有,需要新增(涉及到下一小节的新增逻辑)
patch(prevChild, c2[newIndex], container, parentComponent, null)
patched++
}
}
// 根据映射表生成最长递增子序列
const increasingNewIndexSequence = getSequence(newIndexToOldIndexMap)
let j = 0 // 指针
for (let i = 0; i < toBePatched; i++) {
if (i !== increasingNewIndexSequence[j]) {
console.log('需要移动');
}else{
// 不需要移动 指针j++,判断递增子序列的下一个索引是否与 i 相等
j++
}
}
找到需要移动的节点后,我们考虑怎么把他插入到正确的位置了。
insertBefore这个 dom api 是一个插入节点的很好的选择。不过第二个参数锚点的选择需要注意,怎么找好这个锚点?
根据上面的例子,肉眼可见很快就确定了锚点是 C 节点。但是代码层面上怎么实现?我们习惯思维是正序遍历 c2 的中间部分,找 E 的下一个节点作为锚点,在上面例子上或许行得通。但是有没有想过,如果其他情况下,C 也是需要移动位置的节点呢?正序遍历寻找下一个节点,下一个节点未必是一个稳定不变的节点哦。这也得益于 insertBefore 的特性,只能选择下一个节点作为锚点,那如果选择上一个节点作为锚点那就不一样了喔,使用正序遍历就行。
A B [E C D] F G
使用倒叙遍历可以解决这个问题。
- 先在 D 节点开始,因为 F 是固定不变的节点,可以使用 F 作为锚点。
- D 节点被 patched 上去后,D 就变成固定不变的节点了,便可以使用 D 作为锚点。
- 插入 E 的时候,C 已经变成固定不变的节点,可以使用 C 作为锚点。
// 为什么需要倒序遍历呢?因为需要一个固定的节点作为锚点,正序遍历只能确定一个不稳定的锚点
// looping backwards so that we can use last patched node as anchor
let j = increasingNewIndexSequence.length - 1 // 指针
for (let i = toBePatched - 1; i >= 0 ; i--) {
const nextIndex = i + s2
const nextChild = c2[nextIndex]
const anchor = nextIndex + 1 < l2 ? c2[nextIndex + 1].el : null // 防止nextIndex + 1超出 l2 范围
if (i !== increasingNewIndexSequence[j]) {
console.log('需要移动')
hostInsert(nextChild.el, container, anchor)
} else {
// 不需要移动 指针j++,判断递增子序列的下一个索引是否与 i 相等
j--
}
}
新增节点逻辑
上一小节留了一个小坑,打算在这补一下。
newIndexToOldIndexMap创建索引值映射表的时候,都初始化为0,然而在patch的时候我偏偏让元素+1,就是为了有一个值能区分该节点需不需要被新建。
没有需要新增的节点
[4,2,3] ==加1后==> [5,3,4]
有需要新增的节点
[0,4,2,3] ==加1后==> [0,5,3,4]
那么只需要判断newIndexToOldIndexMap[i]是否等于0即可判断出是否需要执行patch()
let j = increasingNewIndexSequence.length - 1 // 指针
for (let i = toBePatched - 1; i >= 0 ; i--) {
const nextIndex = i + s2
const nextChild = c2[nextIndex]
const anchor = nextIndex + 1 < l2 ? c2[nextIndex + 1].el : null
// 新增节点
if(newIndexToOldIndexMap[i] === 0){
patch(null, nextChild, container, parentComponent,anchor)
continue
}
if (j < 0 || i !== increasingNewIndexSequence[j]) {
console.log('需要移动')
hostInsert(nextChild.el, container, anchor)
} else {
j--
}
}
使用 moved 标识符优化性能
提高diff的性能对vue的渲染速度来说非常重要,而毫无意义的计算最长递增子序列明显拖慢了diff的速度。
这时候我们可以用moved这个布尔值变量去表示c1对比c2来说,c2里面有没有节点被移动,用来判断是否需要执行最长递增子序列的计算。
moved ? getSequence() : []
那应该如何判断c2里面节点需不需要移动了呢?
我们需要定义一个变量maxNewIndexSoFar用来记录上一个节点在映射表keyToNewIndexMap里的值
// newIndex也是keyToNewIndexMap映射表的映射值哦
if (newIndex >= maxNewIndexSoFar){
maxNewIndexSoFar = newIndex
}else{
moved = true
}
如果新的映射值比上一个映射值大,那么赋值作为上一个映射值,否则判定为已经移动了。
最后生成最长递增子序列的时候加以判断
const increasingNewIndexSequence = moved ? getSequence(newIndexToOldIndexMap) : []
这样就避免了没有意义的计算,提高了性能。
结尾
vue3的双端对比diff算法的比vue2的简单粗暴的diff算法性能上更高效,但是实现起来也会更绕,那么下一篇文章我们来聊聊组件的更新逻辑。