【考研代码笔记】数据结构

【数据结构学习笔记】4.1串的定义、基本操作、存储结构

1.串的定义

• 串，即字符串(String)是由零个或多个字符组成的有限序列。

• 子串：串中任意个连续的字符组成的子序列。

• 主串：包含子串的串。

• 字串在主串中的位置：字符在串中的序号。

• 子串在主串中的位置：子串的第一个字符在主串中的位置。

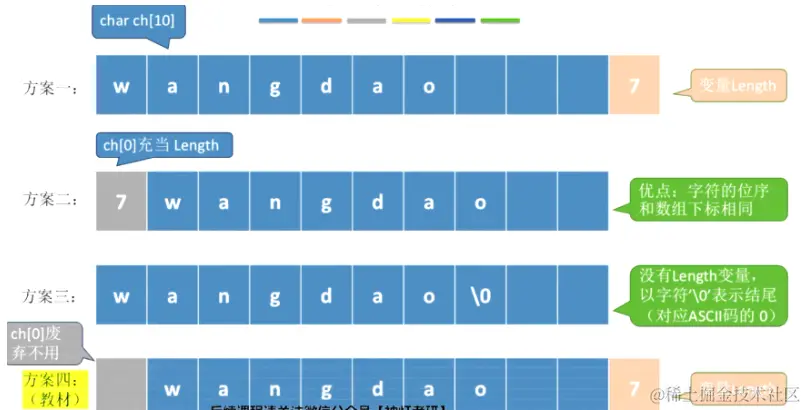
2.串的顺序存储

#define MAXLEN 255      //预定义最大串长为255
//静态数组实现(定长顺序存储) --->系统自动回收存储空间 
typedef struct{
    char ch[MAXLEN];    //每个分量存储一个字符
    int length;         //串的实际长度 
}SString; 
​
//动态数组实现(堆分配存储)--->需要手动free内存 
typedef struct{
    char *ch;       //按串长分配存储区，ch指向串的基地址
    int length;     //串的长度 
}HString;
HString S;
S.ch=(char *)malloc(MAXLEN * sizeof(char));
S.length=0;

3.串的链式存储

typedef struct StringNode{
    char ch;        //每个结点存1个字符
    struct StringNode * next; 
}StringNode,* String;

• 一个字符内存为1B，一个指针的内存为4B，导致存储密度低

typedef struct StringNode{
    char ch[4];     //每个结点存1个字符
    struct StringNode * next; 
}StringNode,* String;

• 每个结点多存一些字符，来提高存储密度。

4.基本操作的实现

• SubString(&Sub,S,pos,len):求子串。用Sub返回串S 的第pos个字符起长度为len的子串。

  #define MAXLEN 255      //预定义最大串长为255
  typedef struct{
      char ch[MAXLEN];    //每个分量存储一个字符
      int length;         //串的实际长度 
  }SString; 
  ​
      //子串范围越界
      if(pos+len-1>S.length)
          return false;
      for(int i=pos;i<pos+len;i++)
          Sub.ch[i-pos+1]=S.ch[i];
      Sub.length=len;
      return true; 
  }
  

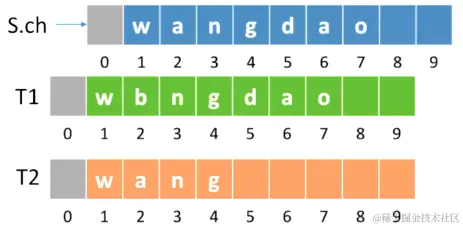
• StrCompare(S,T):比较操作。若S>T，则返回值>0；若S=T，则返回值=0；若S<T，则返回值<0

  int StrCompare(SString S,SString T){
      for(int i=1;i<S.length&&i<T.length;i++){
          if(S.ch[i]!=T.ch[i])
              return S.ch[i]-T.ch[i];
      }
      //扫描过的所有字符都相同，则长度长的串更大
      return S.length-T.length; 
  }
  

• Index(S,T):定位操作。若主串S中存在与串T值相同的子串，则返回它在主串S中第一次出现的位置；否则函数值为0。

  int Index(SString S,SString T){
      int i=1,n=StrLength(S),m=StrLength(T);
      SString sub;        //用于暂存子串
      while(i<=n-m+1){
          SubString(sub,S,i,m);
          if(StrCompare(sub,T)!=0)    ++i;
          else return i;  //返回子串在主串中的位置 
      } 
      return 0;   //S中不存在与T相等的子串 
  }
  

  一段段向后遍历。