概率论复习路线本文已参与「新人创作礼」活动，一起开启掘金创作之路。前言 MindMap 概率论部分数理统计部分概率

本文已参与「新人创作礼」活动，一起开启掘金创作之路。

前言

希望能够通过一份简单的路线，实现精准高效的备战明天的考试。话不多说，冲冲冲！

内容分为概率论与数理统计两个部分，中间的串联是第五章的大数定律和中心极限定理。

MindMap

概率论部分

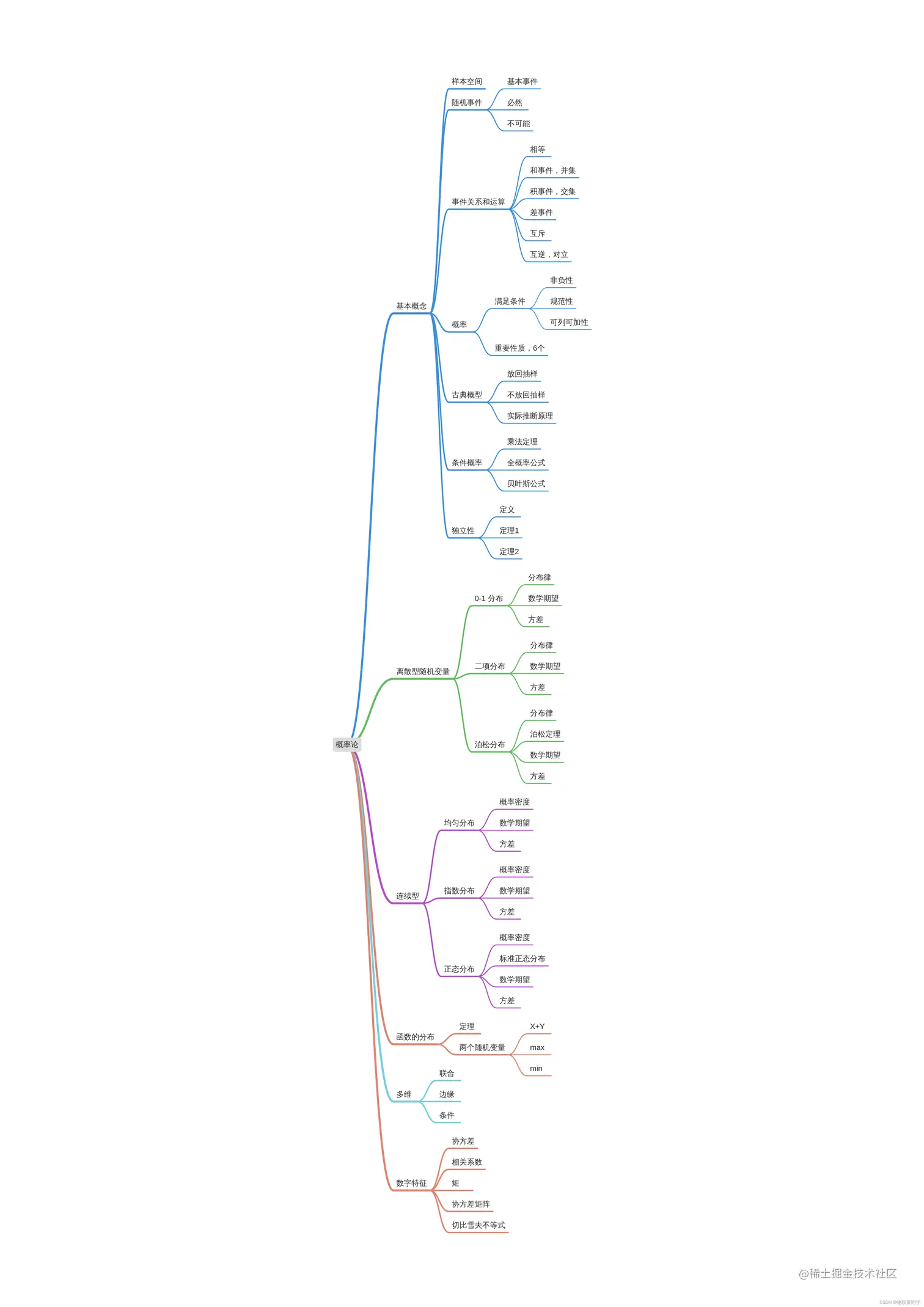
在这里插入图片描述

数理统计部分

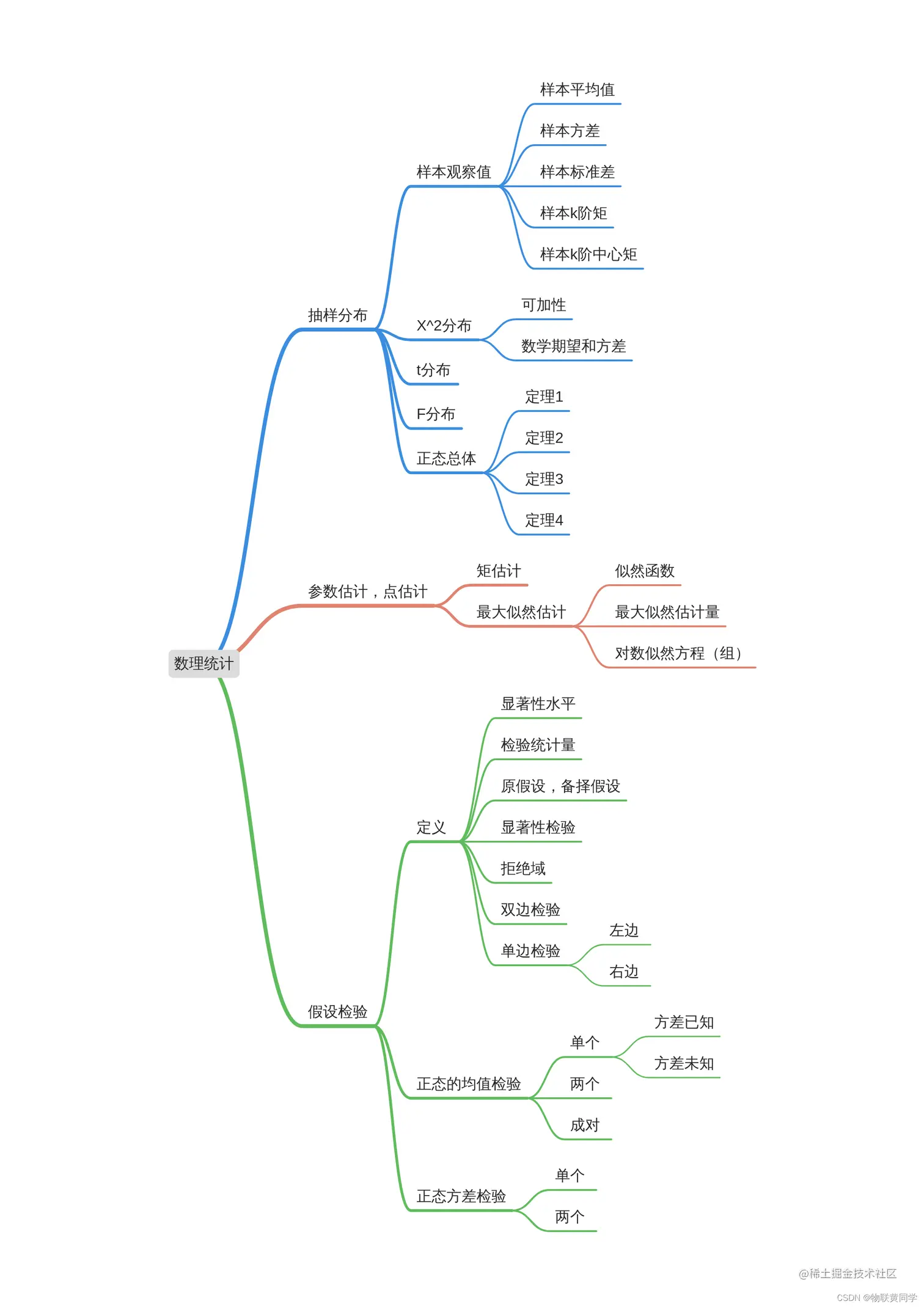
在这里插入图片描述

概率论

基本概念

这个部分的内容，我的建议是直接看我之前的blog，或者看书以及其他网课ppt之类的。

关于随机变量的分布函数我不去列举，大家可以直接通过分布律或者概率密度推导

离散型

0-1 分布

X~b(p)

分布律

P\{X=k \} = p^k(1-p)^{1-k}, \qquad k = 1, 0

X	0	1
p_k	1-p	p

数学期望

E(X) = p

方差

D(X) = (1-p)\cdot p

二项分布

X~b(n, p)

分布律

P\{X=k \} = p^k(1-p)^{1-k}

数学期望

E(X) = np

方差

D(X) = n(1-p)\cdot p

泊松分布

X~π(λ)

分布律

P\{X=k \} = \frac{\lambda^ke^{-\lambda}}{k!}, \qquad k=0,1,2...

泊松定理

就是用泊松去逼近二项，np=λ

\lim_{n\rightarrow \infty}{C_n^k(1-p_n)^{n-k}} = \frac{\lambda^ke^{-\lambda}}{k!}

数学期望

E(X) = \lambda

方差

D(X) = \lambda

连续型

均匀分布

X~U(a, b)

概率密度

f(x) = \left \{ \begin{aligned} &\frac{1}{b-a}, &\qquad a < x < b \\ &0, &\qquad 其他 \end{aligned} \right.

期望

E(X) = \frac {a+b}{2}

方差

D(X) = \frac{(b-a)^2}{12}

指数分布

X~E(θ)

概率密度

f(x) = \left \{ \begin{aligned} &\frac{1}{\theta}{e^{-x/\theta}}, &\qquad a < x < b \\ &0, &\qquad 其他 \end{aligned} \right.

期望

E(X) = \theta

方差

D(X) = \theta^2

正态分布

X~N(μ, σ)

概率密度

f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-u)^2}{2\sigma^2}}, \qquad -\infty < x < \infty

标准正态分布

X\sim N(0, 1^2)\\ \varphi(x) = \frac{1}{\sqrt{2\pi}}e^{-x^2/2}

期望和方差，一般情况下只要先化成标准正态分布，然后用标准的正态分布的方差和期望求解即可。

期望

E(x) = \mu

方差

D(X) = \sigma^2

概率论部分的除了这些其实还有像随机变量函数，多维的边缘和条件以及联合，还有第四章的协方差和矩。但是这些内容我就不提了，有需要的可以看blog或者课本。

数理统计

开摆了，这个直接看吧。我要回去睡觉了。