动态规划常见算法题

不同路径

分析

• 机器人只能向下移动-或者向右移动

设计

• 状态转移方程 dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
• 初始化 dp[0][0] = 1
• return dp[m - 1][n - 1] - 因为索引从0开始

代码

var uniquePaths = function (m, n) {
let dp = new Array(m).fill(0).map(() => new Array(n).fill(0));
for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
    if (i == 0 || j == 0) dp[i][j] = 1;
    else dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
    }
}
return dp[m - 1][n - 1]
}

最小路径和

设计

• 状态转移方程 dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]
• return dp[row - 1][col - 1]

代码

var minPath = function(grid) {
// 行
const row = grid.length;
// 列
const col = grid[0].length;
// 创建dp数组
const dp = Array.from(new Array(row), () => new Array(col).fill(1));
// 到达第一个点的路径和肯定为grid[0][0]值本身
dp[0][0] = grid[0][0];
// 求第一行每个点的最短路径和
for (let i = 1; i < col; i++) {
    dp[0][i] = grid[0][i] + dp[0][i - 1];
}
// 求第一列每一行的最短路径和
for (let j = 1; j < row; j++) {
    dp[j][0] = grid[j][0] + dp[j - 1][0];
}

for (let i = 1; i < row; i++) {
    for (let j = 1; j < col; j++) {
      dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]
    }
}
return dp[row - 1][col - 1];
}

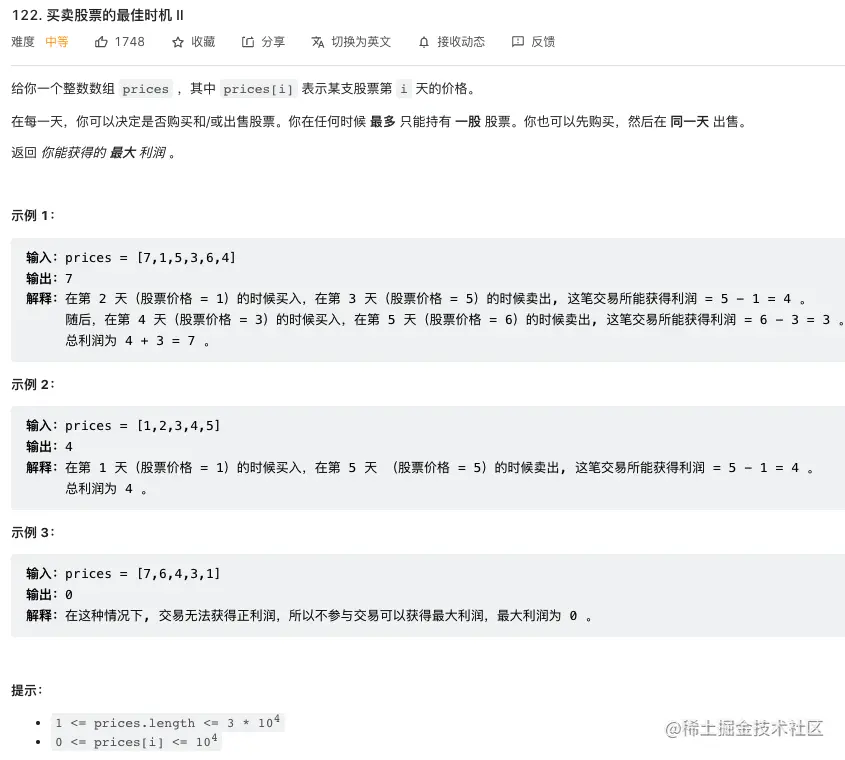
买卖股票的最佳时机 II

设计

• 两种情况买进和卖出
• 最后一天只能卖出买进没有意义
• 设置dp[i][0]卖出-dp[i][1] 买进
• return dp0

代码

var maxProfit = function(prices) {
    const n = prices.length;
    let dp0 = 0, dp1 = -prices[0]
    for (let i = 1; i < n; ++i) {
        let newDp0 = Math.max(dp0, dp1 + prices[i])
        let newDp1 = Math.max(dp1, dp0 - prices[i])
        dp0 = newDp0
        dp1 = newDp1
    }
    return dp0
}