矩阵分解，也叫矩阵因数化，是将一个矩阵分割成多个部分的过程。在数据科学的背景下，你可以用它来选择数据的一部分，目的是在不丢失很多信息的情况下降低维度（例如在主成分分析中，你会在本篇文章的后面看到）。一些操作也更容易在分解后的矩阵上进行计算。

在这篇文章中，你将了解到矩阵的重分解（eigendecomposition）。理解它的一种方法是把它看作是一种特殊的基数变化（关于基数变化的更多细节见我上一篇文章）。你将首先学习特征向量和特征值，然后你将看到它如何被应用于主成分分析（PCA）。其主要思想是将矩阵的特征分解 ，作为基数的改变，其中新的基向量是特征向量。

特征向量和特征值

正如你在《数据科学基本数学》第7章中所看到的，你可以将矩阵视为线性变换。这意味着，如果你把任何一个向量 ，并把矩阵 ，你会得到一个变换后的向量 。

以以下例子为例。

和

如果你把 应用于向量 （用矩阵-向量积），你会得到一个新的向量。

让我们来画出初始向量和转换后的向量。

u = np.array([1.5, 1])

A = np.array([
   [1.2, 0.9],
   [0, -0.4]
])

v = A @ u

plt.quiver(0, 0, u[0], u[1], color="#2EBCE7", angles='xy', scale_units='xy', scale=1)

plt.quiver(0, 0, v[0], v[1], color="#00E64E", angles='xy', scale_units='xy', scale=1)

# [...] Add axes, styles, vector names

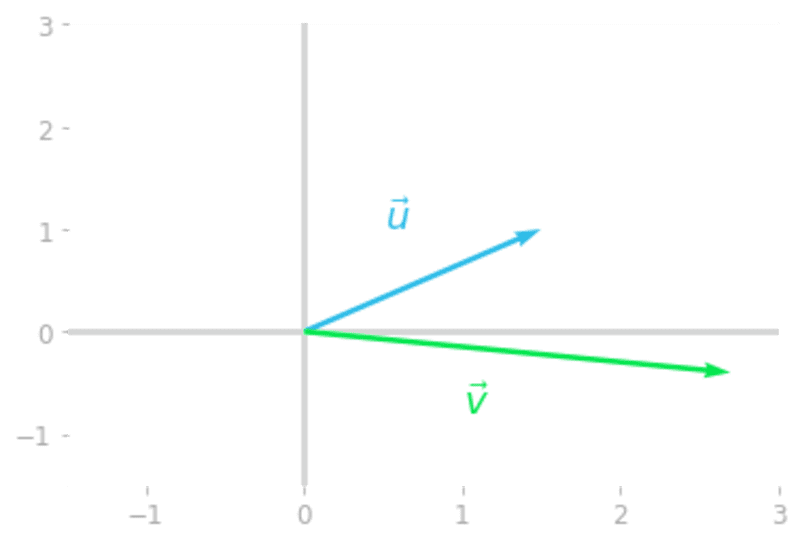
图 1: 矩阵 将向量 转变为向量.

注意，如你所料，转换后的向量 与初始向量 的方向不同。这种方向的改变是大多数你可以通过 来转换的向量的特征。

然而，以下面这个向量为例。

让我们把矩阵 应用于向量 ，得到一个向量 。

x = np.array([-0.4902, 0.8715])

y = A @ x

plt.quiver(0, 0, x[0], x[1], color="#2EBCE7", angles='xy',
          scale_units='xy', scale=1)

plt.quiver(0, 0, y[0], y[1], color="#00E64E", angles='xy',
          scale_units='xy', scale=1)

# [...] Add axes, styles, vector names

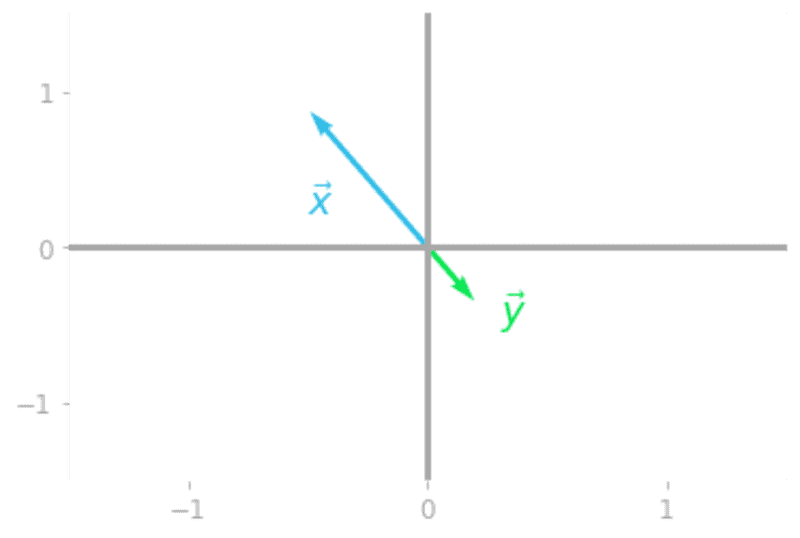
图2：特殊向量 被矩阵 转变。

你可以在图2中看到，向量 与矩阵 有一个特殊的关系：它被重新缩放（有一个负值），但初始向量 和转换后的向量 都在同一直线上。

向量 是 的一个特征向量。它只被一个值缩放，这个值被称为矩阵 的一个特征值。矩阵 的特征向量是一个在被矩阵转换时被收缩或拉长的向量。特征值是该向量被收缩或拉长的比例系数。

在数学上，如果矢量 是 的一个特征向量。

（读作 "lambda"）是对应于特征向量 的特征值。

特征向量

矩阵的特征向量是非零向量，只有当矩阵应用于它们时才会被重新缩放。如果缩放系数是正的，初始向量和转换后的向量的方向是一样的，如果是负的，它们的方向就会颠倒。

特征向量的数量

一个-by- 矩阵最多有 个线性独立的特征向量。然而，每个特征向量乘以一个非零标量也是一个特征向量。如果你有。

那么。

与 任何非零值。

这就排除了作为特征向量的零向量，因为你会有

在这种情况下，每个标量都将是一个特征值，因此将是未定义的。

实践项目。主成分分析

主成分分析，或称PCA，是一种你可以用来降低数据集维度的算法。例如，它对于减少计算时间、压缩数据或避免所谓的 "维度诅咒"很有用。它对于可视化的目的也很有用：高维数据很难可视化，减少维度的数量来绘制你的数据可能是有用的。

在这个实践项目中，你将使用在《数据科学基本数学》一书中学习到的各种概念，如基数变化（第7.5节和第9.2节，这里有一些例子），eigendecomposition（第9章）或协方差矩阵（第2.1.3节）来了解PCA是如何工作的。

在第一部分中，你将了解投影、解释方差和误差最小化之间的关系，首先是一些理论，然后通过对啤酒数据集（啤酒消费量与温度的关系）进行编码来了解PCA。请注意，你还会在《数据科学基本数学》中找到另一个例子，你将使用Sklearn在音频数据上使用PCA，根据音频样本的类别进行可视化，然后对这些音频样本进行压缩。

架构之下

理论背景

PCA的目标是将数据投射到一个较低维度的空间，同时尽可能多地保留数据中的信息。这个问题可以看作是一个垂直最小二乘法问题，也叫正交回归。

在这里你会看到，当投影线对应于数据方差最大的方向时，正交投影的误差是最小的。

方差和投射

首先要理解的是，当你的数据集的特征不是完全不相关的时候，一些方向会比其他方向有更大的方差。

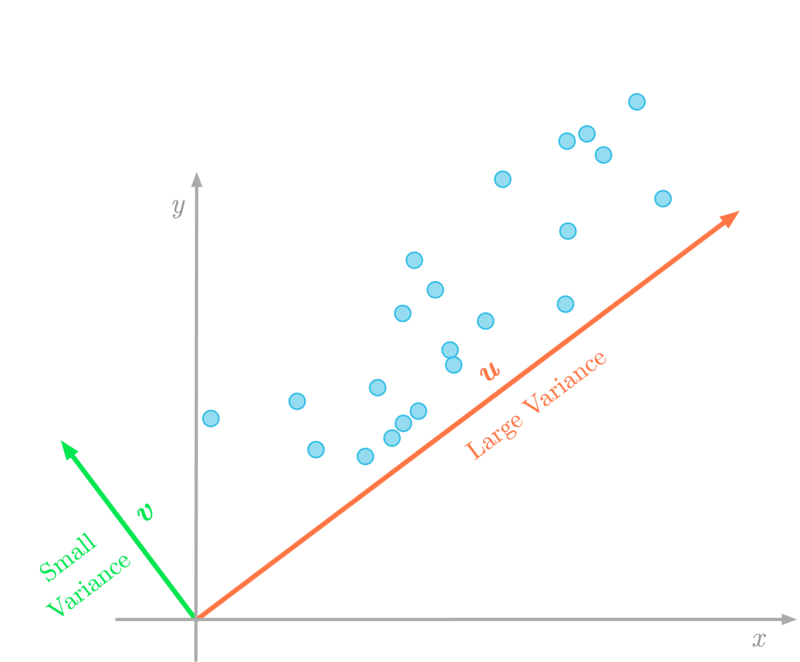
图3：数据在向量 （红色）方向的方差大于向量 （绿色）方向。

将数据投射到一个较低维度的空间意味着你可能会失去一些信息。在图3中，如果你把二维数据投射到一条线上，投射数据的方差会告诉你失去多少信息。例如，如果投影数据的方差接近零，这意味着数据点将被投影到非常接近的位置：你会失去很多信息。

出于这个原因，PCA的目标是改变数据矩阵的基础，使具有最大方差的方向（图3中的 ）成为第一个主成分。第二个成分是具有最大方差的方向，它与第一个成分正交，以此类推。

当你找到PCA的分量后，你改变了数据的基础，使这些分量成为新的基础向量。这个转换后的数据集有新的特征，这些特征是分量，是初始特征的线性组合。减少维度是通过只选择一些成分来完成的。

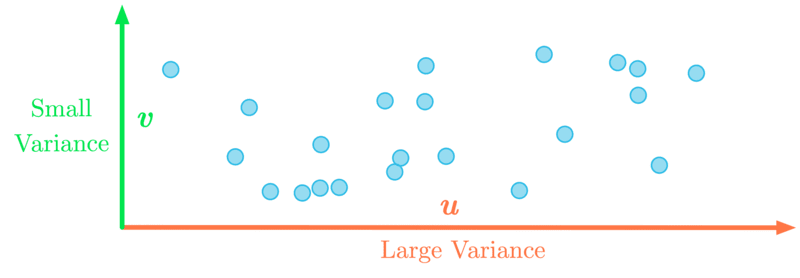
图4：改变基础，使最大方差在-轴上。

作为说明，图4显示了改变基础后的数据：最大方差现在与-轴相关。例如，你可以只保留这个第一维。

换句话说，用改变基础来表达PCA，它的目标是找到一个新的基础（它是初始基础的线性组合），其中数据的方差沿着第一个维度达到最大。

误差最小化

找到方差最大化的方向类似于最小化数据和其投影之间的误差。

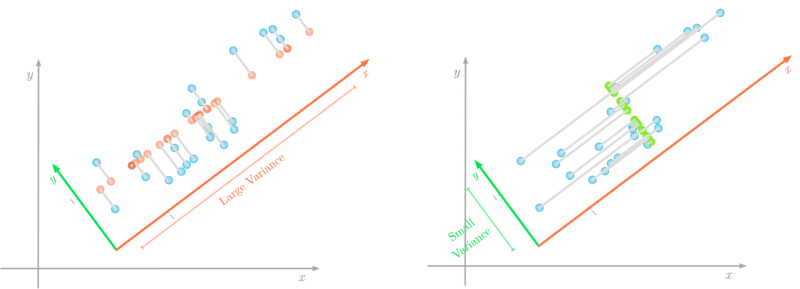
图5：方差最大的方向也是与最小的误差相关的方向（用灰色表示）。

你可以在图5中看到，较低的误差显示在左图中。由于投影是正交的，与你投影的线的方向相关的方差不会影响误差。

寻找最佳方向

在改变了数据集的基础之后，你应该有一个接近零的特征之间的协方差（例如，如图4）。换句话说，你希望转换后的数据集有一个对角线协方差矩阵：每一对主成分之间的协方差都等于零。

你可以在《数据科学基本数学》第9章中看到，你可以使用eigendecomposition将一个矩阵对角化（使矩阵成为对角线）。因此，你可以计算出数据集协方差矩阵的特征向量。它们将为你提供新的基础的方向，其中协方差矩阵是对角线的。

总而言之，主成分是作为数据集协方差矩阵的特征向量来计算的。此外，特征值给你相应特征向量的解释方差。因此，通过按照特征值的递减顺序对特征向量进行排序，你可以按照重要性顺序对主成分进行排序，并最终删除与小方差相关的成分。

计算PCA

数据集

让我们用显示2015年巴西圣保罗的啤酒消费和温度的啤酒数据集来说明PCA是如何工作的。

让我们加载数据并绘制消费量与温度的函数关系。

data_beer = pd.read_csv("https://raw.githubusercontent.com/hadrienj/essential_math_for_data_science/master/data/beer_dataset.csv")
plt.scatter(data_beer['Temperatura Maxima (C)'],
           data_beer['Consumo de cerveja (litros)'],
           alpha=0.3)

# [...] Add labels and custom axes

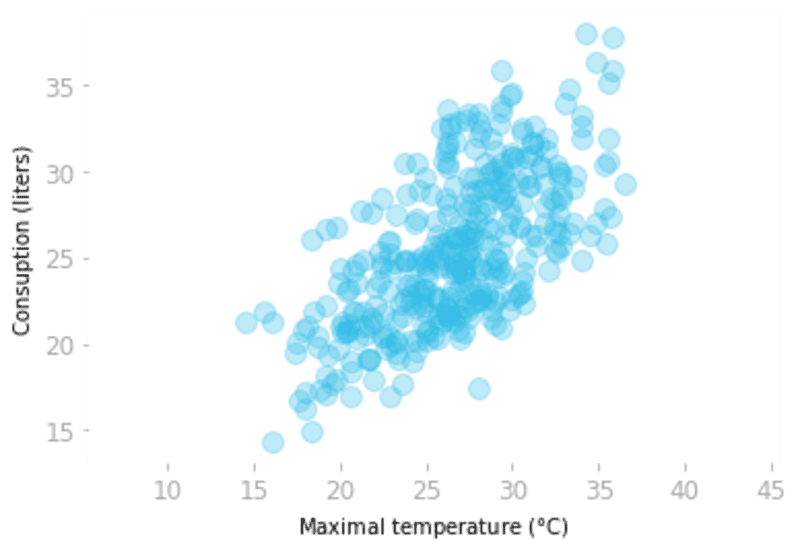
图6：啤酒的消费量与温度的关系。

现在，让我们用两个变量：温度和消费量创建数据矩阵 。

X = np.array([data_beer['Temperatura Maxima (C)'],
           data_beer['Consumo de cerveja (litros)']]).T

X.shape

(365, 2)

矩阵 有365行和两列（两个变量）。

协方差矩阵的Eigendecomposition

正如你所看到的，第一步是计算数据集的协方差矩阵。

C = np.cov(X, rowvar=False)

C

array([[18.63964745, 12.20609082],
       [12.20609082, 19.35245652]])

记住，你可以这样理解：对角线的数值分别是第一个和第二个变量的方差。两个变量之间的协方差约为12.2。

现在，你将计算这个协方差矩阵的特征向量和特征值。

eigvals, eigvecs = np.linalg.eig(C)
eigvals, eigvecs

(array([ 6.78475896, 31.20734501]),
array([[-0.71735154, -0.69671139],
       [ 0.69671139, -0.71735154]]))

你可以将特征向量存储为两个向量 和 。

u = eigvecs[:, 0].reshape(-1, 1)

v = eigvecs[:, 1].reshape(-1, 1)

让我们用数据绘制特征向量（注意，你应该使用居中的数据，因为它是用来计算协方差矩阵的数据）。

你可以通过其相应的特征值来缩放特征向量，这就是解释方差。出于可视化的目的，让我们使用三个标准差的向量长度（等于解释方差的平方根的三倍）。

X_centered = X - X.mean(axis=0)

plt.quiver(0, 0,
          2 * np.sqrt(eigvals[0]) * u[0], 2 * np.sqrt(eigvals[0]) * u[1],
          color="#919191", angles='xy', scale_units='xy', scale=1,
          zorder=2, width=0.011)

plt.quiver(0, 0,
          2 * np.sqrt(eigvals[1]) * v[0], 2 * np.sqrt(eigvals[1]) * v[1],
          color="#FF8177", angles='xy', scale_units='xy', scale=1,
          zorder=2, width=0.011)

plt.scatter(X_centered[:, 0], X_centered[:, 1], alpha=0.3)

# [...] Add axes

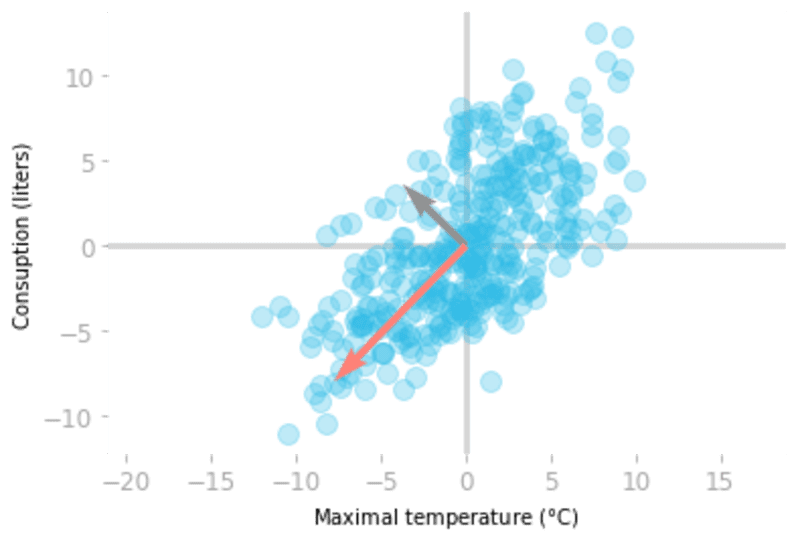
图7：特征向量 （灰色）和 （红色）根据解释的方差进行缩放。

你可以在图7中看到，协方差矩阵的特征向量给你提供了数据的重要方向。红色的向量 ，与最大的特征值有关，因此对应于具有最大方差的方向。灰色的向量 是与 正交的，是第二主成分。

然后，你只需要用特征向量作为新的基向量来改变数据的基础。但首先，你可以将特征向量按照特征值的递减顺序进行排序。

sort_index = eigvals.argsort()[::-1]
eigvals_sorted = eigvals[sort_index]

eigvecs_sorted = eigvecs[:, sort_index]

eigvecs_sorted

array([[-0.69671139, -0.71735154],
       [-0.71735154,  0.69671139]])

现在你的特征向量已经排序了，让我们来改变数据的基础。

X_transformed = X_centered @ eigvecs_sorted

你可以绘制转换后的数据，以检查主成分现在是否不相关。

plt.scatter(X_transformed[:, 0], X_transformed[:, 1], alpha=0.3)

# [...] Add axes

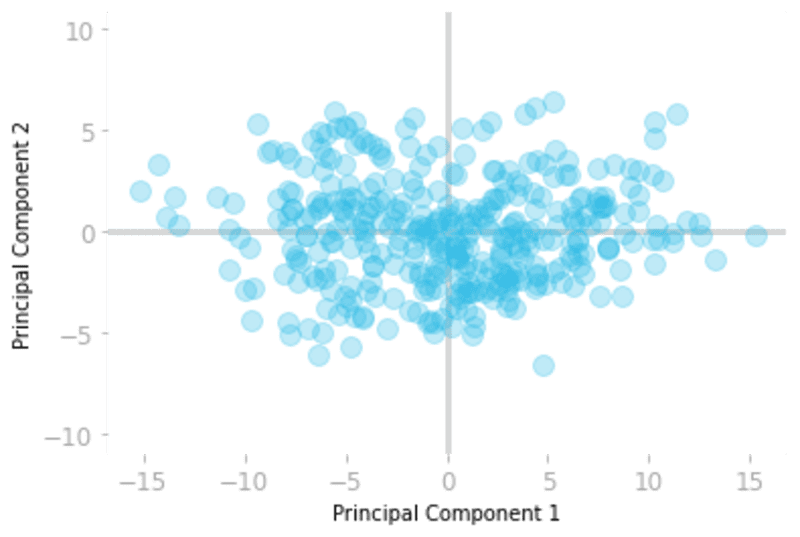
图8：在新基础上的数据集。

图8显示了新基础下的数据样本。你可以看到，第一个维度（-轴）对应于具有最大方差的方向。

你可以在这个新的基础上只保留数据的第一个分量，而不会损失太多的信息。

协方差矩阵还是奇异值分解？

使用协方差矩阵来计算PCA的一个注意事项是，当有许多特征时，它可能很难计算（如音频数据，如本实践的第二部分）。出于这个原因，人们通常倾向于使用单值分解（SVD）来计算PCA。