了解Keras中的简单递归神经网络

今天你吸猫了么
51 阅读7分钟

本教程是为那些希望了解递归神经网络（RNN）如何工作以及如何通过Keras深度学习库使用它们的人设计的。虽然解决问题和构建应用程序所需的所有方法都是由Keras库提供的，但深入了解一切工作原理也很重要。在这篇文章中，将逐步展示RNN模型中发生的计算。接下来，我们将开发一个完整的用于时间序列预测的端到端系统。

在完成本教程后，您将知道。

  • RNN的结构
  • 当给定一个输入时，RNN是如何计算输出的
  • 如何为Keras中的SimpleRNN准备数据
  • 如何训练一个SimpleRNN模型

让我们开始吧。

Umstead state park

了解Keras中的简单递归神经网络

教程概述

本教程分为两部分，它们是。

  1. RNN的结构
    1. 与RNN的不同层相关的不同权重和偏置。
    2. 当给定一个输入时，如何进行计算以计算输出。
  2. 一个完整的时间序列预测的应用。

前提条件

在你开始实施RNN之前，假定你对RNN有一个基本的了解。递归神经网络和支持它们的数学简介》给了你一个关于RNN的快速概述。

现在让我们直接进入实施部分。

导入部分

为了开始实施RNN，让我们添加导入部分。

from pandas import read_csv
import numpy as np
from keras.models import Sequential
from keras.layers import Dense, SimpleRNN
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
import math
import matplotlib.pyplot as plt

Keras SimpleRNN

下面的函数返回一个模型，其中包括一个SimpleRNN 层和一个Dense 层，用于学习顺序数据。input_shape 指定了参数(time_steps x features) 。我们将简化一切，使用单变量数据，即只使用一个特征；下面将讨论时间_步骤。

def create_RNN(hidden_units, dense_units, input_shape, activation):
    model = Sequential()
    model.add(SimpleRNN(hidden_units, input_shape=input_shape, 
                        activation=activation[0]))
    model.add(Dense(units=dense_units, activation=activation[1]))
    model.compile(loss='mean_squared_error', optimizer='adam')
    return model

demo_model = create_RNN(2, 1, (3,1), activation=['linear', 'linear'])

返回的对象demo_model ，有2个通过SimpleRNN 层创建的隐藏单元和1个通过Dense 层创建的密集单元。input_shape 被设置为3×1，为了简单起见，两层中都使用了一个linear 激活函数。只需回顾一下，线性激活函数f(x)=xf(x) = x不会使输入发生变化。该网络看起来如下。

如果我们有mm隐藏单元（在上述情况下m=2m=2），那么。

  • 输入：xinRx\\in R
  • 隐蔽单元：hinRmh\\in R^m
  • 输入单元的权重：w_xinRmw\_x\\in R^m
  • 隐藏单元的权重：w_hinRmxmw\_h\\in R^{mxm}
  • 隐藏单元的偏置：b_hinRmb\_h\\in R^m
  • 密集层的权重：w_yinRmw\_y\\in R^m
  • 密集层的偏置：b_y/inRb\_y /in R

让我们来看看上面的权重。注意：由于权重是随机初始化的，这里粘贴的结果会与你的不同。重要的是了解被使用的每个对象的结构是什么样子的，以及它是如何与其他对象相互作用以产生最终输出的。

wx = demo_model.get_weights()[0]
wh = demo_model.get_weights()[1]
bh = demo_model.get_weights()[2]
wy = demo_model.get_weights()[3]
by = demo_model.get_weights()[4]

print('wx = ', wx, ' wh = ', wh, ' bh = ', bh, ' wy =', wy, 'by = ', by)

wx =  [[ 0.18662322 -1.2369459 ]]  wh =  [[ 0.86981213 -0.49338293]
 [ 0.49338293  0.8698122 ]]  bh =  [0. 0.]  wy = [[-0.4635998]
 [ 0.6538409]] by =  [0.]

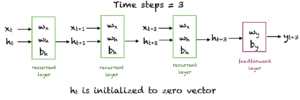
现在让我们做一个简单的实验，看看来自SimpleRNN和Dense层的各层如何产生输出。请看这个图。

Layers Of A Recurrent Neural Network

递归神经网络的层数

我们将在三个时间步骤中输入x ，让网络产生一个输出。隐性单元在时间步骤1、2和3的值将被计算出来。h_0h\_0被初始化为零向量。输出o_3o\_3是由h_3h\_3和w_yw\_y计算出来的。由于我们使用的是线性单元，所以不需要激活函数。

x = np.array([1, 2, 3])
# Reshape the input to the required sample_size x time_steps x features 
x_input = np.reshape(x,(1, 3, 1))
y_pred_model = demo_model.predict(x_input)


m = 2
h0 = np.zeros(m)
h1 = np.dot(x[0], wx) + h0 + bh
h2 = np.dot(x[1], wx) + np.dot(h1,wh) + bh
h3 = np.dot(x[2], wx) + np.dot(h2,wh) + bh
o3 = np.dot(h3, wy) + by

print('h1 = ', h1,'h2 = ', h2,'h3 = ', h3)

print("Prediction from network ", y_pred_model)
print("Prediction from our computation ", o3)

h1 =  [[ 0.18662322 -1.23694587]] h2 =  [[-0.07471441 -3.64187904]] h3 =  [[-1.30195881 -6.84172557]]
Prediction from network  [[-3.8698118]]
Prediction from our computation  [[-3.86981216]]

在太阳黑子数据集上运行RNN

现在我们明白了SimpleRNN和Dense层是如何组成的。让我们在一个简单的时间序列数据集上运行一个完整的RNN。我们需要遵循以下步骤

  1. 从一个给定的URL读取数据集
  2. 将数据分成训练集和测试集
  3. 将输入数据准备成所需的Keras格式
  4. 创建一个RNN模型并训练它
  5. 在训练集和测试集上进行预测，并打印两组数据的均方根误差
  6. 查看结果

第1、2步：读取数据并分成训练和测试两部分

下面的函数从一个给定的URL中读取训练和测试数据，并将其分割成给定比例的训练和测试数据。使用scikit-learn的MinMaxScaler ，在对数据进行0和1之间的缩放后，返回训练和测试数据的单维数组。

# Parameter split_percent defines the ratio of training examples
def get_train_test(url, split_percent=0.8):
    df = read_csv(url, usecols=[1], engine='python')
    data = np.array(df.values.astype('float32'))
    scaler = MinMaxScaler(feature_range=(0, 1))
    data = scaler.fit_transform(data).flatten()
    n = len(data)
    # Point for splitting data into train and test
    split = int(n*split_percent)
    train_data = data[range(split)]
    test_data = data[split:]
    return train_data, test_data, data

sunspots_url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/monthly-sunspots.csv'
train_data, test_data, data = get_train_test(sunspots_url)

第3步：为Keras重塑数据

下一步是为Keras模型训练准备数据。输入数组的形状应该是这样的。total_samples x time_steps x features.

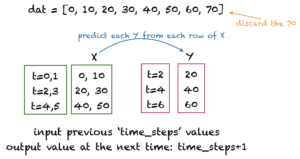
有很多方法来准备用于训练的时间序列数据。我们将用不重叠的时间步骤创建输入行。下图中显示了一个时间步数=2的例子。这里time_steps表示用于预测时间序列数据的下一个值的前一个时间步骤的数量。

How Data Is Prepared For Sunspots Example

如何为太阳黑子准备数据的例子

下面的函数get_XY() 将一个一维数组作为输入，并将其转换为所需的输入X 和目标Y 数组。我们将使用12time_steps 作为太阳黑子的数据集，因为太阳黑子的周期一般为12个月。你可以尝试使用其他数值的time_steps 。

# Prepare the input X and target Y
def get_XY(dat, time_steps):
    # Indices of target array
    Y_ind = np.arange(time_steps, len(dat), time_steps)
    Y = dat[Y_ind]
    # Prepare X
    rows_x = len(Y)
    X = dat[range(time_steps*rows_x)]
    X = np.reshape(X, (rows_x, time_steps, 1))    
    return X, Y

time_steps = 12
trainX, trainY = get_XY(train_data, time_steps)
testX, testY = get_XY(test_data, time_steps)

第4步：创建RNN模型和训练

对于这一步，我们可以重新使用我们上面定义的create_RNN() 函数。

model = create_RNN(hidden_units=3, dense_units=1, input_shape=(time_steps,1), 
                   activation=['tanh', 'tanh'])
model.fit(trainX, trainY, epochs=20, batch_size=1, verbose=2)

第5步：计算并打印均方根误差

函数print_error() ，计算实际值和预测值之间的均方误差。

def print_error(trainY, testY, train_predict, test_predict):    
    # Error of predictions
    train_rmse = math.sqrt(mean_squared_error(trainY, train_predict))
    test_rmse = math.sqrt(mean_squared_error(testY, test_predict))
    # Print RMSE
    print('Train RMSE: %.3f RMSE' % (train_rmse))
    print('Test RMSE: %.3f RMSE' % (test_rmse))    

# make predictions
train_predict = model.predict(trainX)
test_predict = model.predict(testX)
# Mean square error
print_error(trainY, testY, train_predict, test_predict)

Train RMSE: 0.058 RMSE
Test RMSE: 0.077 RMSE

第6步：查看结果

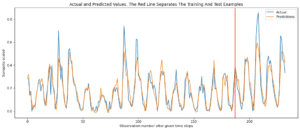
下面的函数绘制了实际目标值和预测值。红线将训练和测试数据点分开。

# Plot the result
def plot_result(trainY, testY, train_predict, test_predict):
    actual = np.append(trainY, testY)
    predictions = np.append(train_predict, test_predict)
    rows = len(actual)
    plt.figure(figsize=(15, 6), dpi=80)
    plt.plot(range(rows), actual)
    plt.plot(range(rows), predictions)
    plt.axvline(x=len(trainY), color='r')
    plt.legend(['Actual', 'Predictions'])
    plt.xlabel('Observation number after given time steps')
    plt.ylabel('Sunspots scaled')
    plt.title('Actual and Predicted Values. The Red Line Separates The Training And Test Examples')
plot_result(trainY, testY, train_predict, test_predict)

生成了下面的图。

综合代码

下面给出的是本教程的全部代码。请在你的终端进行尝试，用不同的隐藏单元和时间步骤进行实验。你可以在网络中添加第二个SimpleRNN ，看看它的表现如何。你也可以使用scaler 对象将数据重新缩放到正常范围。

# Parameter split_percent defines the ratio of training examples
def get_train_test(url, split_percent=0.8):
    df = read_csv(url, usecols=[1], engine='python')
    data = np.array(df.values.astype('float32'))
    scaler = MinMaxScaler(feature_range=(0, 1))
    data = scaler.fit_transform(data).flatten()
    n = len(data)
    # Point for splitting data into train and test
    split = int(n*split_percent)
    train_data = data[range(split)]
    test_data = data[split:]
    return train_data, test_data, data

# Prepare the input X and target Y
def get_XY(dat, time_steps):
    Y_ind = np.arange(time_steps, len(dat), time_steps)
    Y = dat[Y_ind]
    rows_x = len(Y)
    X = dat[range(time_steps*rows_x)]
    X = np.reshape(X, (rows_x, time_steps, 1))    
    return X, Y

def create_RNN(hidden_units, dense_units, input_shape, activation):
    model = Sequential()
    model.add(SimpleRNN(hidden_units, input_shape=input_shape, activation=activation[0]))
    model.add(Dense(units=dense_units, activation=activation[1]))
    model.compile(loss='mean_squared_error', optimizer='adam')
    return model

def print_error(trainY, testY, train_predict, test_predict):    
    # Error of predictions
    train_rmse = math.sqrt(mean_squared_error(trainY, train_predict))
    test_rmse = math.sqrt(mean_squared_error(testY, test_predict))
    # Print RMSE
    print('Train RMSE: %.3f RMSE' % (train_rmse))
    print('Test RMSE: %.3f RMSE' % (test_rmse))    

# Plot the result
def plot_result(trainY, testY, train_predict, test_predict):
    actual = np.append(trainY, testY)
    predictions = np.append(train_predict, test_predict)
    rows = len(actual)
    plt.figure(figsize=(15, 6), dpi=80)
    plt.plot(range(rows), actual)
    plt.plot(range(rows), predictions)
    plt.axvline(x=len(trainY), color='r')
    plt.legend(['Actual', 'Predictions'])
    plt.xlabel('Observation number after given time steps')
    plt.ylabel('Sunspots scaled')
    plt.title('Actual and Predicted Values. The Red Line Separates The Training And Test Examples')

sunspots_url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/monthly-sunspots.csv'
time_steps = 12
train_data, test_data, data = get_train_test(sunspots_url)
trainX, trainY = get_XY(train_data, time_steps)
testX, testY = get_XY(test_data, time_steps)

# Create model and train
model = create_RNN(hidden_units=3, dense_units=1, input_shape=(time_steps,1), 
                   activation=['tanh', 'tanh'])
model.fit(trainX, trainY, epochs=20, batch_size=1, verbose=2)

# make predictions
train_predict = model.predict(trainX)
test_predict = model.predict(testX)

# Print error
print_error(trainY, testY, train_predict, test_predict)

#Plot result
plot_result(trainY, testY, train_predict, test_predict)

摘要

在本教程中，你发现了递归神经网络和它们的各种架构。

具体来说，你学到了。

  • RNNs的结构
  • RNN如何从以前的输入计算输出
  • 如何使用RNN实现一个用于时间序列预测的端到端系统
avatar
文章
阅读
粉丝