分组密码原理

一、流密码与分组密码

流密码

1.每次加密数据流的一位或一个字节。

2.例子：古典密码的Vigenere密码和Vernam密码。

3.出于实用的原因，位流必须以算法程序的方式实现，从而双方都可以产生具有密码学意义的位流。

分组密码

1.将一个明文组作为整体加密且通常得到的是与之等行的密文组。

2.典型分组大小是64位或128位。

可逆变换（非奇异变换）：每个明文分组唯一对应一个密文分组。

应用理想分组密码有着实际上的困难：

1.分组太小时，密码系统等价于传统代替密码；

2.从实现和运行的角度来看，采用大规模分组的任意可逆代替密码（即理想分组密码）不可行。 Feistel指出，我们所需要的是对理想分组密码体制的一种近似体制，它可以在容易实现不见得基础上逐步建立起来。Feistel建议使用乘积密码得概念来逼近理想分组密码。

乘积密码

在单个加密机制中依次使用两个或两个以上不同类型的基础密码（如：代换和置换），所得结果的密码强度将强于每个单个密码的强度。

本质：

开发一个分组密码，密钥长度为k位，分组长位n位，采用2的k次方个变换，而不是2的n的阶乘次方的逆变换。

特别的，Feistel建议使用这样的密码：这种密码交替地使用代替和置换。

代替：每个明文元素或元素组被唯一地替换为相应的密文元素或元素组；

置换：明文元素中的序列被替换为该序列的一个置换。也就是说，序列中没有元素被添加、删除或替换，但序列中元素出现的顺序改变了。

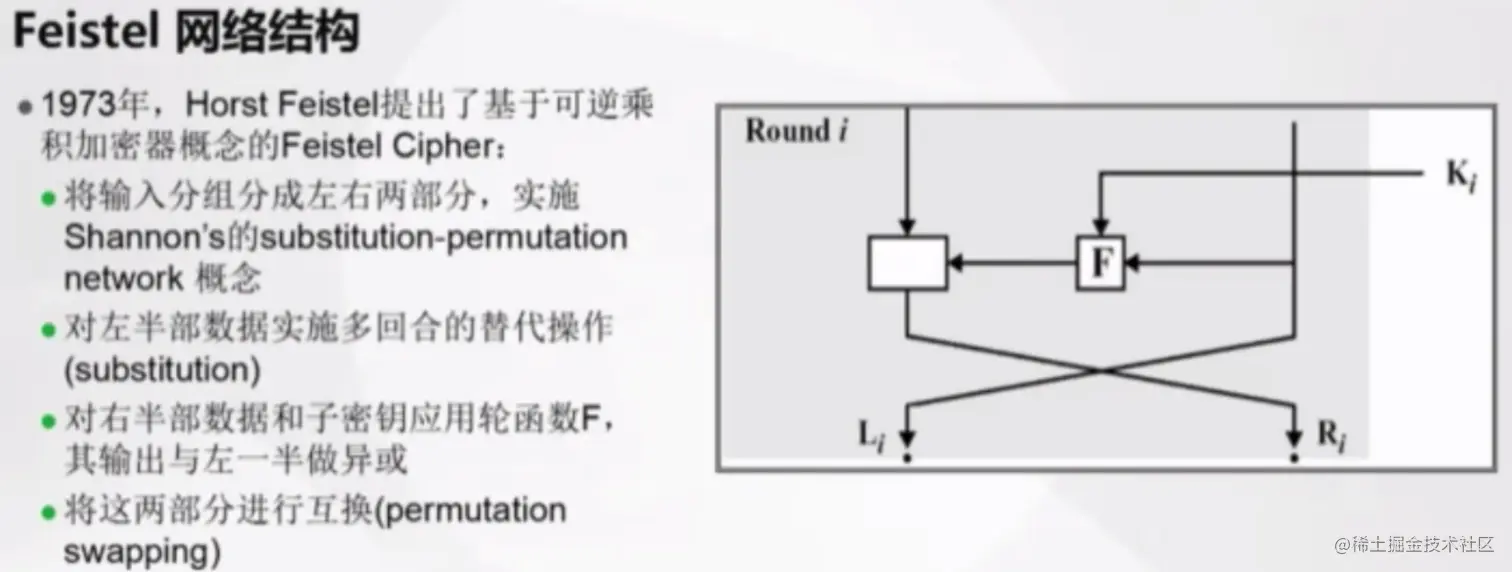
Feistel密码的解密过程与其加密过程实质是相同的。

以密文作为算法的输入，但是以相反的次序使用子密钥Ki,这就是说在第一轮用Kn,在第二轮用Kn-1,如此等等，直到在最后一轮使用K1。 注意：记住通式。

1.分组大小：分组越大意味着安全性越高（如果其他条件相同），但加密/解密速度也越慢。

2.密钥大小：密钥长度越长则安全性越高，但加密/解密速度也越慢。

3.循环次数：一个循环不能保证足够的安全性，而循环越多，则安全性较高。

4.子密钥产生算法：算法越复杂则密码分析就应该越困难。

5.Round函数：复杂性越高则抗击密码分析的能力就越强。

1.快速的软件加密/解密：在很多情况下，加密过程被以某种方式嵌入在应用程序或工具函数中以至于没法用硬件实现，因此，算法的执行速度就成为一个重要的考虑因素。

2.便于分析：如果算法能够简洁地解释清楚，那么就很容易通过分析算法而找到密码分析上地弱点，也就能够对其牢固程度有更大信心。