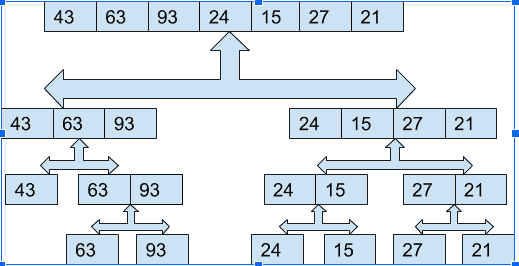
在合并排序 算法中,我们将数组递归地分成两半,直到每个子数组包含一个元素,然后我们以一种方式合并子数组,从而得到一个排序的数组。
C++合并排序
C++ 合并排序 是一种高效的、基于比较的算法,用于对一个数组或整数列表进行排序。合并排序不断地将列表分成相等的两半,直到它不能再被分割。根据定义,如果列表中只有一个元素,它就被排序了。然后,合并排序将较小的排序列表合并,保持新列表的排序。
这是 约翰-冯-诺伊曼在1945年发明的 "分割 与征服 " 算法。现在你可能会问什么是 "分割与征服 "方法。
C++中的合并排序 首先将一个数组分成相等的两半,然后以排序的方式将它们合并。你可以在本博客中查看泡沫排序和选择排序的例子。
这就像分而治之的方法。那么,让我们来 讨论一下分与合的方法 。
分割与合并法有以下三个任务:
- 将 问题划分为与原问题类似但规模较小的子问题。
- 递归地征服这些子问题。如果它们的大小较小,就直接解决它们。
- 将 这些解决方案合并为一个解决方案,这就是原始问题的答案。
让我们了解一下C++中的合并排序,然后写一个程序来演示一下。
分割与征服算法如何在合并排序中工作
排序问题:将 一个有 n个 元素 的序列 按非递减顺序排序。
分割:把 要排序 的n个元素序列分成两个子序列 , 每个子 序列有 n/2个元素。
征服: 使用合并排序对这两个子序列进行递归排序。
合并: 合并两个排序的子序列以产生排序后的答案。
自上而下的合并排序方法是一种使用递归机制的方法。它从顶部开始向下进行,每个递归轮流问同样的问题,如 "需要做什么来对数组进行排序?",答案是 "将一个数组分成两个,进行递归调用,然后合并结果。",直到到达数组树的底部。
例子
好吧,在看代码之前,先了解一下合并排序的模型;这将有助于你了解代码。
让我们考虑一个整数的列表。
| 43 | 63 | 93 | 24 | 15 | 27 | 21 |
所以,按照算法,我们首先需要把列表的长度(n)分成两部分,直到把它们分成一个节点。
所以在这里, n=7 现在 n/2=3。因此,第一部分将由3个整数组成,第二部分将由 7-3=4 部分组成。
需要注意的是。如果列表的大小是偶数,两边将被平分。但是对于ODD的情况,较小的尺寸将在左边,而较重要的将在右边。
因此,在 步骤1之后 , 列表将被分割成如下形式。
| 43 | 63 | 93 | 24 | 15 | 27 | 21 |
再像这样,我们将每个列表除以2,左边的 列表将出现在1+2中,右边的列表将出现在2+2部分。同样的事情会再次发生,直到它们都被分开。 所以,这里我们将看到除法后的最终列表。请看下图。
好的,在所有的除法操作完成后,我们将执行 征服(Conquer), 使用合并排序(merge Sort) 和 合并(Combine )对两个子序列进行递归排序,即 合并两个排序的子序列,产生排序的答案操作。
所以在这里,我们将看到每一步之后的结果是什么。
所以,这里发生的事情是......首先,它比较了两个子序列;例如,63和93被检查并在合并后以升序排列。同样地,27和21也被检查,然后在合并后以升序排列。
同样在第二步,43,63,93被检查并在合并后以升序放置。通过这种方式,我们得到了 最终的入围名单。
| 15 | 21 | 24 | 27 | 43 | 63 | 93 |
合并排序的伪代码
合并排序的伪代码如下。
procedure mergesort( var a as array )
if ( n == 1 ) return a
var l1 as array = a[0] ... a[n/2]
var l2 as array = a[n/2+1] ... a[n]
l1 = mergesort( l1 )
l2 = mergesort( l2 )
return merge( l1, l2 )
end procedure
procedure merge( var a as array, var b as array )
var c as array
while ( a and b have elements )
if ( a[0] > b[0] )
add b[0] to the end of c
remove b[0] from b
else
add a[0] to the end of c
remove a[0] from a
end if
end while
while ( a has elements )
add a[0] to the end of c
remove a[0] from a
end while
while ( b has elements )
add b[0] to the end of c
remove b[0] from b
end while
return c
end procedure
C++ 合并排序 程序
请看下面的mergesort.cpp文件。
#include<bits/stdc++.h>
using namespace std;
int Merge(int A[],int p, int q,int r)
{
int n1,n2,i,j,k;
//size of left array=n1
//size of right array=n2
n1=q-p+1;
n2=r-q;
int L[n1],R[n2];
//initializing the value of Left part to L[]
for(i=0;i<n1;i++)
{
L[i]=A[p+i];
}
//initializing the value of Right Part to R[]
for(j=0;j<n2;j++)
{
R[j]=A[q+j+1];
}
i=0,j=0;
//Comparing and merging them
//into new array in sorted order
for(k=p;i<n1&&j<n2;k++)
{
if(L[i]<R[j])
{
A[k]=L[i++];
}
else
{
A[k]=R[j++];
}
}
//If Left Array L[] has more elements than Right Array R[]
//then it will put all the
// reamining elements of L[] into A[]
while(i<n1)
{
A[k++]=L[i++];
}
//If Right Array R[] has more elements than Left Array L[]
//then it will put all the
// reamining elements of L[] into A[]
while(j<n2)
{
A[k++]=R[j++];
}
}
//This is Divide Part
//This part will Divide the array into
//Sub array and then will Merge them
//by calling Merge()
int MergeSort(int A[],int p,int r)
{
int q;
if(p<r)
{
q=(p+r)/2;
MergeSort(A,p,q);
MergeSort(A,q+1,r);
Merge(A,p,q,r);
}
}
int main()
{
int n;
cout<<"Enter size of the Array: ";
cin>>n;
int A[n],i;
cout<<"Enter array values:\n";
for(i=0;i<n;i++)
cin>>A[i];
//Calling the MergeSort()
//First we are passing the array
//the start index that is 0
//and the size of the array n
MergeSort(A,0,n-1);
cout<<"The Sorted List is\n";
for(i=0;i<n;i++)
{
cout<<A[i]<<" ";
}
return 0;
}
其输出结果如下。
合并排序的时间复杂度
合并排序的运行时间 T**(n)** 。
- 分割:计算中间需要Θ(1)
- 征服:解决2个子问题需要2T(n/2)
- 合并:合并 n个 元素需要Θ(n)
- 总的时间复杂度如下。
T(n) = Θ(1)
if n = 1T(n) = 2T(n/2) + Θ(n)
if n > 1
T(n)= 2 T(n/2) + n
= 2 ((n/2)log(n/2) + (n/2)) + n
= n (log(n/2)) + 2n
= n log n – n + 2n
= n log n + n
= O(n log n )
上述递归可以用递归树或主方法来解决。然而,它属于主方法的情况二,重复的解决方法是O(n log n)。
合并排序的时间复杂度在所有3种情况下(最差、平均和最佳)都是O(n log n),因为合并排序将数组分成两半,合并两半需要线性时间。
最坏情况下的时间复杂度为Ο(n log n),它是最受尊敬的算法之一。
合并排序的应用
- 合并排序有助于在O(nLogn)时间内对链接列表进行排序。
- 它被用于反转计数问题中。
- 我们可以在外部排序中使用它。
本教程到此结束。