从 pyTroch 开始聊起自动求导 (2)持续创作，加速成长！这是我参与「掘金日新计划 · 6 月更文挑战」的第31天

持续创作，加速成长！这是我参与「掘金日新计划 · 6 月更文挑战」的第31天，点击查看活动详情

torch.autograd 是推动训练的自动求导引擎，通过今天分享将会对 autograd 是如何推动模型训练有一个概念上理解。

神经网络可以看做嵌套函数集合，那么什么是嵌套函数呢？ $f(g(x))$ ,嵌套函数通常一个嵌套在非线性激活函数的线性函数，学习的是线性函数的权重和偏置。这些权重和偏置参数都是用 tensor 来表示。

训练过程通常包含两个阶段

前向传播: 在前向传播中，数据经过一层层函数得出一个对数据关心方面的预测
反向传播:

链式法则

理解链式法则对于理解反向传播很重要，我们从最最简单的网络讲起吧，这个网络足够简单，每一层只有一个神经元

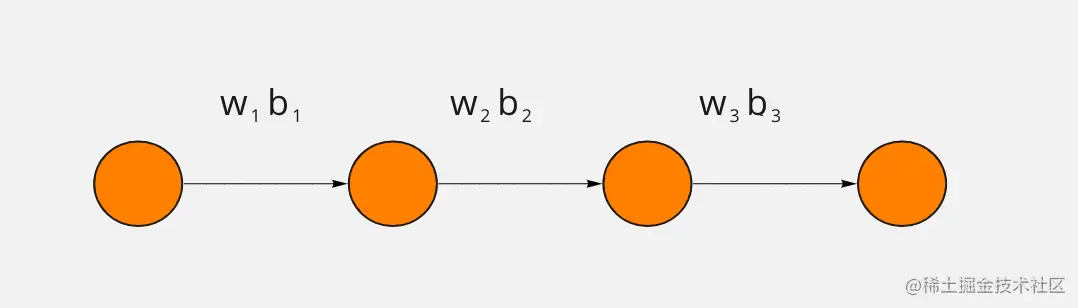
图上这个神经网络的参数就是包括 3 个权重和 3 个偏置，每一层提供一个权重和一个偏置。

我们的目标是理解损失函数对于这些变量的敏感程度，然后根据这些变量对损失函数影响程度，来调节这些变量，让损失函数降低得最快

接下来先看最后两个神经元，这里上标表示神经元层数，一共有 $L$ 层，随意最后表示为 $a^{(L)}$ ，前一层神经元输出可以表示为 $a^{(L-1)}$ ，这里上标表示变量所位于神经网络层数。

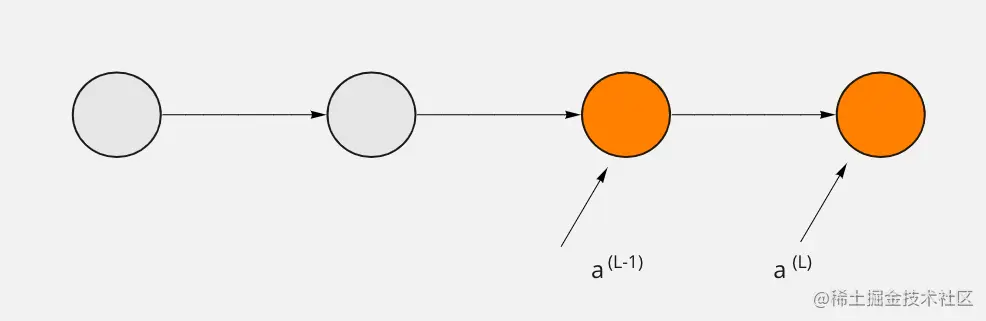
给定一个训练样本把这个最终层激活值要接近的目标叫做 y，这里假设是一个而分类问题，那么 y 取值可能是 0 或者是 1 来表示两个不同的类别。

那么在这个简单网络中，对于单个训练样本的损失函数就可以表示为 $(a^{(L)} - y)^2$ ,这是平法损失函数，用 $C_0$ 表示损失函数，这里下标是表示样本。

接下里我们看一看，这里上一层输出 $a^{(L-1)}$ 经过一个线性变换为 $w^{(L)}a^{(L-1)} + b^{(L)}$ , 这里我们可以用 $z^{(L)}$ 来表示 $w^{(L)}a^{(L-1)} + b^{(L)}$ 那么在对线性变化的结果进行一次非线性操作， $a^{(L)} = \sigma(z^{(L)})$

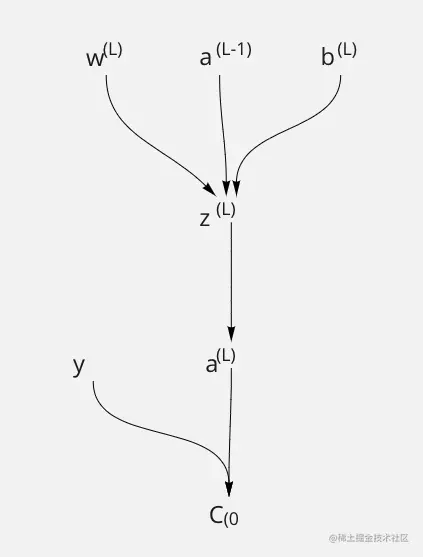
接下来我们我们来看 $w^{(L)}$ 是对 $C_0$ 进行影响的，可以通过图，就是要理解权重 $w^{(L)}$ 微小变化会给 $C$ 带来多少变化，可以用 $\frac{\partial C}{\partial w}$ ,

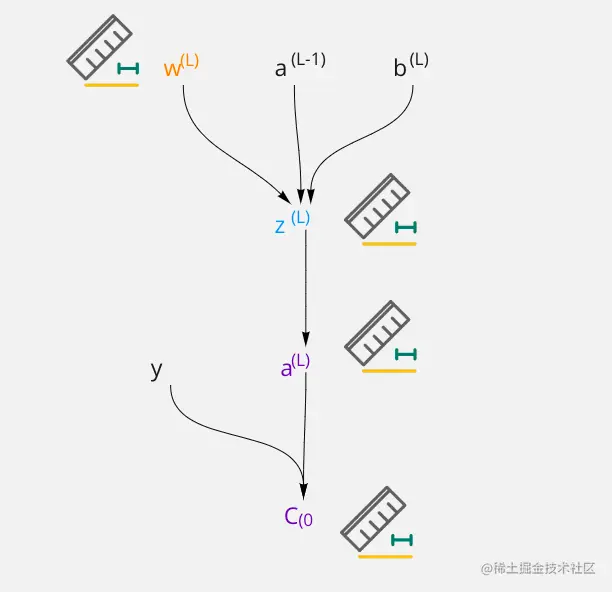
通过这张图不难理解， $w^{(L)}$ 通过对于 $z^{(L)}$ 影响，然后一路从 $z^{(L)}$ 经过 $a^{(L)}$ 影响到 $C_{0}$ 的，这就是链式法则。

\frac{\partial C_0}{w^{(L)}} = \frac{\partial z^{(L)}}{w^{(L)}}\frac{\partial a^{(L)}}{\partial z^{(L)}}\frac{\partial C_0}{a ^{(L)}}

接下来就可以一项一项进行求导，我们先把这些式子都列出了，以便进行对比

C_0 = (a^{(L)} - y)^2\\ z^{(L)} = w^{(L)}a^{(L-1)} + b^{(L)}\\ a^{(L)} = \sigma(z^{(L)}

$C_0$ 关于 $a^{(L)}$ 的导数就是 $2(a^{(L)} - y)$

\frac{\partial C_0}{\partial a^{(L)}} = 2 (a^{(L)} - y)

这也就意味着导数的大小跟网络最终输出 $a^{(L)}$ 和目标结果的差成正比，如果网络的输出差别很大，即便 $w$ 稍稍变一点损失函数也会有很大的改变。

$a^(L)$ 对 $z^(L)$ 求导就是求 sigmoid 的导数，可以表示为

\frac{\partial a^{(L)}}{\partial z^{(L)}} = \sigma^{\prime }(z^{(L)})

或就你选择的非线性激活函数

\frac{\partial z^{(L)}}{\partial w^{(L)}} = a^{(L-1)}

\frac{\partial C_0}{w^{(L)}} = a^{(L-1)}\sigma^{\prime }(z^{(L)})2 (a^{(L)} - y)

基于类似方法，我们可以计算 $\frac{\partial C_0}{b^{(L)}}$ 和 $\frac{\partial C_0}{a^{(L-1)}}$

\frac{\partial C_0}{b^{(L)}} = 1 \times \sigma^{\prime }(z^{(L)})2 (a^{(L)} - y)

\frac{\partial C_0}{a^{(L-1)}} = w^{(L)}\sigma^{\prime }(z^{(L)})2 (a^{(L)} - y)

而 $z^{(L)}$ 对 $w^{(L)}$ 求导，导数为 $a^{(L-1)}$ ,从公式来 $\partial w$ 对损失函数影响程度取决于其上一层的输出 $a^{(L-1)}$ ，这样进一步验证了一同激活的神经元关联在一起(neurons fire together wire together)。

计算损失函数是是一个批次多个样本进行求平均来计算的如下

\frac{\partial C}{w^{(L)}} = \frac{1}{n} \sum_{k=0}^{n-1} \frac{\partial C_k}{w^{(L)}}

梯度是由方向的所以 $\nabla C = \begin{bmatrix} \frac{\partial C}{\partial w^{(1)}} \\ \frac{\partial C}{\partial w^{(1)}} \\ \vdots\\ \frac{\partial C}{\partial w^{(L)}} \\ \frac{\partial C}{\partial w^{(L)}} \\ \end{bmatrix}$

而真实的神经网络会比这个例子复杂的多、一个网络会有多个层，每一个层会有多个神经元，这时候下标就派上用场了。

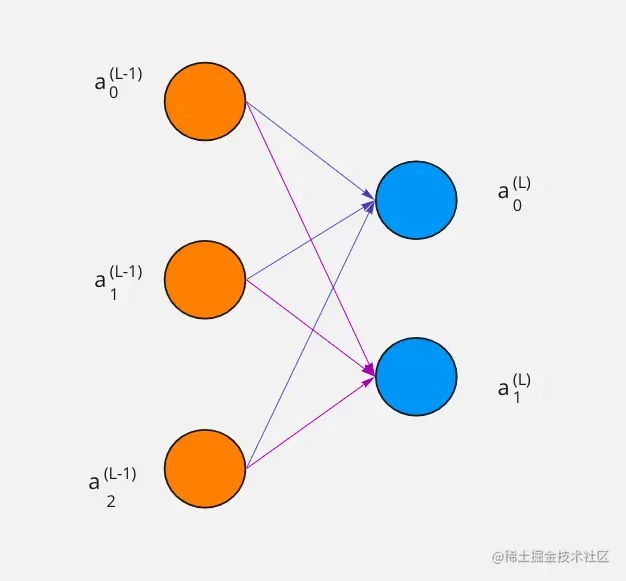
用下标来表示某一个层的某一个神经元

C_0 = \sum_{j=1}^{n_L - 1} \left(a_j^{(L)} - y_j\right)^2

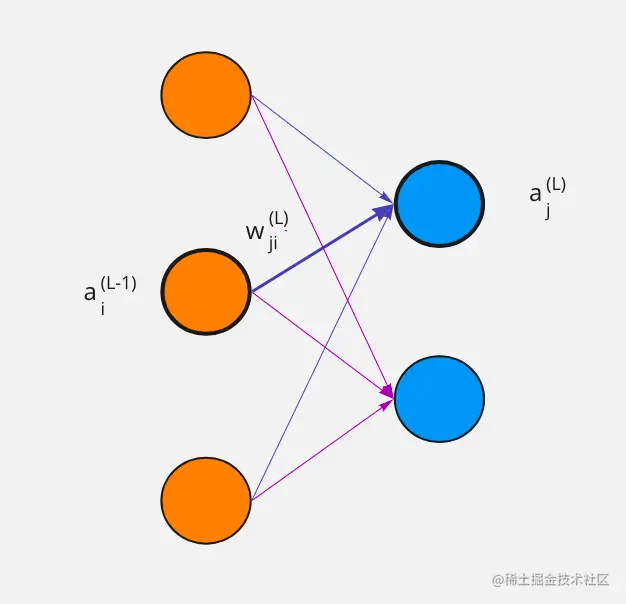
在 L 层中下标 $j$ 表示第 L 激活值，而 $i$ 表示 L-1 第 $i$ 激活值，他们之前权重用 $w_{ji}^{(L)}$ 这里 $j$ 和 $i$ 的顺序有些奇怪，原因是是矩阵相乘。

C_0 = \sum_{j=1}^{n_L - 1} \left(a_j^{(L)} - y_j\right)^2

z_j^{(L)} = w_{j0}^{L} a_0^{(L-1)} + w_{j1}^{L} a_1^{(L-1)} + w_{j2}^{L} a_2^{(L-1)}

现在当前 $j$ 激活函数值是由上一层所有元素加权求和得到 $z_j^{(L)}$ 然后对其 $\sigma(z_j^{(L)})$ 就得到了激活值

a_j^{(L)} = \sigma(z_j^{(L)})

\frac{\partial C_0}{w^{(L)}_{jk}} = \sum_{j=0}^{n_L - 1} \frac{\partial z^{(L)}_j}{w^{(L)}_{jk}}\frac{\partial a^{(L)}_j}{\partial z^{(L)}_j}\frac{\partial C_0}{a ^{(L)}_j}

现在的方程式和之前每层只有一个神经元的时候本质是一样的