在本教程中,你将学习如何在R中进行Brown-Forsythe检验。这个检验非常好,因为你可以用它来检验方差的同质性假设,这对于方差分析(ANOVA)等非常重要。
帖子的概要
本帖的结构如下。首先,我们先回答与这个测试有关的几个问题。其次,我们了解布朗-福尔赛测试的假设。接下来是最重要的部分,也许是在R中进行Brown-Forsythe测试的5个步骤,当然,现在也可以用更少的步骤来完成。下面是如何用三个步骤进行测试,其中一个步骤涉及安装一个软件包。
布朗-福赛斯测试的三个步骤
什么是Brown-Forsythe测试?
在本节中,你将得到一些关于这个测试是什么的简单细节。如前所述,只要我们需要测试等方差的假设,就会使用布朗-福赛测试。此外,它是对列文氏检验的修改,但布朗-福赛斯检验使用中位数,而不是平均值(列文氏)。如前所述,该检验被认为是一种稳健的检验,是基于每组内与组内中位数的绝对差异。布朗-福赛特检验是替代巴特利特检验的一个合适的等方差检验方法,因为它对缺乏正态性和不平等的样本量并不敏感。更多关于布朗-福尔赛检验的信息,请参见这篇文章或文章末尾的资源。
我如何在R中进行布朗-福尔赛检验?
你可以使用R软件包onewaytests中的bf.function()来进行布朗-福赛斯测试。例如,bf.function(DV ~ IV, data=dataFrame)将成功地在数据帧dataFrame中执行因变量DV和组IV的检验。
在下一节中,你将了解布朗-福赛特检验的假设。知道假设后,对结果的解释就更容易了。
测试的假说
当使用R进行布朗-福赛尔测试时,我们要测试以下两个假设。
- H0:群体方差是相等的。
- HA:人口变异数不相等。
因此,正如我们在浏览例子时看到的,我们不想拒绝无效假设(H0)。 在下一节中,你将得到一个可以用来进行测试的R软件包的简要介绍。
R语言中的布朗-福尔赛测试
现在,如你所知,R是一种开源语言。这意味着可能有更多的包使我们有可能在R中进行Brown-Forsythe测试,但在这篇文章中,我们将只使用一个包。
Onewaytests
Onewaytests更专注于进行单程测试。使用这个包,我们可以进行单因素方差分析、韦尔奇异方差F检验、韦尔奇异方差F检验与修剪后的均值和温索化方差、布朗-福尔赛检验、亚历山大-戈文检验、詹姆斯二阶检验等等。当然,函数bf.test()是本博文的兴趣所在。
如何在R中进行Brown-Forsythe检验。X个简单步骤
现在我们已经准备好在R中进行布朗-福赛特测试了。
步骤1:安装onewaytests包
现在,你可能已经知道如何安装R包,但这里是我们如何安装onewaytests包。
install.packages("onewaytests")
Code language: R (r)
注意,在第三步中,我们还将使用dplyr对数据进行汇总,以计算每组的方差。此外,我们将使用readxl包导入示例数据集。这两个包都是Tidyverse包的一部分。因此,为了完全跟上这篇文章,请同时安装Tidyverse包(当然,也可以只安装dplyr)。
install.packages(c("onewaytests", "tidyverse"))
Code language: R (r)
上面的代码将同时安装onewaytests和Tidyverse。另一方面,如果你只想安装dplyr和readxl(用于读取Excel文件),你可以去掉 "tidyverse",加入 "dplyr "和 "readxl"。只要按照上面的语法操作就可以了。现在,Tidyverse附带了很多优秀的软件包。例如,你可以用dplyr来重命名列,计算列中出现的次数,用stringr来合并R中的两列。
在下一步,我们将使用readxl包来导入示例数据集。
第二步:将数据导入R。
下面是我们如何使用readxl包在R中读取Excel文件。
library(readxl)
dataFrame <- read_excel('brown-forsythe-test-in-R-example-data.xlsx')
Code language: R (r)
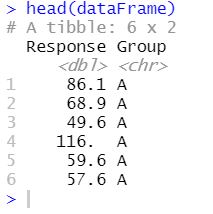
首先,在进入下一步之前,我们可以先探索一下数据框架。例如,我们可以得到前6行:
head(dataFrame)
Code language: R (r)
我们可以看到,这个例子的数据中只有两个变量。首先,我们有 "组 "这一列,在这一列中我们可以找到不同的治疗组("A"、"B "和 "C")。如果我们想看看是什么数据类型,可以输入这个:
str(dataFrame)
现在,我们看到Group是因子,Response是数字(即num)。在下一节中,我们将直观地看到每组中Response的方差。
当然,如果你的数据是以这两种数据类型中的任何一种存储的,也可以在R中把矩阵转换成数据框,或者把列表转换成数据框。
第三步:通过可视化和计算差异来探索数据
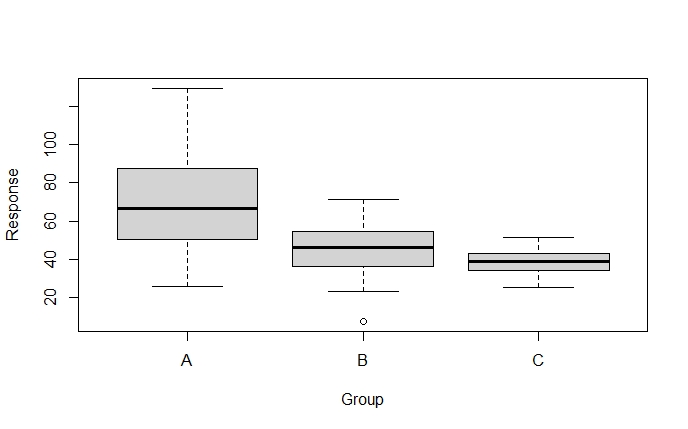
正如你可能知道的,在R中,有许多不同的方法来可视化数据。在这里,我们将使用boxplot()函数,它将给我们一个想法,即各组的变异是否相等。下面是如何创建一个boxplot。
boxplot(Response ~ Group, data = dataFrame)
Code language: R (r)
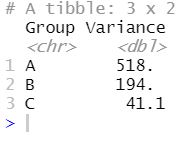
当检查boxplots时,看起来不同治疗组的方差肯定是不同的。我们也可以用dplyr计算方差,按组计算。
library(dplyr)
dataFrame %>%
group_by(Group) %>%
summarize(Variance=var(Response))
Code language: R (r)
方差
现在,从上面的图片来看,我们在不同的治疗组中也有不同的变异。然而,在下一步,我们将使用bf.test()函数进行Brown-Forsythe检验,检验方差相等的无效假设。
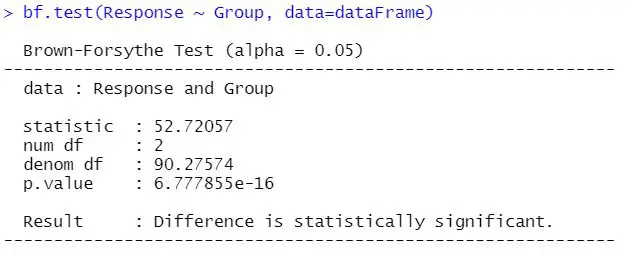
第4步:进行Brown-Forsythe检验
下面是你如何在R中进行布朗-福赛测试。
library(onewaytests)
bf.test(Response ~ Group, data = dataFrame)
Code language: R (r)
在上面的代码块中,我们使用bf.test()函数(onewaytests包)来进行Brown-Forsythe检验。注意我们是如何使用一个公式作为第一个参数的。这与你在R中进行方差分析时使用的公式完全相同。
在下一节,我们将学习如何解释测试的结果。
第5步:解释结果
解释Brown-Forsythe检验是非常简单的。只要记住我们有一个无效假设,即各组的变异量相等。因此,如果p值低于0.05,我们就拒绝无效假设,并得出结论,数据不符合变异性同质性假设。
在我们的例子中,无效假设被拒绝。然而,如果p值高于0.05,我们就不会拒绝无效假设。在这种情况下,我们可以安全地继续进行例如单因素方差分析。
如果你的数据违反了同质性假设,但却是正态分布,你应该继续使用韦尔奇方差分析,这也可以在R中进行。
总结
在这篇博文中,你已经学会了如何在R中进行Brown-Forsythe方差均匀性检验,具体来说,你已经逐步学会了如何进行这个检验。首先,你学会了如何在R中安装一个能够进行布朗-福尔赛检验的R包。其次,你导入了示例数据,第三,探索了数据。最后,你学会了如何使用bf.test()函数进行检验。 现在可能还有其他包和函数使我们能够进行这种等差检验。如果你知道有什么其他的包或函数可以让我们在R中进行Brown-Forsythe检验,请在下面留言。当然,也欢迎你建议我在今后的博文中应该涉及哪些内容,纠正我博文中的错误,或者只是让我知道你是否觉得这篇文章有用。也就是说,我鼓励你在下面发表评论!