持续创作,加速成长!这是我参与「掘金日新计划 · 6 月更文挑战」的第25天,点击查看活动详情
红黑树的特性
- 每个节点或者是红色的,或者是黑色的;
- 根节点是黑色的;
- 每个叶子结点(最后的空节点)是黑色的;
- 如果一个节点是红色的,那么他的孩子都是黑色的;
- 从任意一个节点到叶子节点经过的黑色节点是一样的。
2-3树
绝对平衡的一种数据结构。
基本性质
节点可以存放一个元素或者两个元素
添加节点
新节点永远不会添加到空子树中去,(新节点的添加不会自己新建一个子树)他只会和最后一个子树融合
- 对于一个空的2-3树,添加的元素作为根节点。
2. 添加37。
因为37比42小,所以应该添加到42的左子树上,但是此时2-3树42没有左子树,所以将37和42进行融合,成为一个节点。
3. 添加12
因为12比37小,所以应该添加到37的左子树,但是37的左子树为空,所以和37节点进行融合。暂时形成可以存储三个元素的节点。
2-3树最多只能存储2个元素,所以该节点要进行分裂。
4. 添加18
按上述道理添加到12的右子树,但是12节点的右子树为空,所以和12节点进行融合。
5. 添加6
按照上述推论和12节点融合,暂时形成有三个元素的节点。
1. 进行分裂
2. 当前2-3树不是绝对平衡的树,分裂之后6,12,18形成新的树,12作为当前子树的根节点,要和他的双亲进行融合。
融合后,回复平衡。
6. 添加11
7. 添加5
1.
2.
3.
4.
红黑树与2-3树
因为普通的二叉搜索树只能存储两个指针域,所以,想让二叉树的节点存储三个指针域可以将两个二叉树的节点看成是一个2-3树的节点,如图:
等价于
为了便于区分,可以用红色节点表示该节点何双亲表示同一个节点。
所以一颗2-3树转换为红黑树后如图:
等价于
- 向红黑树中添加节点
2-3树种添加新节点都是和最后一个找到的叶子节点进行融合,之后可能会采取分裂的措施,所以类比2-3树后红黑树新添加的节点都应该为红色节点。
/**
* 用于表示红黑树的颜色
*/
private static final boolean RED = true;
private static final boolean BLACK = false;
/**
* 红黑树节点定义
*/
private class Node {
public K key;
public V value;
public boolean color;
public Node left, right;
public Node(K key, V value) {
this.key = key;
this.value = value;
left = null;
right = null;
//新添加的节点都要融合到叶子节点上,所以新建的节点都为红色
color = RED;
}
}
- 添加42节点
- 新建的节点都为红色,因为此时的红色树为空,所以该节点为根节点;
2. 根据红黑树的特点:根节点为黑色,所以要变色
- 添加37节点
- 根据二分搜索树的特性,37应该作为42 的左子树。
假设根节点的元素为37,添加的元素为42
- 根据二分搜索树的规则,42应该作为37的右子树
- 但是现在的红黑树并不满足红黑树的特性,要进行左旋,变色进行调整。
红黑树左旋
左旋的形式和二叉平衡树方法一致; 旋转后节点颜色变换为x的颜色和node节点颜色保持一致(为了向上兼容);
node节点的颜色变为红色。
/**
* 红黑树左旋操作
* @param node 要旋转的二叉树的根节点
* @return 当前二叉树的根节点
*
* node x
* / \ / \
* T1 x -----------> node T3
* / \ / \
* T2 T3 T1 T2
*/
private Node leftRotate(Node node){
Node x = node.right;
node.right = x.left;
x.left = node;
x.color = node.color;
node.color = RED;
return x;
}
【注意】 该左旋操作并不会保证红黑树的特性,当前红黑树的根节点会随着递归到上一层进行进一步处理,该左旋操作的目的是为了让这两个节点成为2-3树种的3节点。
- 向红黑树种添加66节点 根据二叉搜索树的规则,新节点66应该作为42的右子树进行加插入。
等价于2-3树种的可以存储3个元素的节点。
2-3树处理该情况采用分裂,根节点和他上面的双亲节点进行融合,即,如图:
对应于红黑树
- 当前子树的根节点的左右子树都为黑色。
2.根节点变为红色和他的双亲进行融合。
这一过程称为颜色翻转
如果向刚才的红黑树中添加的元素只为12
根据二叉搜索树的特性,应该添加到37的左孩子处。
等价于2-3树种的可以存储3个元素的节点。
2-3树处理该情况采用分裂,根节点和他上面的双亲节点进行融合,即,如图:
对应红黑树的处理:
- 右旋转
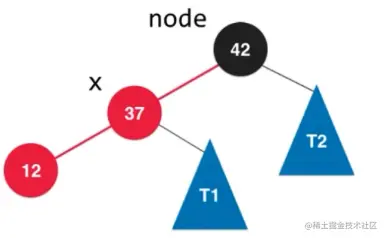
- 变色 当前子树的新的根节点的颜色和之前该子树根节点颜色一致。
node节点的颜色变为红色。
变色完成后,此时红黑树对应的2-3树如图:
/**
* 红黑树右旋操作
* @param node 要旋转的二叉树的根节点
* @return 当前二叉树的根节点
*
* node x
* / \ / \
* x T2 -----------> y node
* / \ / \
* y T1 T1 T2
*/
private Node rightRotate(Node node){
Node x = node.left;
node.left = x.right;
x.right = node;
x.color = node.color;
node.color = RED;
return x;
}
- 进行颜色翻转
向红黑树种添加节点为40的元素 根据二叉搜索树的特性,40应该成为37的右孩子。
- 左旋
- 右旋
- 变色
- 颜色翻转
总结一下添加二叉树的情况
通过上图可以看出,红黑树添加节点的操作可以看成是一条逻辑链,只有在最复杂的情况下,每一步都要执行,在添加节点的时候,只需要判断每一步是否需要执行即可。
维护的时机添加节点之后,向上进行回溯进行维护。
完整代码:
public class RBTree<K extends Comparable<K>, V> {
/**
* 用于表示红黑树的颜色
*/
private static final boolean RED = true;
private static final boolean BLACK = false;
/**
* 红黑树节点定义
*/
private class Node {
public K key;
public V value;
public boolean color;
public Node left, right;
Node(K key, V value) {
this.key = key;
this.value = value;
left = null;
right = null;
//新添加的节点都要融合到叶子节点上,所以新建的节点都为红色
color = RED;
}
}
private Node root;
private int size;
public int getSize() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
public boolean isRed(Node node) {
if (node == null) {
return BLACK;
}
return node.color;
}
public RBTree() {
root = null;
size = 0;
}
/**
* 红黑树左旋操作
* @param node 要旋转的二叉树的根节点
* @return 当前二叉树的根节点
*
* node x
* / \ / \
* T1 x -----------> node T3
* / \ / \
* T2 T3 T1 T2
*/
private Node leftRotate(Node node){
Node x = node.right;
node.right = x.left;
x.left = node;
x.color = node.color;
node.color = RED;
return x;
}
/**
* 红黑树右旋操作
* @param node 要旋转的二叉树的根节点
* @return 当前二叉树的根节点
*
* node x
* / \ / \
* x T2 -----------> y node
* / \ / \
* y T1 T1 T2
*/
private Node rightRotate(Node node){
Node x = node.left;
node.left = x.right;
x.right = node;
x.color = node.color;
node.color = RED;
return x;
}
/**
* 颜色翻转
* @param node 要翻转的根节点
*/
private void flipColors(Node node){
node.color = RED;
node.left.color = BLACK;
node.right.color = BLACK;
}
/**
* 向红黑树中添加新节点
* @param key key
* @param value value
*/
public void add(K key, V value) {
root = add(root, key, value);
//最终根节点为黑色节点
root.color = BLACK;
}
private Node add(Node node, K key, V value) {
if (node == null) {
size++;
return new Node(key, value);
}
if (key.compareTo(node.key) < 0) {
node.left = add(node.left, key, value);
} else if (key.compareTo(node.key) > 0) {
node.right = add(node.right, key, value);
} else {
node.value = value;
}
//维护红黑树的过程
if(isRed(node.right)&&!isRed(node.left)){
node = leftRotate(node);
}
if(isRed(node.left)&&isRed(node.left.left)){
node = rightRotate(node);
}
if(isRed(node.left)&&isRed(node.right)){
flipColors(node);
}
return node;
}
}